10.9. Каноническое разложение непериодической случайной функции

В п. 10.6 было введено следующее гармоническое разложение стационарной случайной функции (10.2)

Это разложение справедливо для периодических функций с периодом 2T. В приведенном в 10.7 примере в качестве периода принимался удвоенный интервал корреляции. Такой выбор, конечно, произволен. Если, например, вдвое увеличить период, то вдвое увеличится и число гармоник, а дисперсии их амплитуд уменьшатся в два раза.

Для того чтобы распространить приведенные соотношения на случай непериодической функции, устремим период к бесконечности, тогда и число гармоник увеличится до бесконечности, а их амплитуды станут бесконечно малыми. В итоге получим формулы интегрального преобразования Фурье.

(10. 5)

Здесь

S() носит название спектральной плотности, или короче, спектра. (Спектр - латинское слово, означающее представление, образ).

10.10. Каноническое разложение корреляционной функции и дисперсии непериодической случайной функции

Каноническое разложение корреляционной функции для периодической случайной функции, полученное в п. 10.6 имеет вид

Совершим и здесь такой же предельный переход, как в предыдущем параграфе, после чего получим пару преобразований Фурье:

(10.6)

Полагая  = 0, получим каноническое разложение дисперсии

Отсюда становится ясен смысл функции G() - это спектр дисперсии стационарной случайной функции.

10.11. Связь между спектром стационарной случайной функции и спектром ее корреляционной функции

Найдем эту связь для эргодической случайной функции, но результат будет иметь более универсальный характер. Для корреляционной функции имеем

Введем временно функцию X_T(t), совпадающую с x(t) в интервале от -T до T, и равную нулю вне интервала, тогда получим

Преобразуем это выражение с использованием (10.5).

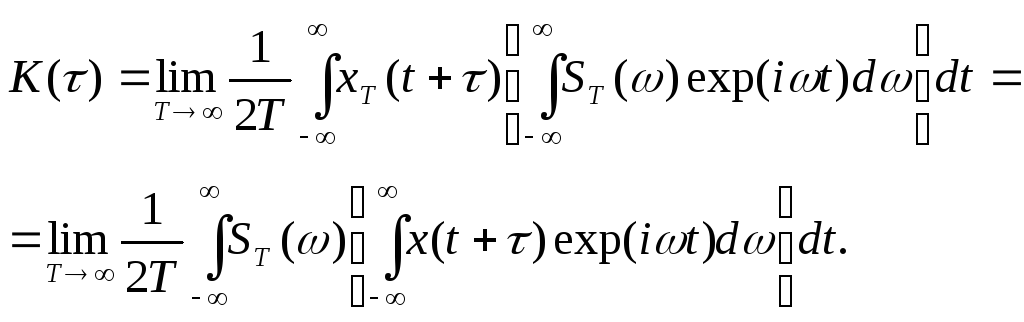
Помножим и разделим внутренний интеграл на

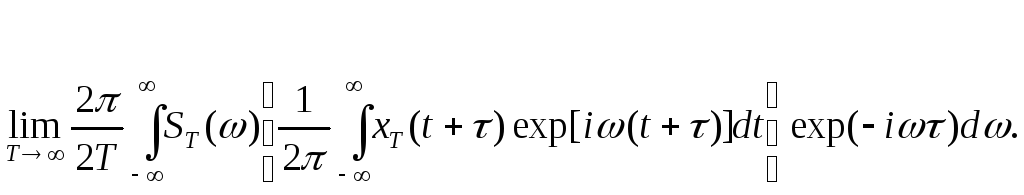
При условии, что x_T(t+) - функция действительная - внутренний интеграл представляет собой функцию комплексно сопряженную с S_T(), следовательно

Используя формулу Эйлера, учитывая, что - функция - четная и применяя правила вычисления интегралов от четных и нечетных функций в симметричных пределах, находим

Сравнивая полученное выражение с (10.6), изменяя порядок интегрирования и перехода к пределу и вводя для спектра корреляционной функции новое обозначение G(), находим искомую взаимозависимость