10.6. Каноническое разложение стационарной случайной функции

Если случайная функция стационарна, то координатными функциями являются косинус и синус:

(10.2)

где U_j и V_j - центрированные некоррелированные случайные величины с попарно равными дисперсиями D(U_j) = D(V_j) = D_j.

Такое разложение называется спектральным. Ему соответствует разложение в ряд Фурье по косинусам корреляционной функции:

(10.3)

Отсюда для дисперсии при  = 0

(10.4)

В справедливости приведенных формул легко убедиться прямой проверкой, если учесть, что

M(U_kV_i) = M(U_kV_j) = M(U_kU_j) = M(V_kV_j) = 0 (при k  j).

В теории стационарных случайных функций доказывается, что справедливо и обратное утверждение: если возможно разложение корреляционной функции в ряд (10.3), то случайная функция может быть представлена каноническим разложением (10.2), где коэффициенты разложения U_k и V_k (k = 1,2,...) имеют дисперсии, равные коэффициентам ряда (10.3). Это открывает способ имитационного моделирования стационарных случайных функций по заданным математическому ожиданию и корреляционной функции.

10.7. Модель ветровой нагрузки

На этом примере рассмотрим алгоритм имитации стационарного процесса.

Рис. 10.4.

Пульсации скоростного напора ветра, как показывают исследования [10], представляют собой нормальные стационарные случайные процессы Q(t), корреляционные функции которых по экспериментальным данным для различных районов земного шара близки между собой. На рис. 10.4 приведены нормированные корреляционные функции, полученные на Нефтяных камнях (район Баку). Как следует из рисунка, корреляционная функция может быть аппроксимирована экспонентой:

Эта аппроксимация не имеет нулевой производной при  = 0 и конечного интервала корреляции. Введем интервал корреляции _k, связав его с величиной  так, чтобы обеспечить желаемую степень точности:

Теперь

Разложим эту функцию в ряд Фурье по косинусам, считая, что период функции равен 2_k:

где коэффициенты разложения

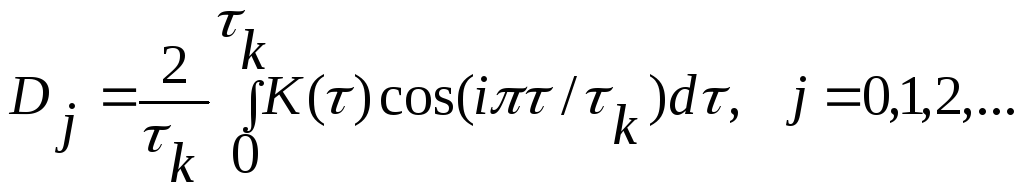
Так как корреляционная функция в действительности не является периодической, ее среднее равно нулю (D₀ = 0). Для остальных коэффициентов находим

Здесь принято, что exp(-_k) = 0.

Каноническое разложение для ветровой нагрузки имеет вид

Дисперсии коэффициентов U_j и V_j равны коэфициентам D_j.

Для определения числа слагаемых m, которое целесообразно удерживать в разложении, положимk = 5 и вычислим отношениеD₁/D_m:

При m = 20 это отношение равно 100.

10.8. Модель транспортной нагрузки [10]

Построение канонического разложения для продольного профиля дороги аналогично приему, использованному в предыдущем параграфе. Отличие состоит в том, что случайная функция имеет в качестве аргумента продольную координату, а корреляционная функция аппроксимируется экспоненциально-косинусной зависимостью

Значение дисперсии D_x зависит от класса дороги.

Для перехода к процессу, возникающему при движении транспорта по дороге случайного профиля, следует координату l заменить на время  по соотношению, учитывающему скорость движения V:

 = l/V.

После преобразования коэффициенты _v и _v принимают значения из диапазонов

 _v= 0.01...0.1 1/с;

 _v= 0.02...0.15 1/с.