2.4.1 Тесты проверки ²случайности²

На практике обычно применяют два теста проверки ²случайности²: тест проверки серий и тест проверки частот и пар.

Тест проверки серий предусматривает разбиение случайных цифр в исследуемой последовательности на элементы двух родов - первого и второго.

Серией называется любой отрезок последовательности цифр, состоящий из следующих друг за другом элементов одного и того же рода. Например, если в последовательности цифр

e₁, e₂, ¼,e_k e_{k + 1}, e_{k + 2}, ¼ ,e_{k +} e_{k ++ 1}, e_k++2, ¼ ,e_s

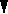
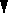
серия 1-го серия 2-го серия 1-го

рода длины k рода длины рода длиныs - k -

e₁ ¹ e₂ ¹ ¼ ¹ e_k ¹ e_{k + 1}, e_{k + 1} = e_{k + 2} = ¼ = e_{k +} и e_{k +}¹ e_{k ++ 1} ¹ ¼ ¹ e_s, то цифры e₁, e₂, ¼ ,e_k образуют серию первого рода длины k, цифры e_{k + 1}, e_{k + 2}, ¼ ,e_{k +} образуют серию второго рода длины и цифрыe_{k ++ 1}, e_{k++ 2}, ¼ ,e_s также обра-зуют серию первого рода длины s - k -.Иногда для удобства элементы серий первого рода обозначают знаками ²-² ( минус ), а второго рода - знаками ²+² ( плюс ). В этом случае рассматриваемая последовательность будет иметь такой вид:

- - ¼ - + + ¼ + - - ¼ -

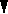
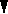
k минусов плюсов s - k -минусов

Подсчитаем количество серий второго рода длины в последовательности псевдослучайных цифр e₁, e₂, ¼ ,e_N. Пусть = 1, 2, ¼, m и - количество серий второго рода с ³ m + 1 ( они объединяются в одну группу ). Обозначим общее количество серий через

= ++¼ + +.

Величина сm степенями свободы вычисляется по формуле:

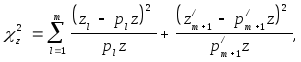( 11 )

где

Если, с заданным уровнем значимости b, значение попадает в доверитель-ный интервал, то тест проверки серий удовлетворяется.

В практике встречается также другая разновидность теста проверки серий, когда к элементам серий первого рода относят цифры, меньшие 0.5, а к элемен-там серий второго рода - не меньшие 0.5.

При достаточно большом объеме выборки e₁, e₂, ¼,e_N ( практически при N ³ 20 ) и уровне значимости b = 0.95 нижний предел общего числа серий равен:

( 12 )

а нижний предел числа серий элементов первого и второгородов равен:

( 13 )

Максимальная длина серий не должна быть больше, чем

( 14 )

2.4.2 Тест проверки равномерности закона распределения

Данный тест строится на основе применения критерия согласия . Пусть имеется выборкаe₁, e₂, ¼,e_N псевдослучайных чисел в интервале ( 0, 1 ). Интервал ( 0, 1 ) изменения случайной величины e разбивается на m интервалов х_j, j = 1, 2, ¼, m, очевидно, что х_m = 1, а нижняя граница первого интервала равна нулю. Обычно принимают m = 10 ¸ 20.

Далее производится определение вероятности p_j попадания случайной вели-чины e в j-й интервал. Для равномерного на интервале ( 0, 1 ) закона распределения p_j = x_j - x_j-1. Затем определяется величина , j = 1, 2, ¼ ,m - число попаданий случайной величины e в j-й интервал и подсчитывается величина

распределенная по закону с ( m-1 ) степенью свободы. По заданному уровню значимости b путем решения уравнений ( 9 ) и ( 10 ) ( с помощью таблицы, приведенной в приложении А ) можно определить нижнюю и верхнююграницы доверительного интервала. Если подсчитанное значениене попадает в доверительный интервал, то гипотезу о равномерном законе распределения случайной величины e следует отвергнуть.

Дополнительно можно подсчитать эмпирическое математическое ожидание

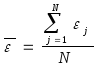( 15 )

и эмпирическую дисперсию

( 16 )

и сравнить их с теоретическими значениями соответственно 0.5 и 1 / 12.

Для математического ожидания можно для заданного уровня значимости b определить также доверительный интервал:

( 17 )

где d определяется из уравнения:

2Ф=b. ( 18 )

Значения интеграла вероятностей Ф ( х ) приведены в приложении Б.

Полезно бывает сравнить также теоретическую функцию распределения и теоретическую плотность распределения случайной величины e с экспери-ментально полученными функцией распределения и гистограммой частот.

Известно, что для случайной величины, равномерно распределенной на интер-вале ( 0, 1 ):

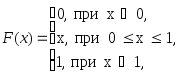
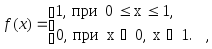
По известной выборке из N значений случайной величины e эксперимен-тальная функция распределения определяется следующим образом:

где равно количеству значенийe < х.

Гистограмма частот, являющаяся аналогом плотности распределения, строится следующим образом. Весь интервал ( х_min, х_max ) от наименьшего значения х_min до наибольшего значения х_max полученной выборки случайной величины разбивается на q равных промежутков длины h. Затем определяется число значений n_i выборки, попавших в i-ый промежуток, после чего для каждого 1 £ i £ q строится прямоугольник с основанием на i-ом промежутке и высотой n_i / h. Полученный чертеж называется гистограммой частот или просто гистограммой. Отметим, что при таком построении площадь i-го прямоугольника равна h × ( n_i / h ) = n_i, т.е. числу значений случайной величины, попавших в i-ый промежуток, а площадь всей гистограммы равна объему выборки.