12.6.2. Компенсация систематической погрешности в процессе измерения.

В практике измерений применяется несколько методов, позволяющих за счет некоторого усложнения процедуры измерений получить результат измерения свободным от систематической погрешности. К ним относятся метод замещения, метод противопоставления и метод компенсации погрешности по знаку.

12.6.2.1.Метод замещения.

Этот метод дает наиболее полное решение задачи компенсации постоянной систематической погрешности и представляет собой разновидность метода сравнения. Сравнение производится путем замены измеряемой величины известной величиной и так, чтобы воздействием известной величины привести средство измерения в то состояние, которое оно имело при воздействии измеряемой величины.

Пример. Взвешивание на пружинных весах, у которых имеется постоянная систематическая погрешность (из-за смещения шкалы, например). Взвешивание производится в два приема. Вначале на чашу весов помещают взвешиваемое тело массой Мх и отмечают положение указателя. Затем взвешиваемое тело замещают гирями такой массы Мо, чтобы вновь добиться прежнего отклонения указателя. Разность между Мх и Мо -. погрешность и ее следует учесть введением поправки. Поправка равна погрешности, взятой с обратным знаком, или в единицах измеряемой величины

12.6.2.2. Метод противопоставления.

Рассмотри данный метод на следующем примере:

При взвешивании на рычажных весах условие равновесия весов равенство произведений массы на длину плеча весов. Если длины плеч одинаковы, то масса груза и гирь одинаковы. Если длины плеч различны (из-за технологического разброса длин плеч при их изготовлении, например), то при взвешивании каждый раз возникает систематическая погрешность.

Для исключения этой погрешности взвешивание производится в два этапа. Сначала взвешивают груз уравновешивая весы гирями (Мо1). Затем взвешиваемый груз перемещают на ту чашу весов, где прежде были гири и вновь уравновешивают весы (новой массой гирь Мо2)). Теперь исключив из полученных равенств отношение плеч, найдем

Как видно из формулы, длины плеч не входят в окончательный результат взвешивания.

12.6.2.3.Метод компенсации погрешности по знаку.

Этот метод также предусматривает проведение измерения в два этапа выполняемых так, чтобы постоянная систематическая погрешность входила в показания средства измерения на каждом этапе с разными знаками. За результат измерения принимают полусумму показаний — систематические погрешности при этом взаимно компенсируются.

12.6.2.4. Суммирование систематических погрешностей.

Независимо от того, к какому виду относится измерение, является ли оно прямым, косвенным совместным или совокупным, систематическая погрешность результата; измерения оценивается, как правило, по ее известным составляющим.

Поскольку в каждом конкретном случае каждая систематическая составляющая получает конкретную реализацию (она либо постоянная, либо известен закон ее изменения), то результирующая, суммарная систематическая погрешность представляет собой алгебраическую сумму составляющих:

12.6.3. Случайные погрешности.

12.6.3.1. Вероятностное описание результатов и погрешностей.

Когда при проведении с одинаковой тщательностью и в одинаковых условиях повторных наблюдений одной и той же постоянной величины получаем результаты, отличающиеся друг от друга, это свидетельствует о наличии в них случайных погрешностей. Каждая такая погрешность возникает вследствие одновременного воздействия на результат наблюдения многих случайных возмущений, и сама является случайной величиной. В этом случае предсказать результат отдельного наблюдения и исправить его введением поправки невозможно. Можно лишь с определенной долей уверенности утверждать, что истинное значение измеряемой величины находится в пределах разброса результатов наблюдений от Хmin до Хmax, где Хmin и Хmax — соответственно, нижняя и верхняя границы разброса. Однако остается неясным, какова вероятность появления того или иного значения погрешности, какое из множества лежащих в этой области значений величины принять за результат измерения и какими показателями охарактеризовать случайную погрешность результата. Для ответа на эти вопросы требуется принципиально иной, чем при анализе систематических погрешностей, подход. Подход этот основывается на рассмотрении результатов наблюдений, результатов измерений и случайных погрешностей как случайных величин. Методы теории вероятностей, математической статистики позволяют установить вероятностные (статистические) закономерности появления случайных погрешностей и на основании этих закономерностей дать количественные оценки результата измерения и его случайной погрешности.

Для характеристики свойств случайной величины в теории вероятностей используют понятие закона распределения вероятностей случайной величины. Различают две формы описания закона распределения: интегральную и дифференциальную. В метрологии преимущественно используется дифференциальная форма — закон распределения плотности вероятностей случайной величины.

Рассмотрим формирование дифференциального закона на примере измерений с многократными наблюдениями. Пусть произведено n последовательных наблюдений одной и той же величины х и получена группа наблюдений х1, х2, х3, ..., хn. Каждое из значений х1 содержит ту или иную случайную погрешность. Расположим результаты наблюдений в порядке их возрастания, от Хmin до Хmax и найдем размах ряда L=Хmax - Хmin. Разделим размах ряда на k равных интервалов l=L/k, подсчитаем количество наблюдений попадающих в каждый интервал. Изобразим полученные результаты графически, нанеся на оси абсцисс значения физической величины и обозначив границы интервалов, а по оси ординат — относительную частоту попаданий n_k /n. Построив на диаграмме прямоугольники, основанием которых является ширина интервалов, а высотой n_k /n, получим гистограмму, дающую представление о плотности распределения результатов наблюдений в данном опыте. На рис. 4 показана полученная в одном из опытов гистограмма, построенная на основании результатов 50 наблюдений, сгруппированных в таблицу.

В данном опыте в первый и последующие интервалы попадает соответственно 0,1; 0,2; 0,36; 0,22 и 0,12 от общего количества наблюдений; при этом очевидно, что сумма этих чисел равна единице.

Если распределение случайной величины х статистически устойчиво, то можно ожидать, что при повторных сериях наблюдений той же величины, в тех же условиях, относительные частоты попаданий в каждый интервал будут близки к первоначальным. Это означает, что единожды построив гистограмму, при последующих сериях наблюдений можно с определенной долей уверенности заранее предсказать распределение результатов наблюдений по интервалам. Приняв общую площадь, ограниченную контуром гистограммы и осью абсцисс, за единицу, 50 = 1, относительную частоту попаданий результатов наблюдений в тот или иной интервал можно определить как отношение площади соответствующего прямоугольника шириной l к общей площади.

При бесконечном увеличении числа наблюдений n  и бесконечном уменьшении ширины интервалов l  ступенчатая кривая, огибующая гистограмму, перейдет в плавную кривую f(х) (рис.), называемую кривой плотности распределения вероятностей случайной величины, а уравнение, описывающее ее, — дифференциальным законом распределения. Кривая плотности распределения вероятностей всегда неотрицательна и подчинена условию нормирования в виде:

неопределенный интеграл от f(х) по dx равен 1.

Рис. 4. Гистограмма

Рис.5. Кривая плотности распределения вероятностей

Закон распределения дает полную формацию о свойствах случайной величины и позволяет ответить на поставленные вопросы о результате измерения и его случайной погрешности. Если известен дифференциальный закон распределения случайной величины f(х), то вероятность Р ее попадания в интервал от Х₁, до Х₂ равна интегралу Х₁, - Х₂ от f(х) по dx

.

Графически эта вероятность выражается отношением площади, лежащей под кривой f(х) в интервале от Х₁, до Х₂ к общей площади, ограниченной кривой распределения.

Кроме непрерывных случайных величин в метрологической практике встречаются и дискретные случайные величины. Пример распределения дискретной случайной величины приведен на рис. 6.

Рис.6. Распределение случайной величины.

Для описания частных свойств случайной величины используют числовые характеристики распределений. В качестве числовых характеристик выступают моменты случайных величин: начальные и центральные. Все они представляют собой некоторые средние значения; причем, если усредняются величины, считываемые от начала координат, моменты называются начальными, а если от центра закона распределения — то центральными.

Начальный момент k-го порядка определяется формулами

где p_i— вероятность появления дискретной величины.

Здесь и ниже первая формула относится к непрерывным, а вторая к дискретным случайным величинам.

Из начальных моментов наибольший интерес представляет математическое ожидание случайной величины (к = 1),

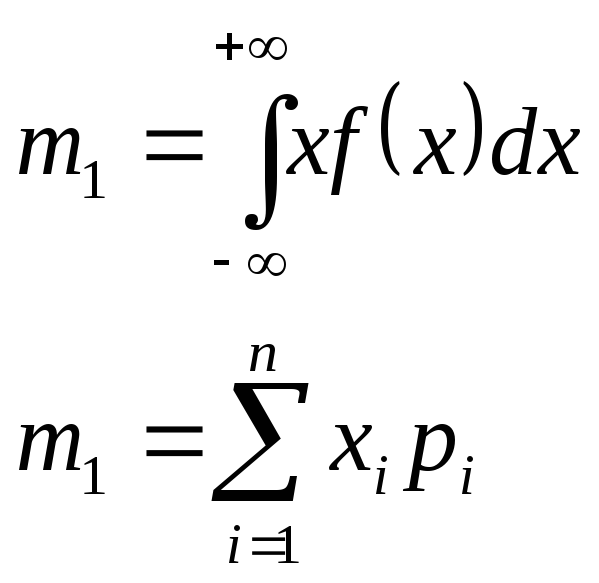
Центральные моменты к-го порядка рассчитываются по формулам

Из центральных моментов особенно важную роль играет второй момент (к = 2), дисперсия случайной величины D

Дисперсия случайной величины характеризует рассеяние отдельных значений. Дисперсия имеет размерность квадрата случайной величины и выражает как бы мощность рассеяния относительно постоянной составляющей. Однако чаще пользуются положительным корнем квадратным из дисперсии — средним квадратическим отклонением (СКО), которое имеет размерность самой случайной величины.