39.Дифференциальные уравнения с разделяющимися переменными. Однородные дифференциальные уравнения первого порядка.

Р(х,у)dх+Q(х,у) dу=0

Если в уравнении правая часть раскладывается на множители, каждый из которых зависимый от одного аргумента , то уравнение называется Дифференциальным уравнением с разделяющимися переменными.

Задача Каши для диф.ур.

Найти решение уравнения удовлетворяющему условию y(x)=y₀.

Уравнение с разделяющимися переменными называется уравнение вида:

f₁(x)f₂(y)dx+g₁(x)g₂(y)dy=0

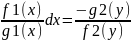dy далее интегрируем обе части.

Однородные дифференциальные уравнения первого порядка

Функция F(х,у) называется однородной измерения n если, при любом t выполняется тождество: F(tx,ty)=tⁿF(x,y)

Дифференциальным уравнением Р(х,у)dх+Q(х,у) dу=0 называется однородным если P и Q однородные функции одного и того же измерения n.

P(tx,ty)=tⁿP(x,y)

Q(tx,ty)=tⁿQ(x,y)

40.Линейные дифференциальные уравнения. Уравнения Бернулли.

Уравнения Бернулли называется уравнение вида:

Уравнения Бернулли может быть сведено к линейному уравнению

Уравнения Бернулли можно сразу решить подстановкой

Линейные дифференциальные уравнения- если неизвестная функция и все ее производные входят в уравнение.

Линейные дифференциальные уравнения бывают нескольких видов:

1)Уравнение с переменными коэффициентами

2)Уравнение первого порядка

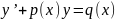
3) Уравнение первого порядка с переменными коэффициентами

4) Уравнение первого порядка с постоянными коэффициентами

41.Дифференциальные уравнения в полных дифференциалах.

Дифференциальные уравнения в полных дифференциалах называется уравнение вида: Р(х,у)dх+Q(х,у) dу=0

Левая часть которого есть полный дифференциал некоторой функции U=U(x,y)

Р(х,у)=U^’x

Q(х,у)= U^’y

Условия совместности U^’xу =U^’yх

Необходимые и достаточные условия

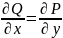
42,Дифференциальные уравнения высших порядков. Уравнения, допускающие понижение порядка.

1)Уравнение вида: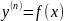

Решение этого уравнения находится n-кратным интегрированием

и т.д.

2) Уравнение вида: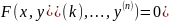

Уравнение решаем с помощью замены 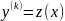при этом понижается порядок на к-1 т.е. отсюда находим z(x) а затем находим у^к-кратным интегралом.

3) Уравнение вида: решается с помощью замены dz/dy=z(с точкой вверху)

4) Уравнение вида: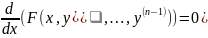 решение 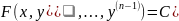и заменой у=UV

5) Уравнение вида : однородное относительно ф-ции у и ее производных

43.Линейные однородные дифференциальные уравнения высших порядков с постоянными коэффициентами.

Линейным однородным уравнением  -го порядка с постоянными коэффициентами называется уравнение вида

(1)

где коэффициенты   – некоторые действительные числа. Для нахождения частных решении уравнения (1) составляют характеристическое уравнение (2)

которое получается из уравнения (1) заменой в нем производных искомой функции соответствующими степенями k, причем сама функция заменяется единицей. Уравнение (2) является уравнением n степени и имеет n корней.

Тогда общее решение дифференциального уравнения (1) строится в зависимости от характера корней уравнения (2):

1.каждому действительному простому корню k в общем решении соответствует слагаемое вида  ;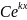

2.каждому действительному корню кратности   в общем решении соответствует слагаемое вида  ;

3.каждой паре комплексных сопряженных простых корней   и   в общем решении соответствует слагаемое вида 

4.каждой паре комплексных сопряженных корней   и  кратности   в общем решении соответствует слагаемое вида