
- •Функции нескольких переменных.
- •8.Производная по направлению, градиент
- •Как связаны производная по направлению и градиент дифференцируемой функции ? Чему равна производная по направлению, перпендикулярному градиенту?
- •Дайте определение градиента функции в точке . Докажите, что в направлении градиента происходит наиболее быстрый рост функции. Чему равна скорость этого роста?
- •Имеет ли функция локальный экстремум в точке ?
- •Сформулируйте достаточные условия локального экстремума функции в некоторой точке.
- •Каков алгоритм нахождения наибольшего и наименьшего значений функции в замкнутой ограниченной области?
- •58. Найдите наибольшее и наименьшее значения функции в круге .
- •Интегральное исчисление
- •12.Первообразная и неопределенный интеграл
- •Дайте определение первообразной. Докажите, что если и – первообразные функции на интервале , то на этом интервале , где – некоторая постоянная.
- •Сформулируйте свойства неопределенного интеграла. Докажите, что .
- •Известно, что первообразная функции , первообразная функции и . Какова связь между функциями и ? Дайте обоснованный ответ.
- •Пусть , , . Найдите .
- •Докажите формулу интегрирования по частям для неопределенного интеграла.
- •13.Определенный интеграл
- •Дайте определение функции , интегрируемой на отрезке . Докажите, исходя из определения, что постоянная функция интегрируема на любом отрезке.
- •Пусть , и . Найдите
- •Докажите, что если функция непрерывна на отрезке , то функция , , является ее первообразной на этом отрезке.
- •Используя свойство интеграла с переменным верхним пределом, докажите формулу Ньютона - Лейбница.
- •Дайте определение несобственного интеграла от неограниченной функции. При каких значениях сходится интеграл ?
- •15.Сходимость и сумма числового ряда
- •Дайте определения числового ряда и его суммы. Найдите, исходя из определения, сумму ряда при .
- •Сформулируйте и докажите необходимое условие сходимости числового ряда. Приведите пример расходящегося ряда, для которого это условие выполнено.
- •16.Числовые ряды с неотрицательными членами
- •Сформулируйте и докажите признак Даламбера для числовых рядов с положительными членами.
- •Сформулируйте признак Даламбера в предельной форме. Приведите пример сходящегося ряда с положительными членами, к которому этот признак применим.
- •Дайте определение гармонического ряда. Докажите, что гармонический ряд расходится.
- •17. Знакочередующиеся числовые ряды
- •Сформулируйте признак Лейбница для знакочередующихся числовых рядов. Приведите пример знакочередующегося ряда, сходящегося условно.
Функции нескольких переменных.
6.Предел и непрерывность функции
Дайте определение предела функции двух переменных в точке. Докажите, что функция
 не имеет предела в точке
не имеет предела в точке
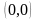
Пусть
{Аk}
– последовательность точек в Rn.
Точка А, принадлежащая Rn,
наз-ся пределом п-ти точек {Аk},
если любая окрестность точки А содержит
в себе все члены п-ти, начиная с некоторого
достаточно большого номера N.
То есть для всякого k
> N
точка Аk
принадлежит к этой окрестности.

Будет ли функция
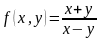 непрерывна в точке
непрерывна в точке
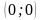 .
Дайте обоснованный ответ.
.
Дайте обоснованный ответ.
Функция u=f(M) называется непрерывной в точке А, если предел этой функции существует и равен значению функции в этой точке: limf(M)=f(A) MA
7.Частные производные, дифференцируемость, дифференциал
Дайте определение частной производной функции
 по переменной
по переменной
 ,
в точке
,
в точке
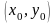 .
Найдите
.
Найдите
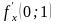 ,
если
,
если
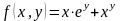 .
.
Частной производной по у функции z=f(x;y) называется предел отношений приращения ∆хz к приращению ∆х, при ∆х→0.
Zَx=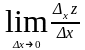 =lim(x0+∆х
; y0)-f(x0
;y0)/∆х,
у=const.
=lim(x0+∆х
; y0)-f(x0
;y0)/∆х,
у=const.
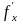 =
=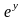 +
+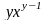
=е
Дайте определение частной производной функции по
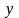 в точке
.
Найдите
в точке
.
Найдите
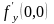 ,
если
,
если
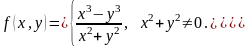
Частной производной по у функции z=f(x;y) называется предел отношений приращения ∆yz к приращению ∆у, при ∆у→0.
Zَx=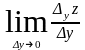 =lim(x0
; y0+∆y)-f(x0
;y0)/∆y,
x=const
=lim(x0
; y0+∆y)-f(x0
;y0)/∆y,
x=const
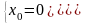
Дайте определение дифференцируемости функции в точке. Докажите, что если функция дифференцируема в точке , то она непрерывна в этой точке.
Функция
z=f(x;y)
называется дифференцируемой
в точке (x0,y0),
если ее полное приращение можно
представить в виде
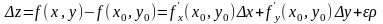
Если функция дифференцируема в точке, то она непрерывна в этой точке.
Достаточное
условие дифференцируемости функции m
переменных: Пусть функция f(![]() )
определена в некоторой окрестности
точки
)
определена в некоторой окрестности
точки
![]() .
Пусть у функции в этой окрестности
существуют непрерывные частые производные
по всем переменным, тогда функция f
дифференцируема в этой точке.
.
Пусть у функции в этой окрестности
существуют непрерывные частые производные
по всем переменным, тогда функция f
дифференцируема в этой точке.
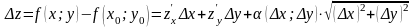 ,
где
,
где
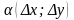 - б.м. ф-ция при
- б.м. ф-ция при
 .
.

=> ф-ция z=f(x,y) непрерывна в точке (х0;y0).
8.Производная по направлению, градиент
Как связаны производная по направлению и градиент дифференцируемой функции ? Чему равна производная по направлению, перпендикулярному градиенту?
Пусть
вектор l – произвольное направление,
которое образует с Ох угол α, а с Оу угол
β. Тогда их косинусы – направляющие
косинусы l.
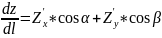 .
Градиент – вектор, координаты которого
являются значениями частной производной
в произвольной точке M
по каждой переменной.
.
Градиент – вектор, координаты которого
являются значениями частной производной
в произвольной точке M
по каждой переменной.
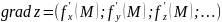 .
Он указывает направление наибыстрейшего
роста. Связаны они тем, что значение
.
Он указывает направление наибыстрейшего
роста. Связаны они тем, что значение
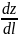 (или производная ф-ции по направлению)
является скалярным произведением
направляющего вектора на градиент. Так
как произведение ортогональных векторов
равно нулю, то производная по направлению,
перпендикулярному градиенту, также
равна 0.
(или производная ф-ции по направлению)
является скалярным произведением
направляющего вектора на градиент. Так
как произведение ортогональных векторов
равно нулю, то производная по направлению,
перпендикулярному градиенту, также
равна 0.
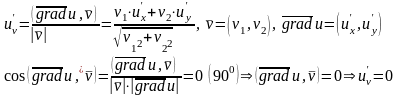
Дайте определение градиента функции в точке . Докажите, что в направлении градиента происходит наиболее быстрый рост функции. Чему равна скорость этого роста?
Градиентом
ф-ции z=
f(x,y)
в точке M(x,y)
называется вектор, координаты которого
равны соответствующим частным производным
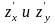 ,
взятым в точке M(x,y).
,
взятым в точке M(x,y).
Градиент указывает направление наискорейшего роста функции, а максимальная скорость равна модулю градиента.
По
определению скалярного произведения
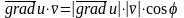 .
Учитывая, что
.
Учитывая, что
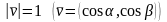 .
Из последнего следует, что производная
по направлению имеет наибольшую величину
при
.
Из последнего следует, что производная
по направлению имеет наибольшую величину
при
 ,
то есть когда направление вектора
,
то есть когда направление вектора
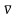 совпадает
с направлением
совпадает
с направлением
 .
Скорость роста равна модулю градиента.
.
Скорость роста равна модулю градиента.
9.Локальный экстремум
Дайте определение локального экстремума функции двух переменных. Является ли равенство нулю частных производных функции в некоторой точке достаточным условием ее локального экстремума в этой точке?
Точка
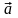 называется
точкой локального максимума
(минимума)
ф-ции
называется
точкой локального максимума
(минимума)
ф-ции
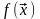 ,если
существует такая
,если
существует такая
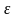 -окрестность,
-окрестность,
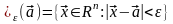 точки
точки
 в которой для любой точки
в которой для любой точки
 -
выполняется неравенство
-
выполняется неравенство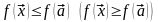
1)Для того, чтобы дифференцируемая ф-ция имела локальный экстремум в точке , необходимо, чтобы все ее частные производные первого порядка в этой точке были равны 0.
2)для того чтобы дифференцируемая функция имела локальный экстремум в точке а, необходимо, чтобы определитель вида f’’xx f’’xy был больше 0.
f’’xy f’’yy
