
- •Функции одной переменной
- •1.Предел последовательности
- •Дайте определение предела последовательности. Докажите, исходя из определения, что .
- •Докажите единственность предела сходящейся последовательности.
- •Докажите ограниченность сходящейся последовательности. Приведите пример ограниченной последовательности, не имеющей предела.
- •Существует ли ? Ответ обоснуйте.
- •Дайте определение функции, непрерывной в точке. Найдите значение , при котором функция является непрерывной в точке .
- •Дайте определение точки разрыва функции. Приведите примеры функций, для которых является: а) точкой разрыва I рода со скачком, равным 2; б) точкой разрыва II рода.
- •Сформулируйте теорему о существовании нуля непрерывной функции. Используя эту теорему, докажите, что уравнение имеет корень на отрезке .
- •Функция определена следующим образом . А) Существует ли ? б) Будет ли функция непрерывной в точке ? Дайте обоснованные ответы.
- •На рисунке изображен график функции .
- •Следует ли из существования производной функции в точке ее непрерывность в этой точке? Ответ обоснуйте.
- •Докажите теорему о производной суммы двух функций.
- •Докажите теорему о производной произведения двух функций.
- •На рисунке изображен график производной функции .
- •Функция такова, что для всех действительных значений , и . Какой из представленных графиков может быть графиком функции ?
Функции одной переменной
1.Предел последовательности
Дайте определение предела последовательности. Докажите, исходя из определения, что .
Число
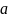 называется пределом
последовательности
называется пределом
последовательности
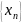 ,
если для любого положительного числа
ε существует такой номер
,
если для любого положительного числа
ε существует такой номер
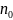 (зависящий от выбранного ε), начиная с
которого все члены последовательности
отличаются от
по модулю меньше, чем на ε:
(зависящий от выбранного ε), начиная с
которого все члены последовательности
отличаются от
по модулю меньше, чем на ε:
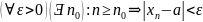
Имеем
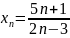 .
.
Взяв
произвольное
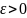 ,
составим неравенство
,
составим неравенство
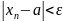 и выясним, для каких n
оно справедливо. Подставим в это
неравенство
и решим его относительно n.
и выясним, для каких n
оно справедливо. Подставим в это
неравенство
и решим его относительно n.
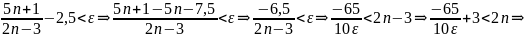
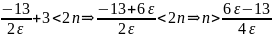
Т.о.,
приняв за
ближайшее к
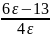 справа натуральное число, будем иметь
справа натуральное число, будем иметь
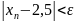 для всех
для всех
 ,
что означает справедливость равенства
,
что означает справедливость равенства
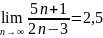
Докажите единственность предела сходящейся последовательности.
Теорема: Сходящаяся последовательность имеет только один предел.
Доказательство: (от противного)
Пусть
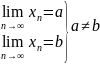
Выберем столь малые окрестности a и b, чтобы они не имели общих точек.
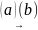
Т.к.
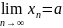 ,
то все
,
то все
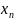 ,
начиная с некоторого номера
,
начиная с некоторого номера
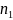 попадут в выбранную окрестность
попадут в выбранную окрестность
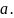
Т.к.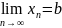 ,
то все
,
начиная с некоторого номера
,
то все
,
начиная с некоторого номера
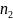 попадут в выбранную окрестность
попадут в выбранную окрестность .
.
Пусть
 .
Тогда
(все
)
должны принадлежать обеим окрестностям,
что невозможно, т.к. они пересекаются.
Возникает противоречие. Следовательно,
существует только один предел сходящейся
последовательности.
.
Тогда
(все
)
должны принадлежать обеим окрестностям,
что невозможно, т.к. они пересекаются.
Возникает противоречие. Следовательно,
существует только один предел сходящейся
последовательности.
Докажите ограниченность сходящейся последовательности. Приведите пример ограниченной последовательности, не имеющей предела.
Множество
чисел X называется ограниченным,
если существует
такой отрезок
 числовой оси, который содержит все
числа из X.
Или (что эквивалентно): множество X
ограничено, если существует такое
числовой оси, который содержит все
числа из X.
Или (что эквивалентно): множество X
ограничено, если существует такое
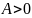 ,
что для всех чисел
,
что для всех чисел
 из X имеем
из X имеем
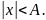
Доказательство второго свойства пределов:
Пусть
.
Положим
 и найдем номер
,
начиная с которого
и найдем номер
,
начиная с которого
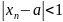 ,
т.е.
,
т.е.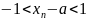 для
.
для
.
Отсюда
следует
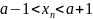 для всех
для всех
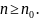 Заменим отрезок
Заменим отрезок
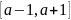 таким (быть может большим) отрезком
таким (быть может большим) отрезком
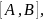 чтобы в него попали не только числа
,
,
но и все числа
чтобы в него попали не только числа
,
,
но и все числа
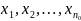 .
Тогда будем иметь
.
Тогда будем иметь
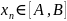 для всех
для всех
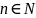 ,
что означает ограниченность множества
.
,
что означает ограниченность множества
.
Пример огр п-ти без предела: Xn=(-1)n, т.е Xn={-1; 1; -1; 1….}
Дайте определение последовательности, ограниченной сверху. Может ли предел последовательности, ограниченной сверху числом 5, быть равным: а) 4,99; б) 5,01? Ответ обоснуйте.
Последовательность
называется ограниченной
сверху, если
существует такое
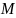 (м), что любой элемент
удовлетворяет неравенству
(м), что любой элемент
удовлетворяет неравенству
 .
.
Число 4,99 может быть пределом данной ограниченной последовательности, т.к.

Аналогично, 5,01 не может быть пределом, т.к.
 .
.
Что можно сказать о пределе произведения двух сходящихся последовательностей? Приведите пример расходящихся последовательностей, произведение которых сходится.
Произведения
двух сходящихся последовательностей
и
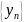 есть сходящаяся последовательность,
предел которой равен произведению
пределов соответствующих последовательностей.
Пусть
есть сходящаяся последовательность,
предел которой равен произведению
пределов соответствующих последовательностей.
Пусть
 – две сходящиеся последовательности,
причем
– две сходящиеся последовательности,
причем
,
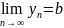 ,
тогда
,
тогда
 .
.
Пример расходящихся последовательностей, произведение которых сходится
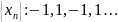
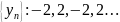
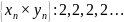
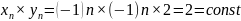

Дайте определение бесконечно малой последовательности. Приведите примеры бесконечно малых последовательностей, отношение которых: а) является бесконечно малой последовательностью; б) не является бесконечно малой последовательностью.
Последовательность
называется бесконечно малой, если
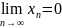 .
.
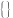 и
– бесконечно малые последовательности,
т.к.
и
– бесконечно малые последовательности,
т.к.
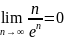
и
– бесконечно малые последовательности,
т.к.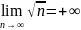
Докажите, что произведение бесконечно малой и ограниченной последовательностей является бесконечно малой последовательностью.
Произведение
бесконечно малой на ограниченную
последовательность есть бесконечно
малая. Доказательство:
Пусть
– ограниченная, а
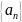 - бесконечно малая последовательность.
В силу ограниченности последовательности
существует такое число А, что любой
элемент ее удовлетворяет неравенству
- бесконечно малая последовательность.
В силу ограниченности последовательности
существует такое число А, что любой
элемент ее удовлетворяет неравенству
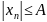 .
Поскольку последовательность
бесконечно малая, для положительного
числа
.
Поскольку последовательность
бесконечно малая, для положительного
числа
 существует такой номер N,
что при всех
существует такой номер N,
что при всех
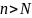
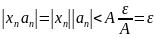 .
Т.о.
.
Т.о.
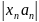 – бесконечно малая.
– бесконечно малая.
Дайте определение бесконечно большой последовательности. Что означает запись: “
 ”?
”?
Последовательность
называется бесконечно большой, если
для любого положительного числа А
существует такой номер N, что при
(для всех элементов последовательности)
выполняется неравенство.
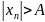 .
.
означает, что для любого A>0, сущ. N, для любого n ≥ N: |Xn| > A.
Всякая ли неограниченная последовательность является бесконечно большой? Ответ обоснуйте.
Всякая бесконечно большая последовательность является неограниченной, однако неограниченная не обязательно является бесконечно большой. Рассмотрим следующий пример: неограниченная послед-ь 1, 2, 1, 3 .., 1, n, 1, n + 1 … не является бб, поскольку при А > 1 неравенство |Xn| > A не имеет места для всех элементов Xn с нечетными номерами.
Приведите пример двух бесконечно больших последовательностей, сумма которых является бесконечно малой последовательностью.
Две
бесконечно большие последовательности,
суммы которых являются бесконечно
малой последовательностью. Сумма
убывающей и ограниченной последовательности
(1, 1/3, 1/5,…, 1/(2n-1)…) и возрастающей
неограниченной последовательности
(1,2,3,4,…n) является бесконечно малой
последовательностью. Или пример:

Дайте определение возрастающей последовательности. Что можно сказать о пределе возрастающей последовательности, если она: а) ограничена сверху; б) не ограничена? Ответ обоснуйте.
Последовательность {Xn}называется возрастающей, если xn < xn+1 для всех n.
Любая монотонная ограниченная последовательность имеет предел. Геометрически это означает, что если последовательность {Xn} возрастает, и при этом ограничена сверху, то это означает, что с ростом n точки хn на числовой оси смещаются вправо, но при этом не переходят через некоторый рубеж А. Геометрически ясно, что в этом случае числа xn должны накапливаться к некоторому числу а, которое и будет пределом последовательности {Xn}. Следовательно, в случае б) предела у данной последовательности просто не существует.
В случае а) предел данной последовательности меньше или равен граничному члену данной последовательности.
2.Предел функции
Дайте определение предела функции в точке. Найдите, исходя из определения,
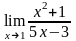 .
.
Определение:
число А называется пределом функции
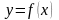 в точке x0,
если для любой сходящейся к x0
последовательности
значений аргумента x
(отличных от х0)
соответствующая последовательность
значений функции сходится к числу А.
в точке x0,
если для любой сходящейся к x0
последовательности
значений аргумента x
(отличных от х0)
соответствующая последовательность
значений функции сходится к числу А.
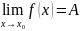
=
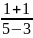 =
=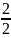 = 1
= 1
На рисунке изображен график функции .

Существуют
ли следующие пределы а)
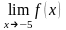 ;
б)
;
б)
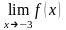 ;
в)
;
в)
 ?
Дайте обоснованные ответы и найдите
пределы (если они существуют).
?
Дайте обоснованные ответы и найдите
пределы (если они существуют).
а) - существует, равен 3; б) - не существует, точка разрыва 2 рода: правост и левост пределы равны +бесконечности; в) предел существует, функция сходится к данной точке, предел равен 1
Докажите, что предел суммы двух функций равен сумме их пределов, если последние существуют.
Предел
суммы двух функций равен сумме их
пределов
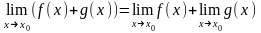
В
силу Теоремы 1 О пределах функции (
функция f(x)
может иметь в точке х0
только один предел)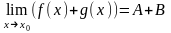 где
где
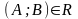 ,
тогда
,
тогда
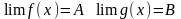 ;
т.о
;
т.о
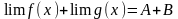
Докажите, что функция
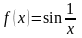 не имеет предела в точке
не имеет предела в точке
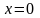 .
.
Предела
функции
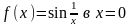 не
существует т.к если рассматривать
предел, то в нем 1/0 = ∞. А сам график
синуса ограничен на отрезке [-1;1]. Таким
образом, если рассматривать график
синуса, то при стремлении его к
бесконечности, значение функции может
быть любым в промежутке от -1 до 1. Т.е.
значение неопределенно.
не
существует т.к если рассматривать
предел, то в нем 1/0 = ∞. А сам график
синуса ограничен на отрезке [-1;1]. Таким
образом, если рассматривать график
синуса, то при стремлении его к
бесконечности, значение функции может
быть любым в промежутке от -1 до 1. Т.е.
значение неопределенно.
Дайте определение предела функции при
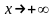 .
Докажите, что функция
.
Докажите, что функция
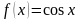 не имеет предела при
.
не имеет предела при
.
Пределом функции f(x) при x→+∞ называют число а, если для любой послед-и {Xn} значений аргумента, послед-ь {f(Xn)} значений функции сходится к пределу а: lim (x→∞) f(x) = a. f(x) = cosx => limx→+∞cosx=(-1;+1), что невозможно. Вообще значения функции косинус – ограниченная последовательность, не сходящаяся.
Дайте определения односторонних пределов функции в точке. Что можно сказать об односторонних пределах функции
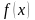 в точке
в точке
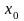 ,
если
,
если
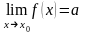 ?
Ответ обоснуйте.
?
Ответ обоснуйте.
lim (x→a+0) f(x) = b; lim (x→a-0) f(x) = c
Число b называется правым пределом f(x) в точке А, если для любой послед-и значений аргумента Xn, сходящихся к А и состоящих из чисел больше А (справа), соответствующая послед-ь значений функции сходится к числу b. Число с называется левым пределом f(x) в точке А, если для любой послед-и значений аргумента Xn, сходящихся к А и состоящих из чисел меньше А (слева), соответствующая послед-ь значений функции сходится к числу с.
В случае Lim (x→ х0) f(x)=a односторонние пределы тоже устремлены к a. Обоснованием является существование данного предела в точке. Теорема: Функция f(x) имеет предел в точке x0 тогда и только тогда, когда в этой точке сущ. пределы слева и справа (они должны быть равны).
