50.Сформулируйте признак Даламбера в предельной форме. Приведите пример сходящегося ряда с положительными членами, к которому этот признак неприменим.

Если существует предел: , то

1. при L < 1 ряд сходится

2. при L > 1 ряд расходится

3. при L = 1 необходимы доп. исследования. (признак неприменим)

Пример:

Докажем сходимость: сравним с рядом: . Поскольку при всех n => достаточно доказать сходимость этого ряда. Так как , то = Т.о. . Этот ряд сходится => искомый ряд тоже сходится. Признак Даламбера не работает:

59. Сформулируйте теорему о почленном дифференцировании степенного ряда. Используя эту теорему, найдите разложение функции в ряд Маклорена, исходя из разложения функции . Теорема о почленном дифференцировании степенного ряда: пусть функция f(x) разлагается на интервале (-R,R) в степенной ряд: f(x) = a₀+a₁x+a₂x²+…+a_nxⁿ+…(1). Рассмотрим степенной ряд: a₁+2a₂x+…+na_nx^n-1+…(2), полученный почленным дифференцированием ряда (1). Тогда:

1. ряд (2) имеет тот же радиус сходимости R, что и ряд (1).

2. на всем интервале (-R,R) функция f(x) имеет производную f^,(x), которая разлагается в степенной ряд (2)

ряд для cosx получается почленным дифференцированием ряда Sinx=x-(x³/3!)+(x⁵/5!)-…+(-1)ⁿ(x²ⁿ⁺¹/(2n+1)!)+…

(Sinx)’=x’-(x³/3!)’+(x⁵/5!)’-…+((-1)ⁿ(x²ⁿ⁺¹/(2n+1)!))’+…

Cosx=1-x²/2!+x⁴/4!-…+(-1)ⁿ(x²ⁿ/(2n!)

65. Найти значение а, при котором функция является решением дифференциального уравнения - опечатка

69. Дайте определение и приведите пример дифференциального уравнения с разделяющимися переменными. Приведите уравнение к виду уравнения с разделенными переменными. Одним из наиболее простых, но весьма важных типов дифференциальных уравнений являются уравнения с разделяющимися переменными. Это дифференциальные уравнения вида: y’=f(x)g(y), где f(x) и g(y) – непрерывные функции.

Проверим на однородность функцию:

=> однородны.

Уравнение с разделяющимися переменными.

70. Дайте определение и приведите пример автономного дифференциального уравнения. Сформулируйте свойство решений автономного уравнения. Одним из важных частных случаев дифференциальных уравнений с разделяющимися переменными являются так называемые автономные уравнения. Это уравнения вида :y’=g(y).

Замечание: Если у*- корень уравнения g(y)=0, то у=у* (у-const) является решением уравнения y’=g(y). Такое решение называется стационарным.

Теорема: Если у=фи(х) – решение автономного дифференциального уравнения, то у=фи(х+С) также является решением этого уравнения.

Пример: y’=cos(2y+2x+6). Делая замену z=2y+2x+6, находим z’=2y’+2. Следовательно, z’=2cosz+2, или z’=4cos²z/2. 71. Дайте определение уравнения Бернулли. Приведите пример.

Дифференциальное уравнение вида y’+p(x)y=f(x)yⁿ (n≠0, n≠1) называется уравнением Бернулли. Пример: y’-y=e^6x/y². Решение: n=-2. Выполним замену z=y³, получим z’=3y²y’. Далее решаем полученное уравнение: z’-3z=3e^6x

74. Установить линейную зависимость системы функций , , . Пусть функции линейно независимы , тогда составим определитель Вронского:

W(y₁, y₂,…,y_k)=|y₁ y₂ …. Y_k|

| 2 х-1 х+1|

|y’₁y’₂ …. Y’_k| =

| 0 1 1 | = | . …………… | =0 |0 0 0 |

|y₁^(k-1)y₂^(k-1) …. Y_k^(k-1)|

значит функции лин зависимы чтд

Данные функции линейно зависимы так первую функцию можно представить в виде линейной комбинации двух других 2= 1*(x+1)+(-1)+(x-1), соответственно можно подобрать такие α1,α2,α3 при которых верно равенство: α1*y1+α2*y2+α3*y3=0

1*(x+1)+(-1)*(x-1)+(-1)*2=0

67. Сформулируйте теорему существования и единственности решения задачи Коши для дифференциального уравнения первого порядка Проверьте выполнение условий этой теоремы для задачи , Если в некоторой окрестности точки (х₀;у₀) функция f(x,y) определенная, непрерывна и имеет непрерывную частную производную f’_y, то существует такая окрестность точки (х₀;у₀), в которой задача Коши y’=f(x,y), y(x₀)=y₀имеет решение, притом единственное.

Подставим в исходное:

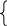
Запишем общее решение:

Подставим значения условий для задачи Коши

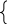
Ответ: с=3 и у=-3х.

6 8. Какое решение дифференциального уравнения называется особым? Найдите особое решение уравнения . Особое решение дифференциального уравнения – это некоторая интегральная прямая уравнения, состоящая из особых точек.

Практика:

Решение уравнения, но есть особые решения при y(x)=0.

75. Докажите, что сумма частного решения линейного неоднородного дифференциального уравнения второго порядка и общего решения соответствующего однородного уравнения является общим решением линейного неоднородного уравнения второго порядка. Общее решение неоднородного уравнения L(y)=f(x)есть сумма частного решения ‾у(х) этого уравнения и общего решения соответствующего ему однородного уравнения L(y)=0. Доказательство: Покажем сначала, что сумма у(х) частного решения уравнения неоднородного уравнения ‾у(х)и произвольного решения у₀(х) однородного уравнения также является решением неоднородного уравнения. Действительно, в силу леммы имеем L(‾y+y₀)=L(‾y)+L(y₀)=f(x)+0=f(x), что и требовалось доказать. Теперь нам осталось доказать, что всякое решение у(х) неоднородного уравнения есть сумма ‾у(х) и некоторого частного решения у₀(х) уравнения L(y)=f(x). Имеем L(у-‾y)=L(y)-L(‾y)=f(x)-f(x)=0.Следовательно, у₀(х)=у(х)-‾у(х) – решение уравнения L(y)=0, значит, у(х)=у₀(х)+‾у(х), что и завершает доказательство.

Возьмем ур-е (1): . Решением ур-я(1) будет сумма частного и общего решения однородного ур-я .

Док-во. Тогда имеем *: . Возьмем любое решение ур-я (1)**:

Вычтем их ** уравнение *, получим: ЧТД

77. Докажите, что общим решением линейного однородного дифференциального уравнения второго порядка является линейная комбинация фундаментальной системы решений этого уравнения. Пусть у₁(х),……, у_п(х) – фундаментальный набор решений уравнения L(y)=0, тогда общее решение этого уравнения задается формулой: y=C₁y₁+…+C_ny_n. Доказательство. То, что функция у(х), определяемая формулой

С₁у₁(х₀)+С₂у₂(х₀)+….+С_ку_к(х₀)=0

С₁у’₁(х₀)+С₂у’₂(х₀)+…+ С_kу’_k(х₀)=0

………………………………………………

С₁у₁^(k-1)(х₀)+С₂у₂^(k-1)(х₀)+…..+ С_kу_k^(k-1)(х₀)=-0

Является решением уравнения L(y)=0, следует из С₁у₁(х)+С₂у₂(х)+….+С_ку_к(х). Покажем теперь что любое решение ѱ (х) уравнения L(y)=0 представимо в виде линейной комбинации функций у₁,…,у_п. Зафиксируем некоторую точку х₀. Введем следующие обозначения ѱ(х₀)=у₀, ѱ’(x₀)=y’₀, …., ѱ^(n-1)(x₀)=y₀^(n-1) рассмотрим систему линейных алгебраических уравнений:

С₁у₁(х₀)+С₂у₂(х₀)+….+С_nу_n(х₀)=y₀

С₁у’₁(х₀)+С₂у’₂(х₀)+…+ С_nу’_n(х₀)=y₀

………………………………………………

С₁у₁^(n-1)(х₀)+С₂у₂^(n-1)(х₀)+…..+ С_nу_n^(n-1)(х₀)=y₀^(n-1)

Определителем этой системы является определитель Вронского для функции у₁,…у_п в точке х₀. Ввиду линейной зависимости этих функций данный определитель не равен нулю. Следовательно, у системы

С₁у₁(х₀)+С₂у₂(х₀)+….+С_nу_n(х₀)=y₀(1.1)

С₁у’₁(х₀)+С₂у’₂(х₀)+…+ С_nу’_n(х₀)=y₀

………………………………………………

С₁у₁^(n-1)(х₀)+С₂у₂^(n-1)(х₀)+…..+ С_nу_n^(n-1)(х₀)=y₀^(n-1)

Существует решение (‾С₁, ‾С₂,….,‾С_п). Тогда функция у(х)=‾С₁у₁(х)+‾С₂у₂(х)+…+‾С_пу_п(х), как это вытекает из (1.1), удовлетворяет тем же начальным условиям. В силу единственности решения задачи Коши имеем ѱ(х)=у(х), т.е. ѱ(х) есть линейная комбинация функции у₁,…у_п. теорема доказана.