1. Докажите, что если и – первообразные функции на интервале Х, то , где С – некоторая постоянная. Если F(x)- первообразная для функции у=f(x) на промежутке Х, то все первообразные для функции y=f(x) имеют вид F(x)+C, где С – произвольная постоянная. Доказательство: Пусть F(x) – первообразная для f(x)тогда выполняется равенствоF’(x)=f(x). Для любой постоянной С. (F(x)+C)’=F’(x)+0=f(x), а это означает, что F(x)+C–также первообразная для f(x). Обратно, пусть на ряду с данной первообразной F(x) функция F₁(x) – также первообразная для f(x). Тогда выполняются равенстваF₁’(x)=F’(x)=f(x), откуда (F₁ (x)-F(x))’=0тогда по теореме о непрерывности функции разность этих двух первообразных будет тождественно равна константе F₁(x)-F(x)=C, илиF₁(x)=F(x)+C, что завершает доказательство теоремы.

2. Докажите, что . (⌠f(x)dx)’=f(x), d(⌠f(x)dx)=f(x)dx

Док-во: (⌠f(x)dx)’=(F(x)+C)’=f(x); d(⌠f(x)dx)=(⌠f(x)dx)’)=f(x)dx

3. Докажите формулу интегрирования по частям для неопределенного интеграла. Пусть u(x) и v(x)-две дифференцируемые функции на промежутке X. Тогда на X выполняется формула интегрирования по частям: ⌠udv=uv-⌠vdu

Док-во: имеем формулу для дифференциала произведений функции uv: d(uv)=udv+vdu. Проинтегрируем обе части и получим ⌠d(uv)=⌠udv+⌠vdu; uv=⌠udv+⌠vdu. Откуда легко получается формула ⌠udv=uv-⌠vdu

4. Докажите формулу замены переменной для неопределенного интеграла. Пусть функция x=ѱ(t) определена и дифференцируема на промежутке T иX-множество ее значений, на котором определена функция f(x). Тогда если F(x)-первообразная для f(x) на X, то F(ѱ(t))-первообразная для f(ѱ(t)) ѱ’(t)dtна T, т.е. на множестве T выполняется равенство: ⌠f(x)dx│_x=ѱ(t)=⌠f(ѱ(t)) ѱ’(t)dt

Док-во:по правилу дифференцирования сложной функции производная левой части: F’_t(ѱ(t))=F’_x(ѱ(t))*ѱ’(t)=f(ѱ(t))*ѱ’(t) что совпадает с подинтегральной функцией в пр. части равенства

5. Докажите, что если функция f(t) непрерывна на отрезке [a,b], то функция F(x)= дифференцируема на (a,b) и F’(x)=f(x). Доказательство:

По теореме о среднем найдется точка с такая ,что . Так как f(x) непрерывна и с

Поэтому

6. Используя свойство интеграла с переменным верхним пределом, докажите формулу Ньютона-Лейбница. Пусть функция y=f(x) непрерывна на отрезке [a,b] и F(x)-первообразная для f(x). Тогда ⌠^b_af(x)dx=F(b)-F(a)

Док-во:Т.кf(x)-непрерывна на [a,b], то она интегрируема на [a,b] и имеет на нем первообразную Ф(х)=⌠^x_af(t)dt, подставляя х=b, получим Ф(b)=⌠^b_af(t)dt, а подставляя x=a, Ф(а)=⌠^а_af(t)dt=0, поэтому ⌠^b_af(x)dx=Ф(b)-Ф(a), если F(x)-другая первообр для f(x), то выполняется равенство F(x)=Ф(x)+C. имеем F(b)-F(a)=(Ф(b)+C)- (Ф(a)+C)= Ф(b)-Ф(a)=⌠^b_af(x)dx

9. Сходится ли интеграл ? Ответ обоснуйте

В силу того, что ¼ является const, а sin4x-ограничено, то предел ограничен тоже, значит он сходится, а значит сходится и сам интеграл.

7. Применив замену переменной в определенном интеграле, докажите, что для любой четной непрерывной на отрезке функции справедливо равенство . В чем состоит его геометрический смысл?

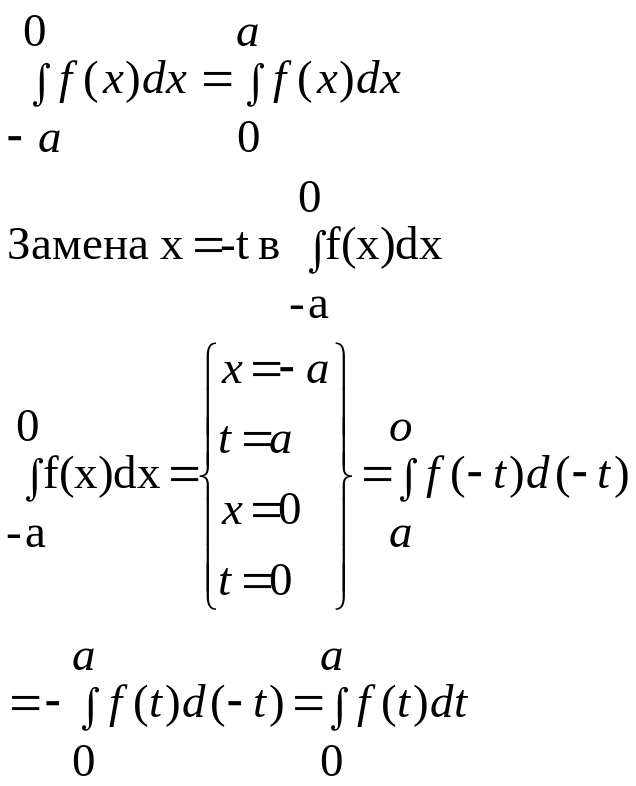
-a

a

8. Применив замену переменной в определенном интеграле, докажите, что для любой нечетной непрерывной на отрезке функции f(x) справедливо равенство . В чем состоит его геометрический смысл? Так как f(x) непрерывна на [-a,a], тогда пусть х=g(t) определена на [ ] и имеет производную внутри этого отрезка, причем g(

Доказательство

Пусть F(x) – первообразная f(x), тогда F’(x)=f(x) F(g(t))’=F’(g(t))*g’(t)

Пусть и g(

Можно заметить, что если подынтегральная функция f(x) нечетная на отрезке [a,b], то F(x) четная на этом отрезке, т.е. F(-x)=F(x)

1)рассмотрим =

=F(0)-F(a)

2) рассмотрим ==-(F(0)-F(а)) , ч.т. д

Геометрический смысл. Определенный интеграл равен площади криволинейной трапеции, ограниченной вертикальными прямыми х=а, x=b при a<b, осью Ох и графиком неотрицательной и непрерывной функции y=f(x)

10. Сходится ли интеграл ? Ответ обоснуйте.

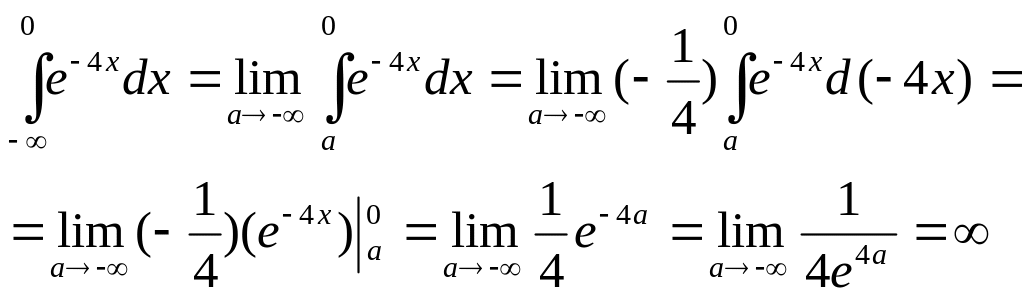
интеграл расходится в силу расходимости предела.

14. Дайте определение расстояния между точками . Сформулируйте и докажите свойства функции .

В R¹:расстояние между точками x₁иx₂ равно │x₁ –x₂│

R²:P(x₁,y₁) иQ(x₂,y₂), то ρ(P,Q)=√( y₁ - x₁)²+( y₂ –x₂)²)

R³: P(x₁,y₁,z₁) иQ(x₂,y₂,z₂), тоρ(P,Q)=√( x₁ – x₂)²+( y₁ – y₂)² +(( z₁ – z₂)²)

Rⁿ: ρ(p,q)=│p-q│=√( x’₁ – x’’₁)²+…+( x’_n– x’’_n)²)

В , где n>3, расстояние между точками определяется формулой

Где, А и В – две произвольные точки из .

Свойства:

1. Ρ(p,q)>0, если p≠qи ρ(p,p)=0 доказательство: P=√(x₁-x₂)²+(y₁-y₂)² >0, P=0, если x₂=x₁, y₂=y₁. т.е. p=q

2. Ρ(p,q)=Ρ(q,p) доказательство: P(p;q)=√( x₁-x₂)²+(y₁-y₂)²=√(x₂-x₁)²+(y₂-y₁)²=P(q;p)

Доказательства: Первые два свойства очевидным образом следуют из определения расстояния.

1)Область значений функции равна .

2) Дано: , тогда ; .

3. Ρ(p,q)+Ρ(q,r)≥ Ρ(p,r)

Док-во:ρ(p,q)+ρ(q,r)≥ρ(p,r). Проверим сначала такое равенство: √∑(a_i+b_i)²≤√∑a_i²+√∑b_i², где а₁…a_n,b₁….b_n- какие угодно числа

Взяв любое число х, запишем: ∑(a_iх+b)²=x²∑a_i²+2x∑a_ib_i+∑b_i²=αx²+2βx+γ, где α,β,γ- обозначают соответственно ∑a_i²,∑a_ib_i , ∑b_i². Очевидно α≥0 γ≥0. Квадратный трехчлен αx²+2βx+γ как показывает левая часть равенства неотрицателен при любом значении х. следовательно его дискриминант β²-αγ≤0, откуда имеем β²≤αγ или ∑a_ib_i≤∑a_i²*∑b_i². Но если возвести в квадрат обе части √∑(a_i+b_i)²≤√∑a_i²+√∑b_i²и сократить справа разные слагаемые, то получим ∑a_ib_i≤∑a_i²*∑b_i². Опираясь на √∑(a_i+b_i)²≤√∑a_i²+√∑b_i² докажем неравенство треугольника. Если a_i=х_i-y_i;b_i= z_i -y_i , так что a_i+ b_i= z_i- x_i , то придем к √∑(y_i-x_i)²+√∑(z_i-y_i)²≥√∑(z_i-x_i)²т.е. к неравенству треугольника для трех точек p,q,r.

15. Дайте определение открытого множества в . Является ли множество открытым? Множество D называется открытым, если все его точки внутренние (замкнутым, если оно содержит все свои граничные точки). Множество не является открытым, т.к. точка , принадлежит D, но в любой её сколько угодно малой окрестности есть точки, не лежащие в D (например, точки (х,у), для которых .

16. Дайте определение замкнутого множества в . Является ли множество замкнутым? Множество {M} называется замкнутым, если все граничащие точки принадлежат этому множеству.

Множество Х называется замкнутым, если оно содержит все свои граничные точки. Точка р называется граничной точкой для Х, если любая её окрестность содержит как точки, принадлежащие Х, так и точки, не принадлежащие Х.

Множество не является закрытым, т.к. точка , не принадлежит D, но в любой её окрестности есть точки, лежащие в D.

17. Дайте определение открытого множества в . Является ли множество открытым? Множество D называется открытым, если все его точки внутренние (замкнутым, если оно содержит все свои граничные точки).

Множество Х называется открытым, если все его точки внутренние. Точка р называется внутренней точкой множества Х , если она содержится в Х вместе с некоторой своей .

Множество является открытым, т.к. точки лежит в D.

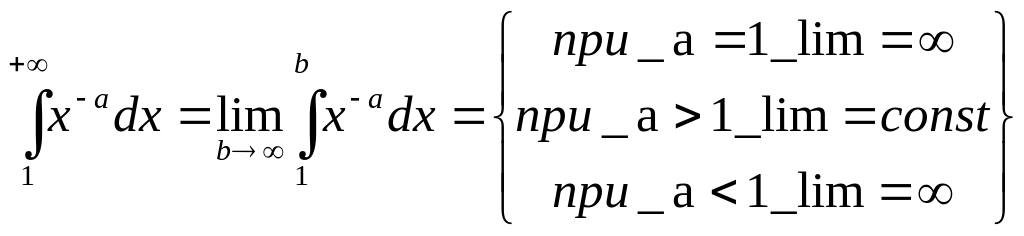_{11. При каких значениях сходится интеграл ?} при а>1 предел равен const и интеграл сходится в силу сходимости предела, получается, что ответ: при a>1.

18. Дайте определение предельной точки множества. Приведите примеры: а) множества, содержащего все свои предельные точки, б) множества, для которого существует предельная точка, ему не принадлежащая. Точка М₀ называется предельной точкой множества {M}, если в любой ее окрестности существуют точки множества {M}, отличные от М₀

Послед-ть {1/n}_n=1^∞имеет единственную предельную точку ноль, ей не принадлежащую

Пусть Х – множество в , точка называется предельной для Х, если в любой Х, отличные от .

А) замкнутый круг:

Б) замкнутый круг без своего центра . В этом случае центр (0,0) и есть та предельная точка, которая не принадлежит самому множеству.

19. Дайте определение сходящейся последовательности точек в . К какой точке в сходится последовательность ? Пусть {p_n}- последовательность точек в Rⁿ. Мы говорим, что эта последовательность сходится к точке p_o, если числовая последовательность {ρ(p_n,p₀)} имеет предел 0.

Пусть p₁=(x₁,y₁), p₂=(x₂,y₂),…-последовательность точек в R². Мы скажем, что эта последовательность сходится к точке p0=(x₀,y₀), если числовая последовательность x₁,x₂,… сходится к числу x₀, а числовая последовательность y₁,y₂,…- к числу y₀.

Пусть - последовательность точек в . Мы говорим, что эта последовательность сходится к точке , если числовая последовательность имеет предел 0. Если А – предел последовательности, то говорят, что сходится к точки А.

Поскольку то А=(

20. Дайте определение сходящейся последовательности точек в . К какой точке в сходится последовательность ? Пусть {p_n}- последовательность точек в Rⁿ. Мы говорим, что эта последовательность сходится к точке p_o, если числовая последовательность {ρ(p_n,p₀)} имеет предел 0.

Пусть p₁=(x₁,y₁), p₂=(x₂,y₂),…-последовательность точек в R². Мы скажем, что эта последовательность сходится к точке p0=(x₀,y₀), если числовая последовательность x₁,x₂,… сходится к числу x₀, а числовая последовательность y₁,y₂,…- к числу y₀.

Пусть - последовательность точек в . Мы говорим, что эта последовательность сходится к точке , если числовая последовательность имеет придел 0. Если А – предел последовательности, то говорят, что сходится к точки А.

Поскольку = , то А=(

22. Дайте определение предела функции двух переменных в точке. Докажите, что функция не имеет предела в точке . Пусть на множестве Х-Rⁿ задана функция f(p) и пусть p₀- предельная точка для Х. Число а называется пределом функции f в точке p₀, если для любой сходящейся к p₀ последовательности {p_n}, где все p_n≠p₀, соответствующая числовая последовательность {f(p_n)} сходится к числу а. Запись: limf(p)=a при p к p_{0 =>}

Рассмотрим две последовательности точек, сходящихся к (0,0) :

(0; ) и ( ;0)

1. = =-1 и -1

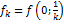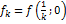2. = =-1 и

26. Дайте определение частных производных функции в точке . Найдите, исходя из определения, частные производные функции в точке . Частной производной функции нескольких переменных по одной из этих переменных называется предел отношения частного приращения функции к приращению соответствующей независимой переменной, когда это приращение стремится к нулю.

Z’_x=lim∆_xZ/∆x=lim(f(x₀+∆x,y₀)-f(x₀,y₀))/∆x при ∆х к нулю

Z’_y=lim∆_yZ/∆y=lim(f(x₀,y₀+∆y)-f(x₀,y₀))/∆y при ∆y к нулю

Найти частные производные

=y*2x=4

= =1

27. Дайте определение дифференцируемости функции в точке . Докажите, что если функция дифференцируема в точке , то она непрерывна в этой точке. Функцияz=f(x,y) называется дифференцируемой в точке (x₀,y₀), если ее полное приращение можно представить в виде: ∆z=f(x,y)-f(x₀,y₀)=f’_x(x₀,y₀)∆x+ f’_y(x₀,y₀)∆y+eρ, либо∆z=dz+ eρ, гдее=е(∆x,∆y)- функция бесконечно малая при ∆x→0,∆y→0; ρ=√((∆x)²+∆y²)-расстояниеотточки (x,y) до точки (x₀,y₀)

Если функция z=f(x,y) дифференцируема в точке (x₀,y₀), то она непрерывна в этой точке.

Док-во: необходимо проверить, что ∆z→0, когда ∆х→0, ∆y→0. Вычислим:

lim∆z=lim(dz+eρ)=z’_x*lim∆x+z’_y*lim∆y+lime*limρ=z’_x*0+z’_y*0+0*0=0 (подвсемиlim∆х→0, ∆y→0)

28. Дайте определение дифференциала функции в точке . Какая функция называется дифференцируемой в точке ? Полный дифференциал функции выполняет роль линейного приближения и определяется как сумма произведений частных производных функции на приращения независимых переменных: dz=z’x∆x+z’y∆y. Функцияz=f(x,y) называетсядифференцируемойвточке (x₀,y₀), еслиееполноеприращениеможнопредставитьввиде: ∆z=f(x,y)-f(x₀,y₀)=f’_x(x₀,y₀)∆x+ f’_y(x₀,y₀)∆y+eρ, либо ∆z=dz+ eρ, гдее=е(∆x,∆y)- функциябесконечномалаяпри ∆x→0,∆y→0; ρ=√((∆x)²+∆y²)-расстояние от точки (x,y) доточки (x₀,y₀). Пример: z=xy

29. Как связаны производная по направлению и градиент дифференцируемой функции ? Чему равна производная по направлению, перпендикулярному градиенту? Связь градиента и производной по направлению

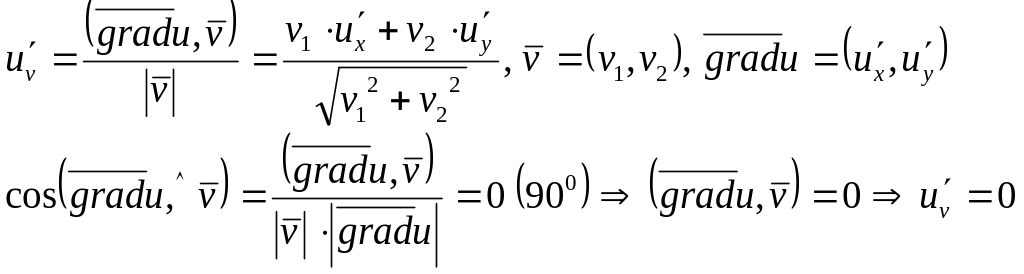
30. Дайте определение градиента функции в точке . Докажите, что в направлении градиента происходит наиболее быстрый рост функции. Чему равна скорость этого роста? Градиентом ф-ции z= f(x,y) в точке M(x,y) называется вектор, координаты которого равны соответствующим частным производным , взятым в точке M(x,y).Gradf(M)=(f’x(M),f’y(M)).

Пусть M(x₀,y₀) точка в которой вычисляется градиент функции f(x,y),ѱ- угол между Gradf(M) и е↑. Так как (Gradf(M), е↑)= |Gradf(M)| *│е↑│*cosѱ, а е↑-единичный вектор, то из формулы вытекает равенство δf(M)/δe=│Gradf(M)│*cosѱ, отсюда следует, что производная в направлении е↑ принимает наибольшее значение при cosѱ=1, те когда направление градиента совпадает с е↑. при этом │Gradf(M)│=δf(M)/δe

Градиент указывает направление наискорейшего роста функции, а максимальная скорость роста равна модулю градиента.

31. Дайте определение однородной функции степени . Является ли функция однородной? Функция z(x;y) называется однородной степени α, если для любой точки (х;у) из области определения и переменной t выполняется равенство z(tx;ty)= t^α z(x;y). Да, является. 2 степени. =t²

32. Дайте определение однородной функции нескольких переменных. Приведите пример однородной функции степени 3, не являющейся рациональной функцией. Пусть D из Rⁿ – область в Rⁿ, содержащая с каждой своей точкой (x1, x2, …., xn) и все точки вида (tx1, tx2, …., txn) при t>0. Функция f(x1, x2, …., xn) с такой областью определения D называется однородной степени λ, если для любого t>0 выполнятся равенство f (tx1, tx2, …., txn)=tλ f(x1, x2, …., xn). Пример однородной функции степени 3:

F (x,y)=x²

F (tx, ty)=t²x²√(tx*ty)=t³ F (x,y)

34. Дайте определение локального экстремума функции двух переменных. Является ли равенство нулю частных производных функции в некоторой точке достаточным условием ее локального экстремума в этой точке? Точка а↑ называется точкой локального максимума (мин) функции f(x↑), если существует такая е-окрестность U_e(a↑)={x↑ϵRⁿ:│x↑-a↑│<e}точки а↑, в которой для любой точки х↑ϵU_e(a↑) выполняется равенство f(x↑)≤f(a↑) (f(x↑)≥f(a↑)). Точки локального максимума и локального минимума называются точками локального экстремума или просто точками экстремума.

Нет, так как достаточным условием: Пусть функция nпеременных f(x↑) имеет в окрестности своей стационарной точки а↑ непрерывные частные производные второго порядка, тогда: если квадр форма d²f_a↑пол определена, то а↑- точка лок мин f (для пол наоборот).

Пусть функция f(x,y) имеет непрчастнпроизв второго порядка в некоторой окрестности своей стационарной точки P. Положим ∆=detf’’(P)=f’’_xx(P) f’’_yy(P)-( f’’_xy(P))²тогда если ∆>0, то в точке Р функция имеет лок экстремум, при чем f’’_xx(P)<0-лок макс, f’’_xx(P)>0- лок мин; если ∆<0, то в точке Р нет экстремума

35. Дайте определение локального экстремума функции двух переменных. Имеет ли функция локальный экстремум в точке ? Точка а↑ называется точкой локального максимума (мин) функции f(x↑), если существует такая е-окрестность U_e(a↑)={x↑ϵRⁿ:│x↑-a↑│<e} точки а↑, в которой для любой точки х↑ϵU_e(a↑) выполняется равенство f(x↑)≤f(a↑) (f(x↑)≥f(a↑)). Точки локального максимума и локального минимума называются точками локального экстремума или просто точками экстремума.

Имеет ли функция f (x,y)=x⁶y⁴ локальным экстремумом в точке (0,0)?

необходим.условие: f ‘x=6x⁵y⁴, f ‘y=4x⁶y³ – выполнено в т.(0,0).2) достаточное усл.: f”xx=30 y⁴x⁴, f”xy=24 x⁵y³, f”yy=12x⁶y². определитель = посчитай сам. опр(0,0)=0=>теорема не дает ответ.

Поэтому: Мо-т.max/min ф-цииf(M) если существ.окрестностьMо такая что для всех М принадлеж. выколот.окрестн.Мо выполняется f(M)>=f(Mo).При y=xf=x⁵ => при x>0 f(x,x) >0 = f(0,0). При x<0 f(x,x)<0=f(0,0). Лок.экстремума нет.

36. Дайте определение локального экстремума функции двух переменных. Имеет ли функция локальный экстремум в точке ? Точка а↑ называется точкой локального максимума (мин) функции f(x↑), если существует такая е-окрестность U_e(a↑)={x↑ϵRⁿ:│x↑-a↑│<e} точки а↑, в которой для любой точки х↑ϵU_e(a↑) выполняется равенство f(x↑)≤f(a↑) (f(x↑)≥f(a↑)). Точки локального максимума и локального минимума называются точками локального экстремума или просто точками экстремума.

Имеет ли функция f (x,y)=xy⁴ локальным экстремумом в точке (0,0)?

необходим.условие: f ‘x=y⁴, f ‘y=4xy³ – выполнено в т.(0,0).2) достаточное усл.: f”xx=0, f”xy=4y³, f”yy=12xy². определитель = -16y⁶. опр(0,0)=0=>теорема не дает ответ.

Поэтому: Мо-т.max/min ф-цииf(M) если существ.окрестностьMо такая что для всех М принадлеж. выколот.окрестн.Мо выполняется f(M)>=f(Mo).При y=xf=x⁵ => при x>0 f(x,x) >0 = f(0,0). При x<0 f(x,x)<0=f(0,0). Лок.экстремума нет.

37. Сформулируйте достаточное условие локального экстремума функции двух переменных. Имеет ли функция в точке локальный экстремум? Пусть функция n переменных f(x↑) имеет в окрестности своей стационарной точки а↑ непрерывные частные производные второго порядка, тогда: если квадр форма d²f_a↑ пол определена, то а↑- точка лок мин f (для пол наоборот ).

Пусть функция f(x,y) имеет непрчастнпроизв второго порядка в некоторой окрестности своей стационарной точки P. Положим ∆=detf’’(P)=f’’_xx(P) f’’_yy(P)-( f’’_xy(P))² тогда если ∆>0, то в точке Р функция имеет лок экстремум, при чем f’’_xx(P)<0-лок макс, f’’_xx(P)>0- лок мин; если ∆<0, то в точке Р нет экстремума

необходим.условие: f ‘x=2x, f ‘y=-2y – выполнено в т.(0,0).2) достаточное усл.: f”xx=2, f”xy=0, f”yy=-2. определитель = -4. Экстремумов нет