44. Дайте определение числового ряда и его суммы. Найдите, исходя из определения, сумму ряда при

Пусть q=1/x, где х>1 и может не являться целым числом, то

, ряд является геометрической прогрессией.

45. Дайте определения числового ряда и его суммы. Исходя из определения докажите, что сумма ряда равна числу 1. пусть дана числовая последовательность а_1, а₂, а₃, …., а_п,…. Выражение вида: а_1, а₂, а₃, …., а_п,….=∑а_п – называют числовым рядом или просто рядом. Сумма числового ряда определяется как предел, к которому стремятся суммы первых n слагаемых ряда, когда n неограниченно растёт. Если такой предел существует и конечен, то говорят, что ряд сходится, в противном случае — что он расходится. Элементы ряда a_n представляют собой либо вещественные, либо комплексные числа.

Практика:

Рассмотрим отдельно дробь :

+1

Возвращаясь к ряду :

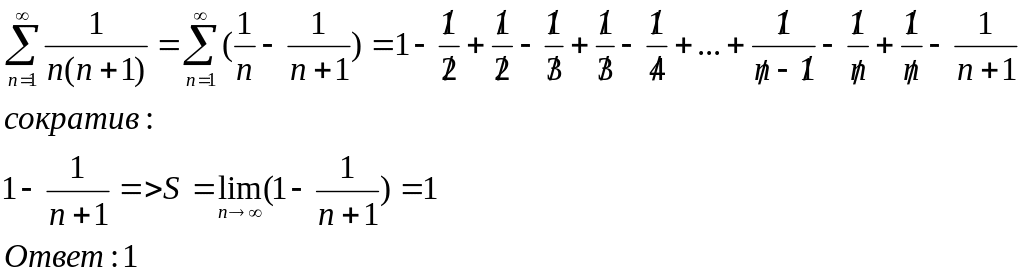
47. Докажите, что если ряд сходится, а ряд расходится, то ряд расходится. Необходимое условие сходимости ряда. Если ряд сходится, то предел его общего члена равен нулю. Док – во. Пусть данный ряд сходится и его сумма равна S. Для любого натурального n имеем S_n=S_n-1+a_n, или a_n=S_n-S_n-1. При n→∞ обе части суммы S_n иS_n-1 стремятся к пределу S_, поэтому из равенства a_n=S_n-S_n-1 следует, что lim_n→∞a_n= lim_n→∞S_n- lim_n→∞S_n-1=S-S=0. Подчеркиваем еще раз, что мы установили, только необходимое условие сходимости ряда, т.е. условие при на рушении которого ряд не сможет сходиться. С помощью этого признака можно доказывать только расходимость ряда.

Докажите, что если ряд сходится, а ряд расходится, то ряд + ) расходится.

Док-во от обратного. Пусть сходится. Тогда = сходится, что противоречит условию.

48. Докажите, что для сходимости ряда , , необходимо и достаточно, чтобы последовательность его частичных сумм была ограничена. Для того чтобы ряд с положительными членами сходился, необходимо и достаточно, чтобы последовательность его частичных сумм была ограничена. Доказательство: необходимость. Пусть a₁+a₂+….+a_n+…. сходится. Тогда существует предел его частичных сумм. Из свойств пределов следует, что последовательность частичных сумм ограничена. Достаточность. Поскольку все члены данного ряда положительны и для любого nS_n=S_n-1+a_n, то последовательность его частичных сумм монотонно возрастает Однако, известно, что ограничения сверху монотонная последовательность имеет предел. Указанный критерий имеет скорее теоретическое, нежели практическое значение. Однако он является основой, на которой базируются другие признаки сходимости. Все они являются только достаточными.

49. Признак Даламбера: Если для ряда с положительными членами a₁+a₂+….+a_n+…. Существует такое число q<1, что при всех n(или, начиная с некоторого n )выполняется неравенство a_n+1/a_n<q, то ряд сходится. Если же a_n+1/a_n>1 для всех или начиная с некоторогоn,то ряд расходится. Док-во: Отбросив, если необходимо. Несколько переменных частей ряда, можно считать, что неравенство, a_n+1/a_n<q выполняется для всех n= 1, 2,…. Перепишем это неравенство в виде a_n+1<qa_n, Отсюда имеем а₂<qa₁, a₃<qa₂<q²a₁, a₄<qa₃<q³a₁ и т.д.; вообще, при любом nсправедливо неравенство a_n<q^n-1a₁. Это показывает, что члены ряда a₁+a₂+….+a_n+…. Не превосходят соответствующих членов бесконечной геометрической прогрессии а₁+а₁q+a₁q²+….+a₁q^n-1+…. Поскольку по условию 0<q<1, эта прогрессия сходится. В силу первого признака сравнения сходится и данный ряд. В случае, когда a_n+1/a_n<1, имеет неравенство a_n+1>a_n, т.е. члены ряда образуют неубывающую последовательность, и поэтому не выполняется необходимый признак сходимости ряда, что доказывает теорему полностью. Признак Даламбера часто применяется в следующей предельной форме.

Очевидно, что данный ряд сходится(по интегральн.признаку), однако d=1(признак Даламбера неприменим)

50. Сформулируйте признак Даламбера в предельной форме для числовых рядов с положительными членами. Приведите пример сходящегося ряда с положительными членами, к которому этот признак не применим. Если существует предел limn→∞a_n+1/a_n=d, то ряд сходится в случае d<1 и расходится в случае d>1. Доказательство: Пусть d<1. Возьмем некоторое число qмежду d и 1: d<q<1. Из условия limn→∞a_n+1/a_n=d следует, что начиная с некоторого номера n, будет выполняться неравенство a_n+1/a_n<q. На основе признака Даламбера отсюда следует сходимость ряда. Случай d>1 разбирается аналогично. В формулировке данной теоремы ничего не говорится о случае d=1. При d=1 возможна как сходимость, так и расходимость ряда. Например, гармонический ряд расходится, а ряд 1/2² +1/3³+ ….+ 1/(n+1)²+…. – сходится.

51. Сформулируйте признаки сравнения для числовых рядов с неотрицательными членами. Используя этот признак, докажите, что ряд расходится . Первый признак сравнения: Пусть даны два ряда с положительными членами: a₁+a₂+….+a_n+…. И b₁+b₂+….+b_n+…., причем члены первого ряда не превосходят соответствующих членов второго: a_n<b_n (n= 1, 2,….). Тогда из сходимости второго ряда («большего») следует сходимость первого ряда («меньшего»). Эквивалентно из расходимости меньшего ряда следует расходимость большего ряда.

Второй признак сравнения: Если для рядов a₁+a₂+….+a_n+…. И b₁+b₂+….+b_n+….,с положительными членами существуют отличный от нуля предел отношения limn→∞a_n/b_n=u, то ряды a₁+a₂+….+a_n+…. И b₁+b₂+….+b_n+…. Сходятся или расходятся одновременно.

Практика:

, доказать расходимость ряда:

Используем сравнительный метод:

, где - меньше . Так как расходится и является меньше, то по первому признаку сравнения. Значит

46. Сформулируйте и докажите необходимое условие сходимости числового ряда. Приведите пример расходящегося ряда, для которого это условие выполнено. пусть дана числовая последовательность а_1, а₂, а₃, …., а_п,…. Выражение вида: а_1, а₂, а₃, …., а_п,….=∑а_п – называют числовым рядом или просто рядом. Сумма числового ряда определяется как предел, к которому стремятся суммы первых n слагаемых ряда, когда n неограниченно растёт. Если такой предел существует и конечен, то говорят, что ряд сходится, в противном случае — что он расходится. Элементы ряда a_n представляют собой либо вещественные, либо комплексные числа. (предел = 0)

52. Сформулируйте интегральный признак сходимости числового ряда с положительными членами. При каких положительных значениях ряд сходится, а при каких расходится? Интегральный признак: Пусть неотрицательная функция y=f(x) определена и монотонно убывает для x>1. Тогда для сходимости ряда f(1)+f(2)+…+f(n)+… необходимо и достаточно, чтобы сходился несобственный интеграл ∫₁^∞f(x)dx

Практика:

, при каких α ряд сходится, при каких расходится.

3) Рассмотрим случай при 0<a<1

Имеем . Сравним с , при , так как - гармонический и расходится, то по первому признаку сравнения исходный ряд тоже сходится.

4) рассмотрим случай при :

Имеем

Получается:

, в силу того что q>0

53. Какой числовой ряд называется гармоническим? Докажите, что гармонический ряд расходится. В математике гармонический ряд представляет собой сумму, составленную из бесконечного количества членов, обратных последовательным числам натурального ряда^[1]:

.

Ряд назван гармоническим, так как каждый его член, начиная со второго, является гармоническим средним двух соседних. Доказать, что гармонический ряд расходится. Док-во: предположим противное. Пусть гармонический ряд сходится и существует предел S=limn→∞S_nего конечных сумм. Тогда рассмотрим предел разности его частичных сумм S_2nи S_n: limn→∞(S_2n-S_n)=limn→∞S_2n-limn→∞S_n=S-S=0. С другой стороны, разность S_2n-S_nможно оценить непосредственно: S_2n-S_n = (1+1/2+…+1/n+….+1/(n+1)+….+1/2n)-(1+1/2+…..+1/n)= 1/(n+1)+ 1/(n+2)+….+1/2n. Оценивая слагаемые, входящие в последнюю сумму 1/(n+1)> 1/2n, 1/(n+2)> 1/2n,…,1/(2n-1)>1/2n, получаем, что для любого натурального nимеет место неравенство S_2n-S_n>1/2n+1/2n+….+1/2n=n*1/2n=1/2, что противоречит условию.

54. Сформулируйте признак Лейбница для знакочередующихся числовых рядов. Приведите пример знакочередующегося ряда, сходящегося условно. Признак Лейбница.Если знаки членов ряда чередуются, а абсолютные величины, монотонно убывая, стремятся к нулю, т. е. < и , то ряд сходится, а для его остатков выполняются неравенства: . Пусть - произвольный знакопеременный ряд. Рассмотрим ряд , составленный из абсолютных величин его членов. Если ряд сходится, то сходится и ряд , при этом ряд называется абсолютно сходящимся. Если ряд сходится, а ряд расходится, то ряд называется условно сходящимся.Пример: - знакочередующийся ряд. Убедимся, что модуль общего члена монотонно убывает:

>1 для всех п. Далее, . Таким образом, по признаку Лейбница данный ряд сходится. Продолжим исследование модуля общего члена данного ряда. Сравним его с общим членом гармонического ряда. Имеем . Следовательно, данный ряд, как и гармонический, расходится. Окончательно можно утверждать, что данный ряд сходится условно.

55. Сформулируйте теорему Абеля для степенных рядов. Может ли ряд , расходящийся в точке , сходиться при ? Если степенной ряд a₀+a₁x+a₂x+…+a_nx_n+… сходится при некотором х=х₀, не равном нулю, то он сходится, и притом абсолютно, при всех х, удовлетворяющих условию |х|<|x₀|; Если ряд a₀+a₁x+a₂x+…+a_nx_n+… расходится при некотором х=х₁, то он расходится при всех х, удовлетворяющих условию |х|>|x₁|

_∑∞a_nxⁿ, расходящийся в точке -2 не может сходиться при х=3, т.к. |-2|<|3| следовательно согласно теореме Абеля ряд в точке х = 3 сходится, и притом абсолютно.

56. Сформулируйте теорему о почленном дифференцировании степенного ряда. Используя эту теорему, найдите сумму ряда при . Теорема о почленном дифференцировании степенного ряда: пусть функция f(x) разлагается на интервале (-R,R) в степенной ряд: f(x) = a₀+a₁x+a₂x²+…+a_nxⁿ+…(1). Рассмотрим степенной ряд: a₁+2a₂x+…+na_nx^n-1+…(2), полученный почленным дифференцированием ряда (1). Тогда:

1. ряд (2) имеет тот же радиус сходимости R, что и ряд (1).

2. на всем интервале (-R,R) функция f(x) имеет производную f^,(x), которая разлагается в степенной ряд (2).

∑nxⁿ=x∑nx^n-1=x∑(xⁿ)’=x/(1-x)²

∑xⁿ=x/(1-x) |x|<1 – сходится

∑nx^n-1=(x/1-x)’=(1-x+x)/1/(1-x)²

57. Сформулируйте достаточное условие разложимости функции в ряд Маклорена. Докажите, что функция разлагается в ряд Маклорена на любом интервале . Достаточное условие разложения функции в ряд Маклорена: пусть функция f(x) определена и бесконечно дифференцируема на интервале (-R,R). Если существует такая постоянная: M=const для любого х (-R, R) <M, n=0,1,2,… , то в этом интервале ряд Маклорена сводится к функции f(x). Имеем: (sinx)’=cosx; (sinx)’’=-sinx, (sinx)’’’=-cosx, (sinx)⁽⁴⁾=sinx. Отсюда видно, что последовательность производных функции sinx периодична с периодом 4. При х=0 получаем sin0=0, sin’(0)=1, sin’’(0)=0, sin’’’(0)=-1 В общем случае все производные четного порядка равны 0, а нечетного sin^(2т+1)(0)=(-1)ⁿОтсюда ряд Маклорена для sinx:Sinx=x-(x³/3!)+(x⁵/5!)-…+(1)ⁿ(x²ⁿ⁺¹/(2n+1)!)+…

58. Сформулируйте достаточное условие разложимости функции в ряд Маклорена. Докажите, что функция разлагается в ряд Маклорена на всей числовой оси. Достаточное условие разложения функции в ряд Маклорена: пусть функция f(x) определена и бесконечно дифференцируема на интервале (-R,R). Если существует такая постоянная: M=const для любого х (-R, R) <M, n=0,1,2,… , то в этом интервале ряд Маклорена сводится к функции f(x). Пусть f(x)=e^x. В любом интервале (-r;r) имеем |f⁽ⁿ⁾(x)|= e^x<e^r. В силу признака Даламбера отсюда следует, что функция е^ч равна сумме своего ряда Маклорена при хϵ(-r;r), а значит, и для любого х ввиду произвольности r. Поскольку f⁽ⁿ⁾(0)=e⁰=1 при любом n, получаем разложение e^x=1+x+(x²/2!)+(x³/3!)+…+(xⁿ/n!)+… справедливо для всех х.

59. Сформулируйте теорему о почленном дифференцировании степенного ряда. Используя эту теорему, найдите разложение функции в ряд Маклорена, исходя из разложения функции . Теорема о почленном дифференцировании степенного ряда: пусть функция f(x) разлагается на интервале (-R,R) в степенной ряд: f(x) = a₀+a₁x+a₂x²+…+a_nxⁿ+…(1). Рассмотрим степенной ряд: a₁+2a₂x+…+na_nx^n-1+…(2), полученный почленным дифференцированием ряда (1). Тогда:

1. ряд (2) имеет тот же радиус сходимости R, что и ряд (1).

2. на всем интервале (-R,R) функция f(x) имеет производную f^,(x), которая разлагается в степенной ряд (2)

ряд для cosx получается почленным дифференцированием ряда Sinx=x-(x³/3!)+(x⁵/5!)-…+(-1)ⁿ(x²ⁿ⁺¹/(2n+1)!)+…

(Sinx)’=x’-(x³/3!)’+(x⁵/5!)’-…+((-1)ⁿ(x²ⁿ⁺¹/(2n+1)!))’+…

Cosx=1-x²/2!+x⁴/4!-…+(-1)ⁿ(x²ⁿ/(2n!)