Пункт 3. Факторный анализ (краткая характеристика) §3.1 Сущность модели факторного анализа

Идея так называемого факторного анализа состоит в том, что структура связей между Р анализируемыми признаками Х ,Х ,...,Х может быть объяснена тем, что каждая переменная Х зависит ( линейно или еще как –то иначе ) от

1) меньшего числа Р′ других, непосредственно не измеримых (скрытых, латентных) факторов f ,f ,...,f , (Р′< Р), которые называют общими и которые в большинстве моделей конструируются так, что они оказываются взаимно некоррелируемы

2) некоторой остаточной компоненты U , которая и обуславливает статистический характер связи между Х и f ,f ,...,f .

Конечная цель статистического исследования, проводимого с помощью аппарата факторного анализа состоит в том, чтобы выявить и интерпретировать патентные факторы с одновременным противоречивым стремлением минимизировать их число, а также выявить степень зависимости Х от их специфических остаточных случайных компонент U , J= . В некотором смысле, искомые общие факторы f ,f ,...,f можно интерпретировать, как причины, а наблюдаемые признаки – как следствия.

Иными словами, факторный анализ можно рассматривать как метод сжатия информации, или, что то же, как и метод снижения размерности исходного факторного пространства Х, поскольку корреляция между исследуемыми признаками означает их избыточность, а сведение многих избыточных признаков к немногим вспомогательным(общим факторам), свободным от избыточности, и является задачей сжатия информации (сжатия размерности).

§3.2 Общий вид линейной модели. Ее связь с главными компонентами

Как и ранее компоненты исходных признаков Х ,Х ,...,Х и компоненты исследуемых наблюдений X ,...,X . V= будем полагать центрируемыми, т.е.

Тогда линейная модель факторного анализа примет вид:

или в покомпонентной записи:

здесь

- матрица нагрузок общих факторов на исследуемые признаки.

F = (f , f ,..., f ) - вектор общих факторов

U = (u , u ,..., u ) – вектор случайных компонент остаточных факторов.

Для каждого вектора наблюдения X (v = ) из 3.1 получаем

Д алее предполагают, что U не зависит от F и имеет U~ N(0,V) – р- мерное нормальное распределение, с нулевым вектором средних и диагональной ковариационной матрицей V v = Du (т.е. компоненты u и u , i≠j, i,j = - независимы.)

Вектор общих факторов F может интерпретироваться, в зависимости от содержания конкретной задачи, либо как р’ – мерная нормальная случайная величина со средним MF = 0 и ковариационной матрицей специального вида E(ET )= I , либо как вектор неизвестных неслучайных параметров(вспомогательных переменных), меняющихся от наблюдения к наблюдению.

В обоих случаях интерпретируя F, вектор Х оказался имеющим многомерное нормальное распределение. При этом из сделанных выше допущений имеем :

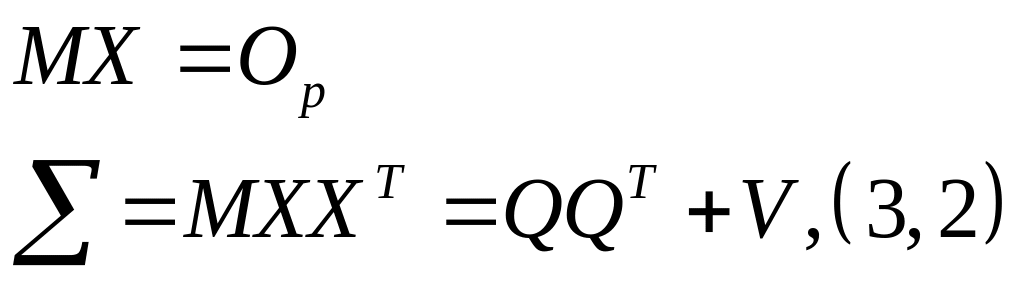
Пример: интерпретации модели факторного анализа в терминах так называемых “интеллектуальных тестов”.

Пусть Х - отклонение оценки в баллах данной ν – му (ν = ) индивидууму на экзамене по j – му тесту от некоторого среднего уровня( j = ) .

Естественно предположить, что в качестве наблюдаемых общих факторов f ,f ,...,f , от которых будут зависеть оценки индивидуумов по всем p-тестам взяты, например, такие факторы как:

• Характеристика общей одаренности - f ,

• характеристика математических способностей - f ,

• характеристика технических способностей - f ,

• характеристика гуманитарной способности - f 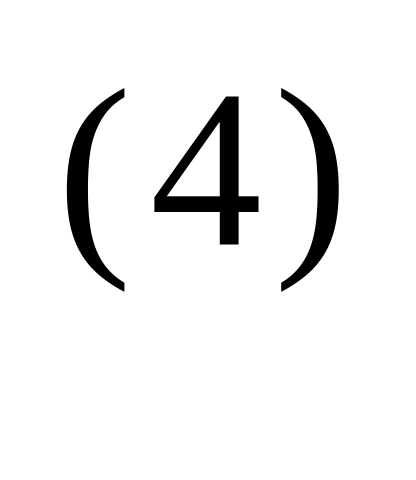и т.д.

Соотношения (3.1) и (3.1’) формально воспроизводят запись модели множеств регрессии, в которой под f ,f ,...,f понимают объясняющие переменные. Однако, в регрессивном анализе f - измеряются на статистически исследованных объектах, в то время как в моделях факторного анализа f ,f ,...,f не являются непосредственно наблюдаемыми.

При разработке модели ФА исследователю приходится решать следующие вопросы:

• Существования модели (при каких , p, p’ предположение о существование связей вида (3.1) является обоснованным и содержательным. При каких имеет место (3.2).

• единственности (идентификации) модели

• алгоритмическое определение параметров модели( нахождение матриц Q иV при некоторых предположениях)

• статистическое оценивание параметров модели

• статистическая проверка ряда гипотез, связанных с природой модели

• построения статистических оценок для значений общих факторов.

Существует тесная связь методом главных компонент и методом ФА. Эти методы должны давать близкие результаты в тех случаях, когда главные компоненты строятся по корреляционным матрицам исходных признаков, а остаточные дисперсии ν = Du сравнительно малы.