29

“Многомерные статистические методы”                                                                              

Часть I. Методы многомерной классификации Пункт 1. Вводный пример

Классификация семей по анализируемой структуре расходов за летний период по двум показателям:

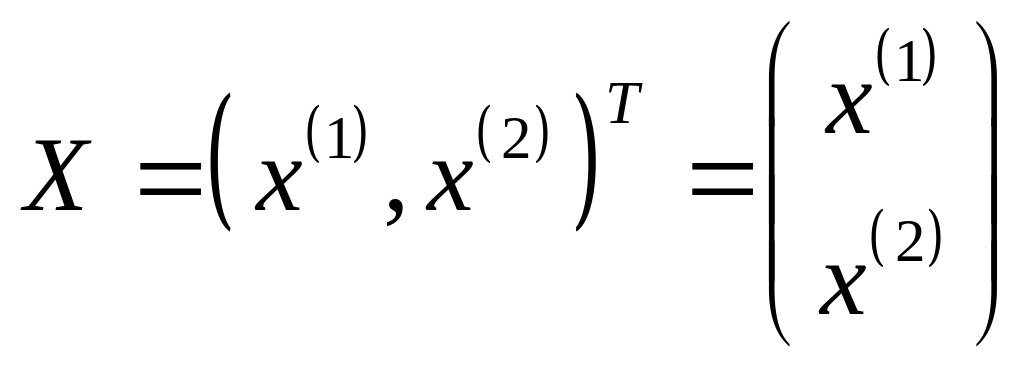х ⁽²⁾

Таблица 1

	Х (1)	х (2)
Х1	2	10
Х2	4	7
Х3	8	6
Х4	12	11
Х5	13	9

х ⁽¹⁾ - расходы на отдых;

х ⁽²⁾ - расходы на питание; х ⁽¹⁾

число семей n = 5.

Меру близости будем характеризовать евклидовом расстоянием:

Матрица расстояний:

Матрица квадратов расстояний:

Этапы разбиения:

1. Сначала считаем, что каждый объект образует самостоятельный кластер:

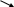S_k⁽¹⁾ (k) ={ X_k } = S(k) = S_k k=1,…,5

    Номер объектов в кластере

Номер кластера

X₄ и X₅ наиболее близки, поэтому объединяем их в один кластер, после объединения

получаем 4 кластера:

2. Надо ввести меру расстояния между кластерами, так чтобы

              Этому требованию  удовлетворяет расстояние, измеряемое по принципу  ближнего  соседа

(расстояние между кластерами, содержащими по одному элементу, было равно расстоянию между этими элементами):

                                                                                                                                                                                                                                                                                                                                                  (*) 

Получаем матрицу расстояний:

Объединяем кластеры:

            После объединения получаем 3 кластера:

3. Вычисляем матрицу расстояний по формуле (*)

Объединяем кластеры:

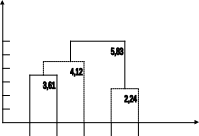
После объединения получаем 2 кластера:

Получаем матрицу расстояний:

       

   

          6

          5

          4

          3

          2

          1

                1 2 3 4 5

Пункт 2. Формы записи исходных статистических данных (исд) Рассмотрим 2 основные формы записи исд:

Имеется n исследуемых объектов О₁, О₂,…, О_n,.

Состояние каждого из которых характеризуется p анализируемыми признаками

 П₁, П₂,…, П_p в каждый из моментов времени t ₁, t₂,…, t _T

 Чаще всего эти моменты берут равноотстоящими, т.е.

  t₂ – t₁ = t₃ – t₂ =…= t_T – t_T-1 = Δt t_k = kΔt , k=1,…,Т

поэтому, не ограничивая общности можно сказать Δt =1, тогда t=1,…,Т

Первая , наиболее распространенная форма представления ИСД, называется матрицей (или таблицей) «ОБЪЕКТ - СВОЙСТВО»

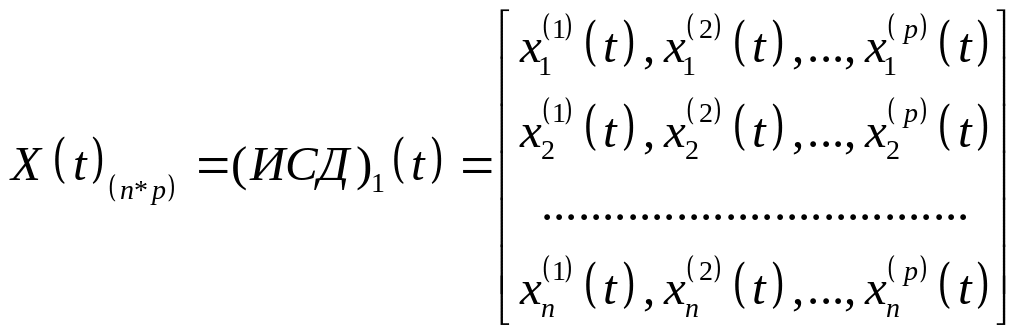      , где t=1,…,Т.                                          (2.1)

x _i^(j)(t) – значение j-ого анализируемого признака объекта О_i в момент времени t

Данные Х(t) определяют пространственно – временную выборку, при формировании которой статическому обследованию подвергается n объектов размещенных в пространстве), причем на каждом объекте регистрируются р характеризующих его признаков в последовательные моменты времени t.

Очевидно, что запись Х(t) определяет целую последовательность (Т штук) матриц. Данные этого вида содержат n реализаций р- мерного временного ряда

{ x ⁽¹⁾(t), x ⁽²⁾(t),…, x ^(p)(t)}

Частные случаи:

1. когда мы имеем т.н. одномоментные наблюдения (Т =1), то получаемая выборка является пространственно- статической:

        (2.2)

2. при Т > 1 и n=1 (обследуется единственный объект). Речь идет о единственной траектории р- мерного временного ряда { x ⁽¹⁾(1), …, x ^(p)(1)},…,{ x ⁽¹⁾(T),…, x ^(p)(T)};

3. при Т > 1 и n = р =1 имеем реализацию одного временного ряда x (1),x (2),…, x (T).

В ряде ситуаций (например, когда ИСД получаются с помощью соц. опросов, анкет) элементами первичного наблюдения является не состояние i -ого объекта в момент времени t, а характеристика γ_ij (t) попарного сравнения двух объектов ( или признаков) с номерами i и j, отнесенные к моменту времени t.

Если γ_ij (t) – результат сопоставления О_i и О_j, то это мера сходства (различия) О_i и О_j, мера их связи и взаимодействия в каком- либо процессе ( поток продукции из отрасли i в отрасль j ), геометрическое расстояние между объектами, отношениями предпочтения:

γ_ij может быть мерой взаимной коррелированности (т.е. коэффициентом корреляции и ковариации) признаков x ⁽ⁱ⁾и x ^(j)

В большинстве случаев имеет место γ_ij = γ_ji .

В этой ситуации в качестве массива ИСД имеем временную последовательность квадратных матриц попарных сравнений n*n ( если рассматриваются характеристики попарного сравнения объектов) или р*р (если рассматриваются характеристики попарного сравнения признаков):

m = n или p, t = 1,…,T.                                                                                                                             (2.3)

В статическом варианте (Т=1) имеем одну матрицу парных сравнений:

                                                                                                                                                                                                                                                                                                                                       (2.4)

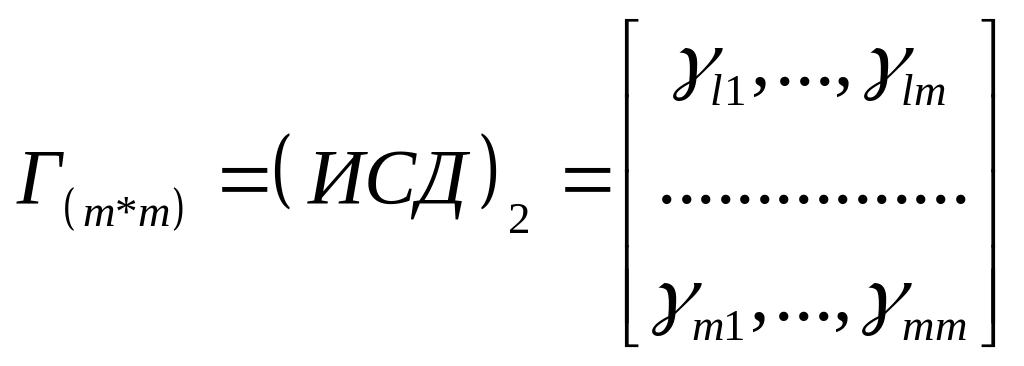
При наличии заданной метрики в пространстве объектов и в пространстве признаков от формы записи (ИСД)₁ можно перейти к (ИСД)₂ . Обратный переход без дополнительных предположений и специальных методов, вообще говоря, невозможен.

В дальнейшем мы не будем рассматривать временной вариант записи ИСД (2.1) и (2.3), а ограничимся рассмотрением статического варианта задания ИСД (2.2) или (2.4), подразумевая при этом:

• каждый из объектов О_i (i =1,…,n) задан соответствующей строкой матрицы (2.2), т.е. вектором Х_i = (x _i⁽¹⁾, x _i⁽²⁾,…, x _i^(p)) либо геометрическая структура их попарных расстояний (близостей) задана матрицей Г_(m*m) (2.4);

• а налогично будем считать, что каждый из признаков П_к к=1,…,р, задается соответствующим столбцом матрицы (2.2):

При наличии вероятностной модели исследуемого процесса, т.е. при вероятностной интерпретации ИСД, совокупность векторов Х_i ,i =1,…,n                                                              (2.5),

рассматривается как выборка объема n из некоторого р- мерного распределения с функцией распределения F(z) = F( z₁,…., z_p ; θ₁,…, θ_s) неизвестной или известной полностью или известной с точностью до некоторых параметров.

Иными словами вектора Х_i ,i =1,…,n, (2.5) интерпретируются как как n реализаций (наблюдений) р- мерного случайного вектора ξ = (ξ⁽¹⁾, ξ⁽²⁾ ,…,ξ⁽ⁿ⁾ )^T                                                                    (2.6)

Напомним, что в статистике, в зависимости от контекста допускается двойной подход к понятию «выборка»:

• с одной стороны «выборка объема n» - это фактически наблюденные в этом эксперименте n значений исследуемой р- мерной случайной величины, т.е. конкретные наборы чисел.

• с другой стороны «выборка объема n» - это совокупность n p- мерных случайных величин вида (2.6)

Вообще, следует помнить, что математические понятия генеральная совокупность, вероятностное пространство, случайная величина, закон распределения в определенном смысле являются синонимами. Вследствие этого синонимами являются понятия «выборка из генеральной совокупности», «выборка из распределения F(z)».

Компоненты векторов Х_i ,i =1,…,n, (2.5) могут соответствовать трем типам данных:

1. Количественные переменные обладают свойством упорядоченности и над ними можно производить арифметические действия (например, денежный доход, объем ВВП, число детей в семье, численность работников предприятия и т.д.)

2. Ранговые (порядковые) позволяют упорядочить объекты по степени проявления в них некоторого свойства. Их значения упорядочены ( их можно перенумеровать натуральными числами), но над ними нельзя производить арифметические действия (например, уровень жилищных условий, квалификационный разряд рабочего, уровень образования сотрудника)

3. Качественные (классификационные, номинальные) позволяют разбить совокупность обследуемых объектов на их поддающиеся упорядочиванию однородные классы (например, пол, профессия, мотив миграции, отрасль промышленности). Им можно поставить в соответствие числа, но они не могут отражать какой- либо упорядоченности значений качественной переменной. Исключением является дихотомные переменные, 2 значения которых ( обычно это 0 и 1) можно считать упорядоченными.

Желательно, чтобы ИСД соответствовали одному типу переменных. В противном случае разные типы переменных сводят к какому-то одному.

Например, область значений количественных переменных разбивают на интервалы, которые нумеруются числами натурального ряда. Ранговые переменные автоматически становятся качественными, если не учитывать упорядоченности их значений.