50

Часть II. Методы снижения размерности исследуемого многомерного признака Пункт 1. Сущность задач снижения размерности

В статистических исследованиях часто приходиться сталкиваться с ситуациями, когда общее число p признаков, регистрируемых на каждом из n обследуемых объектов (стран, городов, предприятий, семей, индивидуумов, технических систем и т.д.) очень велико – порядка100 и более.

Однако имеющиеся наблюдения , следует подвергнуть статистической обработке, осмыслить, ввести в базу данных и т.д.

Е стественно, желание исследователя представить каждое из наблюдений X_i в виде вектора , где p′«p бывает, в частности, обусловлено следующими причинами:

• необходимость наглядного представления (визуализации) исходных данных, что достигается их проецированием на специальным образом подобранное трёхмерное пространство (p′=3), плоскость (p′=2) или прямую (p′=1);

• стремление к лаконизму исследуемых моделей, вызванному необходимостью упрощения счёта и интерпретации полученных данных;

• необходимость существенного сжатия объёмов хранимой статистической информации без видимых потерь в её информативности.

Новые (вспомогательные) признаки могут выбираться из числа исходных или определяться по совокупности исходных признаков (например, как их линейная комбинация).

Имеются следующие основные типы предпосылок, обуславливающих возможность перехода от большого числа p исходных показателей состояния анализируемого объекта к существенно меньшему числу p′ наиболее информативных переменных:

• дублирование информации, доставляемой сильно взаимосвязанными признаками;

• неинформативность признаков, мало меняющихся при переходе от одного объекта к другому (малая вариабельность признаков);

• возможность агрегирования (т.е. простого или взвешенного суммирования) некоторых признаков.

При формировании новой системы признаков к ним предъявляются разного рода требования: наибольшая информативность, взаимная некоррелированность, наименьшее искажение геометрической структуры множества исходных данных и т.д.

Формальное описание перехода от исходного набора признаков к новому ”наилучшему” таково:

Пусть                                                                                  (1.1)

– некоторая p′ – мерная (p′≤p) функция от исходных переменных: F_p′ ={F_p′ (x)}-класс допустимых преобразований, F_p′ : XZ_p′ ( при p′ =p индекс p′ внизу будем опускать), а J_p′(F_p′ (x))-некоторый функционал –определённым образом заданная мера информативности p′- мерной системы признаков.

Тогда задача заключается в нахождении такого набора признаков , что при фиксированном p′ J_p′ (F(x))=extr{J_p′ (F_p′ (x))}(1.2), Z_p′  F_p′.

Тот или иной вариант выбора меры информативности J_p′ (Z(x)) и класса допустимых преобразований F приводит к конкретному методу снижения размерности: методу главных компонент, факторному анализу и т.д. При этом, большинство методов снижения размерности базируется на линейных моделях, т.е. класс допустимых преобразований F(x)- это класс линейных преобразований исходных переменных.

Пункт 2. Метод главных компонент

§2.1 Основные понятия и определения

Во многих задачах обработки многомерных наблюдений, в частности задачах классификации, исследователей интересуют те признаки, которые обнаруживают наибольшую изменчивость (пример, при классификации “семей-потребителей”). С другой стороны, для описания состояния объекта не обязательно непосредственно использовать замеренные на нём признаки (пример: определение специфики фигуры при покупке одежды).

Эти соображения положены в основу того линейного ортонормированного преобразования исходной системы признаков X = (x⁽¹⁾ ,…,x^(p) ), которое приводит к выделению так называемых главных компонент. В этом случае из (1.1) имеем Z=F(x)=LX(2.1), где

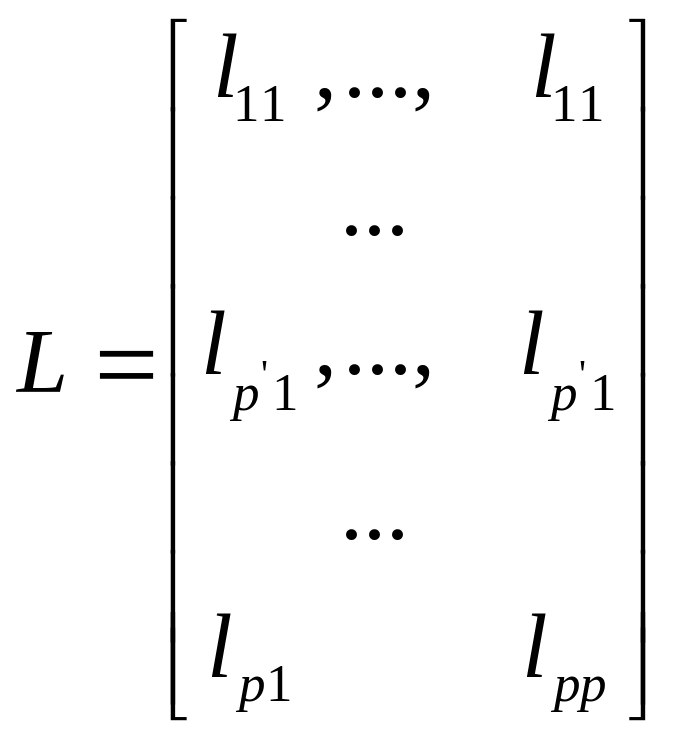                                                                                                                                                           (2.2) матрица порядка (pp), строки которой удовлетворяют условиям ортонормированности:

                                                                                                                

                             

                                                                                                                                                             (2.3)

Здесь и дальше в виде исключения мы будем изначально считать вектора строк матрицы L

- векторами-строками.

Тогда при p'<p: Z_p' =F_p' (x)= L_p' X,                                                                                                 (2.1')

где

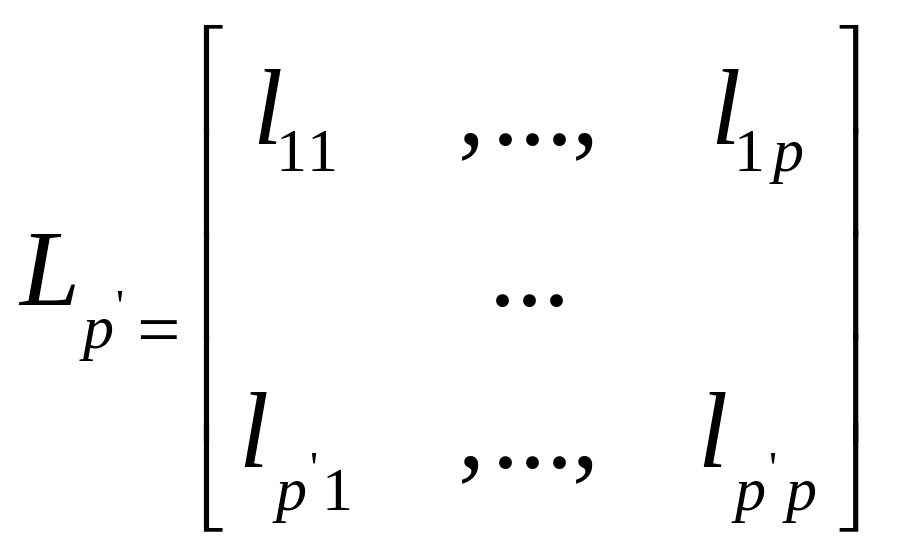                                                                                                                              (2.2’)

- матрица порядка (p'p), составленная из p' первых строк матрицы L (2.2), такая, что в

соответствии с (1.2) J_p' ( )=max J_p' (Z_p' =L_p' X) (2.4), а L_p' F_p'.

Явный вид функционала (2.4) будет указан ниже. F_p' -совокупность матриц (2.2). Полученные таким образом переменные и называются      главными

компонентами вектора X.

В рамках вероятностно-статистического подхода мы полагаем анализируемый признак

X = (x⁽¹⁾ ,…,x^(p) ) случайной величиной, имеющей p-мерное распределение, с вектором средних

MX = a=(a⁽¹⁾ ,…,a^(p) ), где a^(s) = Mx^(s), , и матрицей ковариации

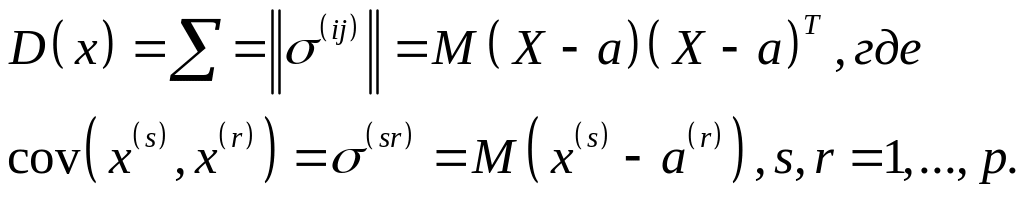
Тогда исследуемые наблюдения , понимаются как выборка из

указанного распределения и используются для получения оценок â и вектора a и матрицы Σ, если последние не известны. Не ограничивая общности, в дальнейшем будем считать, что вектор средних a=0. Этого можно добиться центрированием координат вектора X x^(s) , координат a^(s) вектора a, или (в статистической практике) их выборочными несмещёнными оценками

При этом, как известно, матрица ковариации центрированных переменных снова будет равна

Σ=║σ^(sr)║ (элементы σ^(sr) остануться прежними).

Дадим определение главных компонент и тем самым зададим алгоритм их нахождения.

Определение 1. Первой главной компонентой z⁽¹⁾(x) исследуемой системы показателей

(x⁽¹⁾ ,…,x^(p) )=X, называется такая нормированная центрированная линейная комбинация (НЦЛК)

этих показателей, которая среди всех прочих НЦЛК этих показателей обладает

наибольшей дисперсией.

Определение 2. K-ой главной компонентой z^(k)(x) исследуемой системы показателей

x⁽¹⁾ ,…,x^(p) )=X, называется такая нормированная центрированная линейная комбинация(НЦЛК)

этих показателей, которая не коррелированна с k-1 предыдущими главными компонентами

z⁽¹⁾(x) ,…, z^(k-1)(x) и среди всех прочих НЦЛК (не коррелированных с z⁽¹⁾(x) ,…, z^(k-1)(x))

обладает наибольшей дисперсией.

Выбор такого алгоритма получения главных компонент, а также выбор меры информативности

J_p' (2.4), как будет показано ниже, обусловлен некоторыми свойствами определённых таким

образом главных компонент.

Замечание. Использование метода главных компонент наиболее естественно и плодотворно

в тех случаях, когда все признаки x^(s) , , имеют общую физическую природу и

соответственно измерены в одних и тех же единицах: структура бюджета времени индивидуумов

(все x^(s) - в единицах времени), структура потребления семей (все x^(s) в денежных

единицах), антропологические исследования (все x^(s) – единицы длины).

Если же признаки x^(s) измерены в разных единицах, то в подобных ситуациях исследователь

должен предварительно перейти к вспомогательным безразмерным признакам

Тогда ковариантная и выборочная ковариантная

матрицы будут являться коррелированной и выборочно коррелированной матрицам .