§2.5. Геометрическая интерпретация и оптимальные свойства главных компонент

Всякий переход к меньшему числу переменных осуществляется с помощью линейного преобразования и взятия p’ новых переменных.

Такой переход можно рассматривать как проекцию исходных наблюдений в пространство размерности , натянутое на координатные оси , где

, - аналитическая форма записи

, - матричная форма записи

Пример:

Рассмотрим двумерное нормальное распределение с параметрами ,

Тогда показатели экспоненты для плотности:

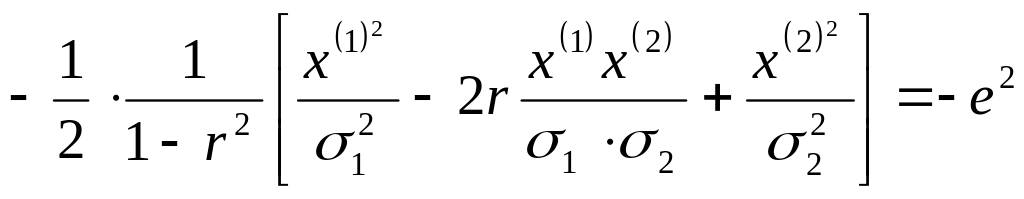
Здесь мы производим преобразование координат путем поворота осей координат:

( и распределены нормально, но независимо. Чем больше (ближе к 1), тем теснее группируются наблюдения возле оси ).

(если , то новая переменная , следовательно, мы перешли к некоррелируемым компонентам. После такого преобразования _, имеют двумерное нормальное распределение, но являются независимыми.

§2.5.1 Свойство наименьшей ошибки «автопрогноза» или наилучшей самовоспроизводимости

Можно показать, что с помощью первых главных компонент ,…, , исходных признаков ,…, достигается наилучший прогноз этих признаков среди всех прогнозов, которые можно построить с помощью линейных комбинаций исходных признаков.

В нашей ситуации мы хотим заменить исследуемый р-мерный вектор наблюдений на вектор меньшей размерности , в котором линейной комбинацией исходных признаков, теряя при этом не слишком много информации.

Информативность вектора Y зависит от того, в какой степени линейных комбинаций дают возможность «реконструировать» р исходных измеряемых на общих признаках .

Ошибку прогноза Х по Y будем обозначать и определять как некоторую функцию от так называемой остаточной дисперсионной матрицы вектора Х при вычитании из него наилучшего, в смысле наименьших квадратов, прогноза по Y:

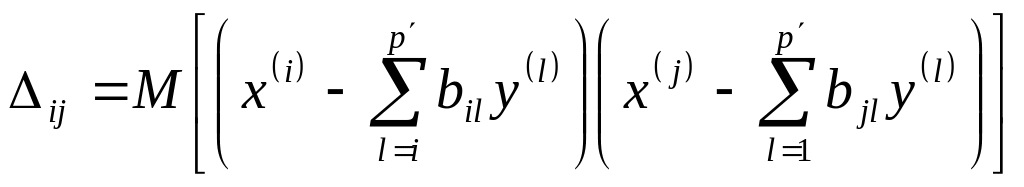                                           (2.26)

Где - наилучший, в смысле наименьших квадратов, прогноз по ,…, .

Были рассмотрены 2 вида функции f:

                                             (2.27)

- евклидова норма матрицы                                       (2.28)

Доказано, что функции и одновременно достигают максимума тогда и только тогда, когда ,…, являются главными компонентами, то есть:

,…, .

При этом (2.27) и (2.28) превращаются соответственно в:

,                                                                       (2.27’)

.                                                                     (2.28’)

Где – последние собственных чисел исходной матрицы (или ее выборочной оценки ; в этом случае (2.27’) и (2.28’) будут приближаться равенствами).

Вернемся к примеру §. 2.3.

В соответствии с результатом примера возьмем в качестве единственной вспомогательной переменной первую главную компоненту:

тогда из (2.26) наилучший прогноз для , , при p=3 имеет вид , i=1,2,3.