§2.2. Вычисление главных компонент.

Из (1.5) и определения главных компонент (2.1) следует, что для вычисления первой

главной компоненты следует решить оптимизационную задачу

                                                                                                                                                                   (2.5)

где )- первая строка матрицы L.

X =(x⁽¹⁾ ,…,x^(p) )^т, т.к. MX=0 (случайные величины x⁽¹⁾ ,…,x^(p) –центрированы) и MXX^т=∑, то

(2.6) и (2.6) может быть записано в виде

                                                                                                                                                                (2.7)

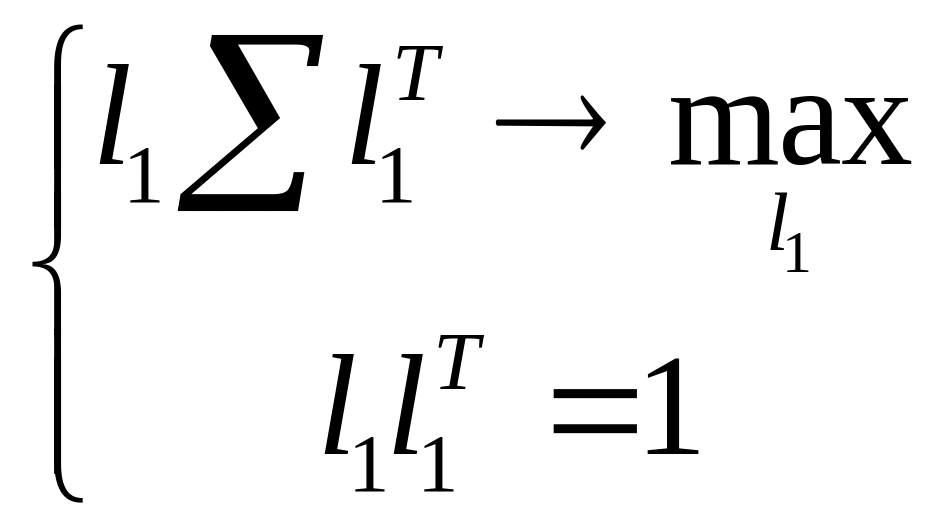
Из (2.7), вводя функцию Лагранжа, получим

                                                                                                                      (2.8)

(значит, функция p+1 переменной).

Дифференцируя её по переменным , из (2.8) получим вектор-столбец

частных производных .                                                                                      (2.9)

Приравнивая первые частные производные (2.9), будем иметь систему из p линейных

уравнений относительно неизвестных ( ):

                                                                    ,                                                           (2.10)

где - единичная матрица размерности (p p), =(0,0,…,0)^T – p-мерный вектор-столбец

из нулей. Решение системы(2.10), которое мы хотим найти, должно быть ненулевым:( =1).

Для того чтобы существовало такое решение, матрица системы(2.10) должна быть вырожденной, т.е. её определитель должен быть равен нулю: =0.                         (2.11)

Уравнение (2.11) называется характеристическим уравнением матрицы . Левая часть уравнения (2.11) представляет собой многочлен степени p относительно переменной λ.

1. Линейные пространства.

a, b, V, αR, (a+b)V, αaV,0V, -aV

коммутативность, дистрибутивность.

Линейно независимые системы векторов. База. Размерность. Конечномерные

пространства. Изоморфизм.

векторные пространства строк.

Базы и связанны невырожденной матрицей H,

в базе e

в базе e

2. Линейные преобразования.

V_n-n мерное действительное линейное пространство.:V_k→V_n(не обязательно биекция)

aφ=a,φ-линейно, если (a+b ) φ=aφ+bφ и (αa) φ =α(aφ). Если e_1,e₂,,e_n-база, то φ

однозначно определено образами векторов e₁φ_,e₂φ,,e_nφ.

Существует взаимнооднозначное соответствие между всеми линейными

преобразованиями пространства V_n и всеми квадратными матрицами А порядка n (зависящее от

выбора базы):e=Ae.

Для базы - матрица А. А и А связаны через матрицу :

Ранг преобразования. Суммы и произведения линейных преобразований и умножение их на

число:

Собственные векторы линейного пространства. Собственные значения.

- A в базисе e_1,,e_n

Cобственные значения не зависят от базиса.

3. Евклидовы пространства.

E_n: V_n -векторное n-мерное действительное пространство.

a и b – (a,b,)=(b,a (a+b,c)=(ac,bc),(αa,b)=α(a,b).

Любое V_n можно сделать евклидовым E_n,если определить скалярное произведение:

и - коэффициенты

представления векторов a и b в некотором базисе e_1,e₂,,e_n.

Всякая ортогональная система ненулевых векторов линейно независима.

Процесс ортогонализации. Всякое евклидово пространство обладает ортогональными базами,

причём любой ненулевой вектор входит в состав хотя бы одной из таких баз. База

называется ортонормированной, если (e_i,e_i)=1, ,( e_i,e_j)=0, i≠j.

Всякое евклидово пространство обладает ортонормированными базами.

4. Ортогональные матрицы, ортогональные преобразования.

Матрица перехода от одной ортонормированной базы E_n к другой является ортогональной:

H′H=E, H′=H^-1.

5. Симметричные преобразования в E_n ;

Справедливы следующие утверждения (см. на обороте страницы 50)

Из этих утверждений мы выведем ряд свойств симметрических матриц.

Замечание: Уравнения вида (2.11) возникают при нахождении собственных векторов линейного преобразования φ действительного линейного пространства V_R : если существует вектор x0 такой, что (x)_оx, где _о  некоторое вещественное число, называющееся собственным значением преобразования , то он называется собственным вектором линейного преобразования .

Л инейное преобразование  в разных базисах может задаваться различными матрицами (pp), но для любой такой матрицы А собственные значения линейного преобразования  и только они будут являться корнями характеристического уравнения.

 подобная матрица.