По методу наименьших квадратов имеем

,

откуда

,

i=1,2,3.

; - берутся из матрицы ковариаций.

Отсюда

В качестве относительной ошибки прогноза исходного признака по первой главной компоненте будем использовать величину:

Суммарная относительная ошибка подсчитывается по формуле:

§2.5.2. Свойства наименьшего искажения геометрической структуры множества исходных р-мерных наблюдений при их проектировании пространства р’ первых главных компонент:

(без доказательства)

1. Сумма квадратов расстояний от исходных наблюдений 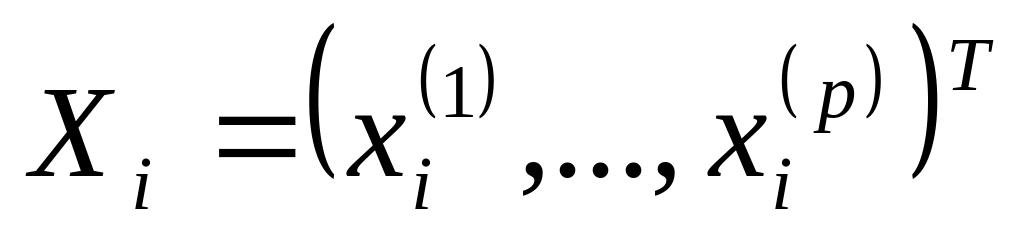до подпространства, натянутого на р’ первых главных компонент, наименьшая относительно всех других подпространств размерности р’, полученных с помощью произвольных линейных преобразований исходных координат.

2. среди всех подпространств заданной размерности , полученных из исходного пространства с помощью произвольно линейного преобразования исходных координат, в подпространстве, натянутом на первые p’ главных компонент, наименее искажается сумма квадратов расстояний между всевозможными парами точек рассматриваемых наблюдений.

Поясним это:

Обозначим

- сумма квадратов евклидовых расстояний

После проецирования точек в р’-мерное пространство, определяемое первыми р’ компонентами линейного преобразования:

Можно показать, что при

Кроме того,

где – вектор первых р’ главных компонент.

(iii) Среди всех подпространств заданной размерности р’ , полученных с помощью линейного преобразования исходных координат ,…, в пространстве, натянутом на р’ первых главных компонент наименее искажаются расстояния от рассматриваемых точек наблюдений до их общего центра тяжести.

§2.6Статистические свойства выборочных главных компонентов

Вероятно-статистический подход заключается в том, что мы по некоторой части генеральной совокупности ( по выборке) делаем выводы о генеральной совокупности( о распределении из которых берем выборки).

Итак, в случае, когда неизвестно теоретическое распределение (неизвестно ковариационная матрица ∑ )многомерного вектора Х=Х ,Х ,...,Х , мы по наблюдениям Х1, Х2,...,Хn ; Хv =X ,...,X .строим выборочную ковариационную матрицу , находим ее собственные значения 1,..., n являющиеся оценками теоретических собственных значений λ1... λp, и собственного вектора j соответствующего значениям J . J= Приведем без доказательства несколько утверждений, справедливых в случае, когда все теоретические значения λj различны.

1. Собственные значения J ; J = 1...p, и соответствующие им собственные вектора j выборочной ковариационной матрицы являются оценками максимального правдоподобия для соответствующих теоретических характеристик.(т.е. для λj и Lj соответственно) и обладают всеми хорошими свойствами этих оценок(состоятельность, асимптотическая эффективность). Если среди характеристических корней λj встречаются одинаковые, то оценки максимального правдоподобия определяются несколько иначе. Следовательно, выбор главных компонент 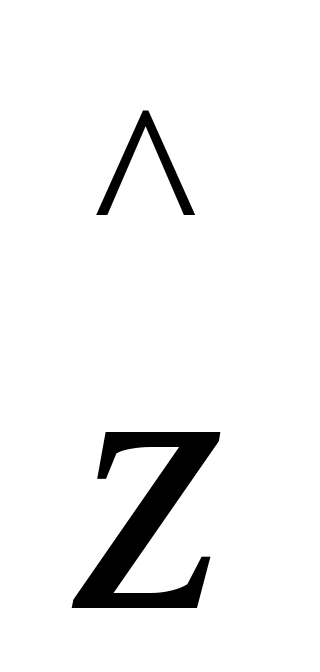j = j X Можно интерпретировать, как оценки теоретических главных компонент = j X

2. Случайная величина 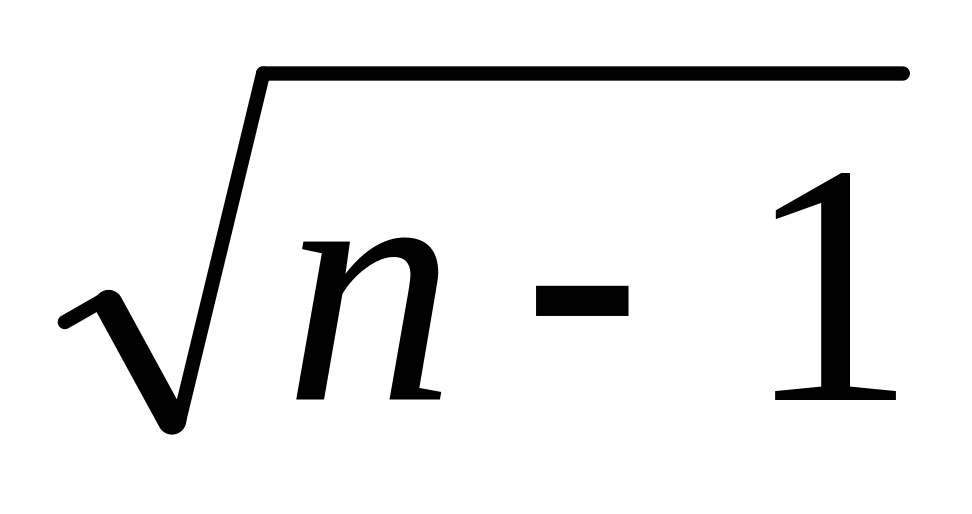( - λj) , J= , при n→ ∞ асимптотически нормальна с параметрами(0; λj√2). Используя этот факт можно построить доверительный интервал для собственных значений λj.

Подведем итоги

Главные компоненты являются полезным инструментом в задачах “ автопрогноза” большого числа анализируемых показателей по сравнительно малому числу вспомогательных переменных, визуализации многомерных данных, построении типообразующих признаков, при классификации многомерных объектов, при предварительном анализе геометрической и вероятностной природы исходных данных.