
- •Вопросы к экзамену по математическому анализу (2 семестр) Вопросы по теме «Неопределенный интеграл»
- •1. Интегралы вида
- •2. Интегралы вида
- •3. Интегралы вида
- •Вопросы по теме «Определенный интеграл»
- •Вопросы по теме «Функции нескольких переменных»
- •Образец экзаменационного билета
- •Часть 1 (на оценку 3). Засчитывается правильный выбор ответа из предложенных справа в таблице, но только при наличии решения.
- •Часть 2 (на оценку 4 и 5, ответ устный, не исключаются дополнительные вопросы по определениям, теоремам).
Вопросы по теме «Функции нескольких переменных»
Понятие функции нескольких переменных (привести примеры функции 2-х, 3-х, п переменных), ее область определения, изображение области определения для функции двух переменных. График функции 2-х переменных.
Если
каждой точке М(x1,
x2,
…,xn)
множества D
евклидова пространства Rn
по некоторому закону ![]() поставлено
в соответствие единственное действительное
число u,
то говорят, что на множестве D
задана функция нескольких
переменных u=
(x1,x2,…,xn) или
u=
(M).
поставлено
в соответствие единственное действительное
число u,
то говорят, что на множестве D
задана функция нескольких
переменных u=
(x1,x2,…,xn) или
u=
(M).
Множество D при этом называют областью определения функции (M) и обозначают D( ); переменные x1,x2,…,xn называются независимыми переменными или аргументами функции, а число u – зависимой переменной.
Геометрическим изображением (графиком) функции двух переменных z = f ( x, y )является множество точек P ( x, y, z) в трехмерном пространстве Oxyz, координаты которых удовлетворяют уравнению z = f ( x, y ).
Графиком функции непрерывных аргументов, как правило, является некоторая поверхность в пространстве Oxyz, которая проектируется на координатную плоскость Oxy в область определения функции z= f ( x, y ).

Линии и поверхности уровня, примеры. Для функции z = x2 + y2 –6x +4y + 25 запишите уравнение линии уровня, проходящей через точку Р(1, –4). Постройте ее.
Линией уровня функции z= (x,y) называется множество точек области определения функции, в которых эта функция принимает принимает одно и то же значение С. Уравнение линий уровня (x,y)=C.
Поверхностью уровня функции u= (x,y,z) называется множество точек области определения функции, в которых эта функция принимает одно и то же значение С. Уравнение поверхностей уровня (x,y,z)=C.
Определение частного приращения ФНП, частных производных 1-го, 2-го, 3-го и т.д. порядков.
Частной
производной
![]() функции u=
(x1,x2,…,xn)
по переменной x1
в фиксированной точке M(x1,x2,…,xn)
называется предел отношения частного
приращения
функции u=
(x1,x2,…,xn)
по переменной x1
в фиксированной точке M(x1,x2,…,xn)
называется предел отношения частного
приращения
![]() x1u
функции к приращению
аргументa
x1 при
-->0
(сли этот предел существует):
x1u
функции к приращению
аргументa
x1 при
-->0
(сли этот предел существует):
![]()
Частными производными второго порядка от функции z=f(x,y) называются частные производные от ее частных производных первого порядка f ‘x(x,y), f ‘y(x,y):
![]() = (f
‘x(x,y))’x.
= (f
‘x(x,y))’x.
![]() =
(f ‘y(x,y))
’y.
=
(f ‘y(x,y))
’y.
![]() = (f
‘y(x,y))
’y,
= (f
‘y(x,y))
’y,
![]() =
(f ‘x(x,y))’x
=
(f ‘x(x,y))’x
Чпроизводные третьего порядка
Физический смысл частных производных 1-го порядка.
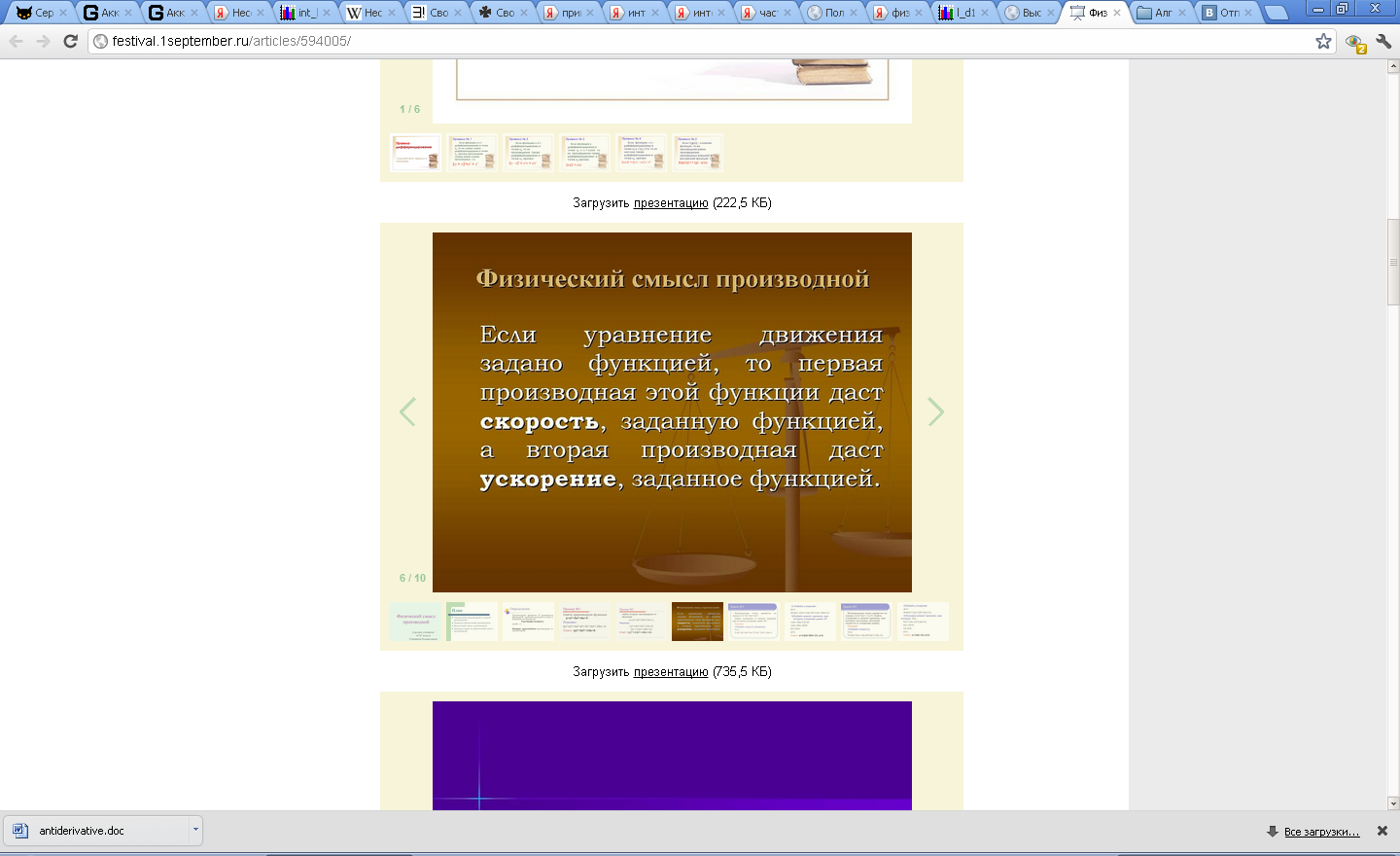
Температура точки стержня ОХ является функцией абсциссы х этой точки и времени t: =f(x,t). Каков физический смысл частных производных
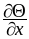 и
и
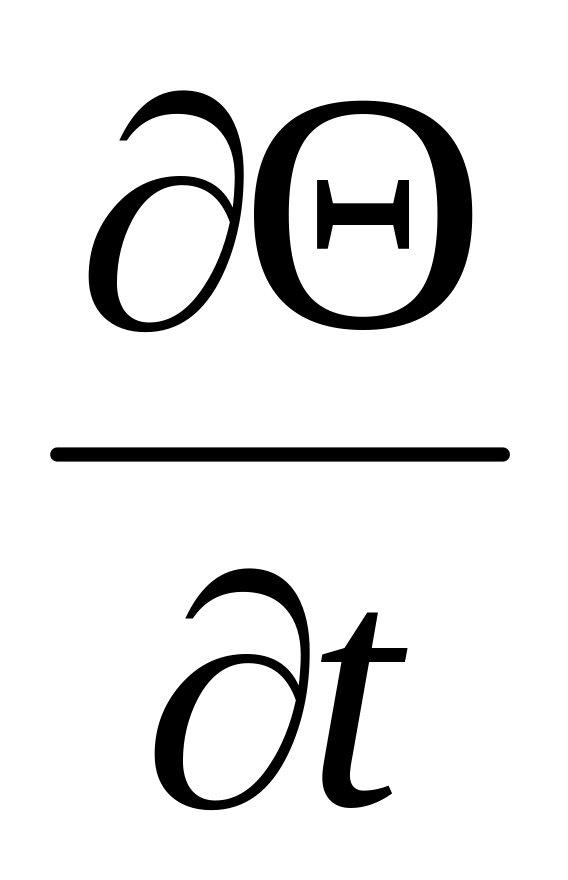 ?
?
Записать площадь S прямоугольника как функцию его основания b и высоты h. Найти
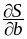 и
и
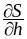 ,
указать их смысл.
,
указать их смысл.
Понятие дифференцируемости ФНП, полного дифференциала, связь между ними. Частные дифференциалы, формула полного дифференциала 1-го , 2-го порядков.
Функция u=f(x1,x2,…,xn) называется дифференцируемой в точке M(x1,x2,…xn), если полное приращение Δu=f(x1+ Δx1, x2+ Δx2,…, xn+ Δxn) – f(x1,x2,…xn) функции в некоторой окрестности этой точки может быть представлено в виде Δu=A1Δx1+ A2Δx2+…+ AnΔxn+o(p),
Где А1,А2 – числа не зависящие от Δx1, Δx2,… Δxn, o(p) – бесконечно малая более высокого порядка по сравнению с p=( Δx12+ Δx22+…+ Δxn2)1/2
Полным дифференциалом du дифференцируемой функции u=f(x1,x2,…xn) называется главная частьполного приращения функции, линейная относительно приращений аргументов Δx1, Δx2,…, Δxn:
du=A1Δ x1+A2Δ x2+…+ AnΔ xn
Если функция дифференцируема в точке (x1,x2,…xn)? То она имеет в этой точке частные производные по каждой переменной, при этом
du= Δ x1 +du/dx2 Δ x 2+du/dxn Δ x3
В силу равенства Δ xi=dxi для независимых переменных , получаем
du= Δ dx1 +du/dx2 Δ dx 2+du/dxn d x3
Слагаемые в правой части равенства называются частными дифференциалами функции u по переменным xi и обозначаются dxiu= dxi. Следовательно полный дифференциал равен сумме частных дифференциалов: du=dx1u+ dx2u+…+ dxnu.
Производная по направлению, градиент, их свойства и связь (с доказательством), физический смысл.
Производная
![]() от
функции u=f(x,y,z)
по направлению вектора а=(ax,
ay,
az
) вычисляется
по формуле
(M0)=
(M0)*cosL+
от
функции u=f(x,y,z)
по направлению вектора а=(ax,
ay,
az
) вычисляется
по формуле
(M0)=
(M0)*cosL+
Линеаризация функции одной и нескольких переменных, ее геометрическая интерпретация, формула линеаризации.
Неявная функция 1-й, 2-х, 3-х и т.д. переменных. Дифференцирование неявных функций. Примеры для функций 1-й, 2-х, 3-х переменных.
Определение точек максимума и минимума ФНП, экстремумов ФНП.
Необходимое условие существования экстремума (*с доказательством), критические точки, их связь с точками экстремума.
Достаточное условие существования экстремума ФНП, частный случай функции 2-х переменных.
Условный экстремум, его геометрический смысл, способы его нахождения.
Наибольшее и наименьшее значения ФНП в замкнутой ограниченной области, условия их существования для ФНП, графический и аналитический методы их нахождения.
Метод наименьших квадратов, его суть и примеры применения (для линейной, квадратичной, показательной функций).
