
- •1.Метрические пространства, неравенство Коши-Шварца.
- •2. Метрические пространства. Основные определения.
- •3.Векторное пространство с нормой. Евклидово пространство, понятие полноты.
- •5. Предел отображения в точке. Свойства отображений, имеющих предел в точке.
- •6.Предел и арифметические операции. Критерии Коши существования предела отображения в точке.
- •7. Предел по множеству. Предел по направлению.
- •8. Непрерывность отображений. Локальные свойства непрерывных отображений.
- •9. Равномерная непрерывность. Глобальные свойства непрерывных отображений.
- •10. Частные производные. Дифференцируемость отображений. Структура матрицы дифференциала.
- •12. Необходимые, достаточные условия дифференцируемости отображений.
- •14. Дифференциал функции нескольких переменных. Инвариантность формы первого дифференциала. Приближенные вычисления.
- •15. Геометрические приложения производной функции нескольких переменных.
- •16. Производные и дифференциалы сложных функций.
- •17. Производные высших порядков явно заданной функции
- •18.Дифференциалы высших порядков
- •19.Формула Тейлора
- •20. Формула Тейлора функции 2х переменных
- •21.Формула Тейлора с остаточным членом в формуле Пеано
- •46. Замена переменных
- •52. Знакопеременные ряды. Абсолютная и условная сходимость рядов.
- •49. Понятие о n-кратных интегралах.
- •48. Геометрические и физические приложения
- •53. Признак Абеля и Дирихле сходимости знакочередующихся рядов.
- •54. Функциональные ряды. Сходимость функциональных рядов.
- •55. Равномерная сходимость функциональных рядов. Условия равномерной сходимости.
- •56. Свойства равномерно сходящихся рядов.
- •57. Степенные ряды. Радиус сходимости. Формула Коши-Адамара.
- •58. Равномерная сходимость степенных рядов. Почленное дифференцирование и интегрирование степенных рядов.
- •59. Разложение элементарных ф-ций в ряд Тейлора (Маклорена)
- •60. Формулы Эйлера.Формула Стирлинга. Применение степенных рядов к решению задач.
58. Равномерная сходимость степенных рядов. Почленное дифференцирование и интегрирование степенных рядов.
Свойства степенных рядов:
Если R
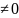 ,то
его сумма непрерывна на интервале
(-R,R)
и его можнопочленно дифференцировать
на всем интервале сход.и для его суммы
имеет места формула:
,то
его сумма непрерывна на интервале
(-R,R)
и его можнопочленно дифференцировать
на всем интервале сход.и для его суммы
имеет места формула:
S‘(x)=
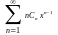 .
Т.о. степенной ряд на интервале сходимости
(-R,R),
R
можно почленно дифф-ть
количество
раз
.
Т.о. степенной ряд на интервале сходимости
(-R,R),
R
можно почленно дифф-ть
количество
раз
Операции почленного дифференцирования и интегрирования на
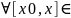 (-R,R)
не изменяют R
степенного ряда.
(-R,R)
не изменяют R
степенного ряда.Степенной ряд
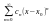 можно почленно интегрировать на любом
отрезке целиком принадлежащем интервалу
сходимости при этом полученный степенной
ряд имеет тот же радиус сходимости что
и исходный ряд.
можно почленно интегрировать на любом
отрезке целиком принадлежащем интервалу
сходимости при этом полученный степенной
ряд имеет тот же радиус сходимости что
и исходный ряд.
59. Разложение элементарных ф-ций в ряд Тейлора (Маклорена)
Пусть ф-я f(x) имеет в окрестности точки x0 производные всех порядков,тогда выражение вида:
f(x)=f(x0)+
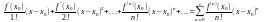 -ряд
Тейлора
-ряд
Тейлора
если х0=0,то ряд Тейлора имеет вид:
f(x)=f(0)+
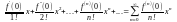 -
ряд
Маклорена.
-
ряд
Маклорена.
Разложение некоторых элементарных ф-ий в ряд Маклорена:
1)Разложение ф-ции ех :
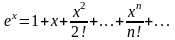 ряд
Маклорена.:
ряд
Маклорена.:
радиус сходимости: R= следовательно ряд абсолютно сходится на всей числовой прямой.
2)Разложение sinx в степенной ряд Маклорена
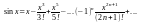
сходится на всей числовой оси
3)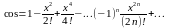 сходится на всей числовой оси
сходится на всей числовой оси
3) f(x) = (1+x)
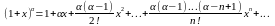 ,
,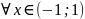 -
биномиальный ряд с показателем .
-
биномиальный ряд с показателем .
 ,|х|<1
(
,|х|<1
(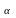 =
-1)
=
-1)
4) Разложение ф-ции ln(1+x)
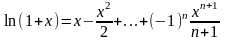
сходится при –1<x<=1
5) Разложение arctgx в степенной ряд Маклорена
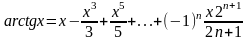 сходится
при -1<=x<=1
сходится
при -1<=x<=1
60. Формулы Эйлера.Формула Стирлинга. Применение степенных рядов к решению задач.
Функция еx обладает важными функциональными св-ом: еx+u = ex eu для любых комплексных х,u ,тогда
Эйлеровы
формулы., связывающие тригонометрические
функции с показательной : eix
= cos
х
+ i
sin
х,
cos
х=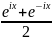 ,
sin
х=
,
sin
х=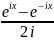
|
Стирлинга
формула-
формула, дающая приближённое выражение
произведения n
первых натуральных чисел (т. н. факториала)
1*2*...*n
= n!,
когда число n
сомножителей велико. Стирлинга
формула
была найдена Стирлинга
формула
устанавливает приближённое равенство:
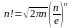
Приложение степенных рядов: с помощью степенных рядов можно вычислить:
1)приближенное вычисление
2)приближенное вычисление интегралов
3)вычисление сумм числовых рядов
4)интегрирование дифф-ых ур-ий
