
- •1.Метрические пространства, неравенство Коши-Шварца.
- •2. Метрические пространства. Основные определения.
- •3.Векторное пространство с нормой. Евклидово пространство, понятие полноты.
- •5. Предел отображения в точке. Свойства отображений, имеющих предел в точке.
- •6.Предел и арифметические операции. Критерии Коши существования предела отображения в точке.
- •7. Предел по множеству. Предел по направлению.
- •8. Непрерывность отображений. Локальные свойства непрерывных отображений.
- •9. Равномерная непрерывность. Глобальные свойства непрерывных отображений.
- •10. Частные производные. Дифференцируемость отображений. Структура матрицы дифференциала.
- •12. Необходимые, достаточные условия дифференцируемости отображений.
- •14. Дифференциал функции нескольких переменных. Инвариантность формы первого дифференциала. Приближенные вычисления.
- •15. Геометрические приложения производной функции нескольких переменных.
- •16. Производные и дифференциалы сложных функций.
- •17. Производные высших порядков явно заданной функции
- •18.Дифференциалы высших порядков
- •19.Формула Тейлора
- •20. Формула Тейлора функции 2х переменных
- •21.Формула Тейлора с остаточным членом в формуле Пеано
- •46. Замена переменных
- •52. Знакопеременные ряды. Абсолютная и условная сходимость рядов.
- •49. Понятие о n-кратных интегралах.
- •48. Геометрические и физические приложения
- •53. Признак Абеля и Дирихле сходимости знакочередующихся рядов.
- •54. Функциональные ряды. Сходимость функциональных рядов.
- •55. Равномерная сходимость функциональных рядов. Условия равномерной сходимости.
- •56. Свойства равномерно сходящихся рядов.
- •57. Степенные ряды. Радиус сходимости. Формула Коши-Адамара.
- •58. Равномерная сходимость степенных рядов. Почленное дифференцирование и интегрирование степенных рядов.
- •59. Разложение элементарных ф-ций в ряд Тейлора (Маклорена)
- •60. Формулы Эйлера.Формула Стирлинга. Применение степенных рядов к решению задач.
1.Метрические пространства, неравенство Коши-Шварца.
Метрические пространства.
Множество
х
для которого задана функция
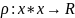 со свойствами:
со свойствами:
1)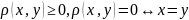
2)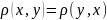
3)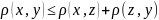 ,
то функция называется метрическим
пространством, а
,
то функция называется метрическим
пространством, а
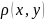 удовлетворяет свойствам 1-3, называется
метрикой этого пространства. Покажем
что пространство
удовлетворяет свойствам 1-3, называется
метрикой этого пространства. Покажем
что пространство
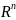 метрическое, если метрика задана
формулой
метрическое, если метрика задана
формулой
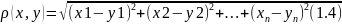 .
Свойства 1-2 очевидны, покажем (пространство)
справедливость 3-го свойства. Для этого
в формуле
.
Свойства 1-2 очевидны, покажем (пространство)
справедливость 3-го свойства. Для этого
в формуле
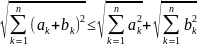 (1.3)
будем считать, что
(1.3)
будем считать, что
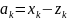 ;
;
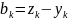 ,
тогда
,
тогда
 ,
отсюда
тогда получим
,
отсюда
тогда получим
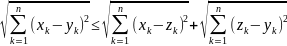 -это и есть как рассматрив.:
-это и есть как рассматрив.:
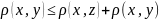 -
неравенство треугольников. Мы показали,
что
c
(1.4) является метрическим пространством.
Из (1.4) и
-
неравенство треугольников. Мы показали,
что
c
(1.4) является метрическим пространством.
Из (1.4) и
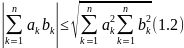 -неравенство
коши-шварца
следует свойство:
-неравенство
коши-шварца
следует свойство:
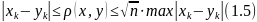
Неравенство коши-шварца. -
Лема:
для того, чтобы (1.2) имело место, необходимо
и достаточно чтобы
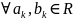 .
Следствие: из (1.2) следует, что
.
Следствие: из (1.2) следует, что
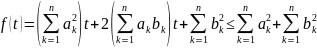 при t=1
при t=1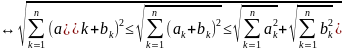 (1.3)
(1.3)
2. Метрические пространства. Основные определения.
Метрические пространства.
Множество х для которого задана функция со свойствами:
1)
2)
3)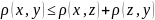 ,
то функция называется метрическим
пространством, а
удовлетворяет свойствам 1-3, называется
метрикой этого пространства. Покажем
что пространство
метрическое, если метрика задана
формулой
,
то функция называется метрическим
пространством, а
удовлетворяет свойствам 1-3, называется
метрикой этого пространства. Покажем
что пространство
метрическое, если метрика задана
формулой
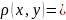
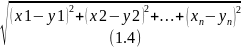 .
Свойства 1-2 очевидны, покажем (пространство)
справедливость 3-го свойства. Для этого
в формуле
(1.3)
будем считать, что
;
,
тогда
,
отсюда
тогда получим
-это и есть как рассматрив.:
-
неравенство треугольников. Мы показали,
что
c
(1.4) является метрическим пространством.
Из (1.4) и
-неравенство
коши-шварца
следует свойство:
.
Свойства 1-2 очевидны, покажем (пространство)
справедливость 3-го свойства. Для этого
в формуле
(1.3)
будем считать, что
;
,
тогда
,
отсюда
тогда получим
-это и есть как рассматрив.:
-
неравенство треугольников. Мы показали,
что
c
(1.4) является метрическим пространством.
Из (1.4) и
-неравенство
коши-шварца
следует свойство:
ОПР:
Множество
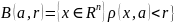 называется открытым шаром. Шар
B(a,б)=V(a,б)
называется ещё дельта-окрестность в
точке a.
называется открытым шаром. Шар
B(a,б)=V(a,б)
называется ещё дельта-окрестность в
точке a.
ОПР
:Точка
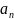 наз.внутренней точкой множества х, где
наз.внутренней точкой множества х, где
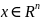 ,
если сущ.дельта-окрестность этой точки
,
если сущ.дельта-окрестность этой точки
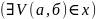 целиком истащал в множестве а. РИСУНОК!
целиком истащал в множестве а. РИСУНОК!
ОПР:
Точка b
называется внешней точкой множества
х, где
если существует б-окрестность в точке
b,
не содерж.точек множества х.
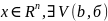 .
ОПР:
точка с называется граничной точкой
множества, если V
ее б-окрестности содержит как внутренние
так и внешние точки множества х.
.
ОПР:
точка с называется граничной точкой
множества, если V
ее б-окрестности содержит как внутренние
так и внешние точки множества х.
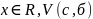 .
.
ОПР :Х называется открытым, состоящее только из внутренних точек.
Теорема:1)объединение
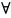 числа
множеств есть открытое множество.
числа
множеств есть открытое множество.
2)пересечение конечного числа открытого множества, является откр.мн-во.
Доказательство:
1)пусть
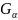 произвольное открытое множество, и
пусть
произвольное открытое множество, и
пусть
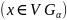 объединённое открытое множество
,
значит х принадлежит хотя бы одному
множеству
.
Значит существует б-окрестность в точке
х целиком лежащая в этом множестве
объединённое открытое множество
,
значит х принадлежит хотя бы одному
множеству
.
Значит существует б-окрестность в точке
х целиком лежащая в этом множестве
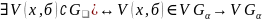
2)пусть
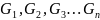 -открытое
множество и точка
-открытое
множество и точка
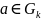 (каждому
открытому множеству).
(каждому
открытому множеству).
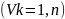 ,
значит
,
значит
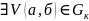 существует в точке обозн.через б=min
из
существует в точке обозн.через б=min
из
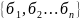 ,
тогда
,
тогда
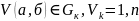 откуда ↔,что она будет содержать
откуда ↔,что она будет содержать
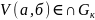 -
открытое множество.
-
открытое множество.
ОПР.
Множество
называется замкнутым, если
без х открыто, точка
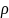 из
называется предельной точкой из мн. Х,
если
окрестность точки
соед. точки мн-ва х отличного от
.
из
называется предельной точкой из мн. Х,
если
окрестность точки
соед. точки мн-ва х отличного от
.
ОПР. Мн-ва Х замкнуто, тогда и только тогда, когда оно содержит все свои предельные точки.
ОПР.
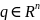 ,
наз. Точкой прикосновения множеств х,
если
окрестность этой точки содержит хотябы
одну точку мн-в х.
,
наз. Точкой прикосновения множеств х,
если
окрестность этой точки содержит хотябы
одну точку мн-в х.
ОПР.
Точка
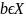 ,
наз. Изолированной точкой мн-в х, если
сущ. б-окрестность в точке b,
не содержит точек b
множ. Х кроме b.
,
наз. Изолированной точкой мн-в х, если
сущ. б-окрестность в точке b,
не содержит точек b
множ. Х кроме b.
ОПР. Объединим множество х и все его предельных точек наз. Замыкающим мн-ва х.
ОПР.множества
Х наз. Ограниченным, если сущ. шар
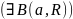 такой, что
такой, что
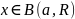 .
.
ОПР. Ограниченное, замкнутое множество это компакт.
ОПР. Непрерывное отображение отрезка [a,b] в пространстве наз. Путем.
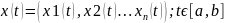 ;
2
пути
;
2
пути
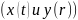 наз. эквивалентными, если сущ. строго
монотонная непр. ф-ия
наз. эквивалентными, если сущ. строго
монотонная непр. ф-ия
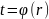 ,
отобр-я отрезок
,
отобр-я отрезок
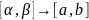 ;
;
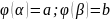 ;
множество всех эквивалентных путей
называется кривой.
;
множество всех эквивалентных путей
называется кривой.
