10 Ряды Фурье

Разложению в ряд Фурье могут подвергаться периодические сигналы. При этом они представляются в виде суммы гармонических функций либо комплексных экспонент с частотами, образующими арифметическую прогрессию. Для того чтобы такое разложение существовало, фрагмент сигнала длительностью в один период должен удовлетворять условиям Дирихле:

• не должно быть разрывов второго рода (с уходящими в бесконечность ветвями функции);

• число разрывов первого рода (скачков) должно быть конечным;

• число экстремумов должно быть конечным (sin(1/x) - пример функции, которая на конечном интервале имеет бесконечное число экстремумов в окрестности нуля).

В зависимости от конкретной формы базисных функций различают несколько форм записи ряда Фурье. Ряд Фурье может быть применен для представления не только периодических сигналов, но и сигналов конечной длительности. При этом оговаривается временной интервал, для которого строится ряд Фурье, а в остальные моменты времени сигнал считается равным нулю. Для расчета коэффициентов ряда такой подход фактически означает периодическое продолжение сигнала за границами рассматриваемого интервала.

С инусно-косинусная форма

ω — круговая частота, соответствующая периоду повторения сигнала, равному Т. Входящие в формулу кратные ей частоты kω, называются гармониками; гармоники нумеруются в соответствии с индексом k; частота ωk =kω, называется k-й гармоникой сигнала. Коэффициенты ряда ak и bk рассчитываются по формулам: Коэффициенты ряда ak и bk рассчитываются по формулам:

К онстанта α0 рассчитывается по общей формуле для αk. Поэтому введена форма записи постоянного слагаемого с делением на 2. Само слагаемое представляет собой среднее значение сигнала на периоде:

Интегрирование может производиться по любому интервалу длиной T— результат от этого не изменится. Конкретные пределы выбираются из удобства вычислений; например, может бытьинтегрирование от 0 до T или от -T до 0. Если s(t) является четной функцией, то все bk будут равны нулю и в формуле ряда Фурье будут присутствовать только косинусные слагаемые. Если s(t) является нечетной функцией, равны нулю будут, наоборот, косинусные коэффициенты ак и в формуле останутся лишь синусные слагаемые.

В ещественная форма Неудобство синусно-косинусной формы ряда Фурье - для каждого значения индекса суммирования k (то есть для каждой гармоники с частотой kω) в формуле два слагаемых — синус и косинус. По формулами тригонометрических преобразований можно получить косинус той же частоты с иной амплитудой и некоторой начальной фазой:

Если s(t) является четной функцией, фазы φk могут быть только 0 и p, а если s(t) — функция нечетная, то возможные значения для фазы равны ±p/2.

К омплексная формаДанная форма представления ряда Фурье является наиболее употребимой в радиотехнике. Она получается из вещественной формы представлением косинуса в виде полусуммы комплексных экспонент (такое представление вытекает из формулы Эйлера еxp(jx)= cos х + j sin x):

П рименив данное преобразование к вещественной форме ряда Фурье, получим суммы комплексных экспонент с положительными и отрицательными показателями:

Будем трактовать экспоненты со знаком «минус» в показателе как члены ряда с отрицательными номерами, постоянное слагаемое а0/2 станет членом ряда с нулевым номером. В результате получаем комплексную форму записи ряда Фурье:

К омплексная форма записи ряда Фурье: (**)

К омплексные коэффициенты ряда связаны с амплитудами Ак и фазами φk в вещественной форме записи ряда Фурье:

Формулы связи с коэффициентами ак и bк синусно-косинусной формы ряда Фурье:

Ф ормула непосредственного расчета коэффициентов Ск ряда Фурье в комплексной форме:

(*)

Если s(t) является четной функцией, коэффициенты ряда Ck будут чисто вещественными, а если s(t) — функция нечетная, коэффициенты ряда окажутся чисто мнимыми.

Совокупность амплитуд гармоник ряда Фурье часто называют амплитудным спектром, а совокупность их фаз — фазовым спектром. Не следует путать с АЧХ и ФЧХ, которые относятся не к сигналам, а к цепям.

11. Преобразование Фурье является инструментом спектрального анализа непериодических сигналов.

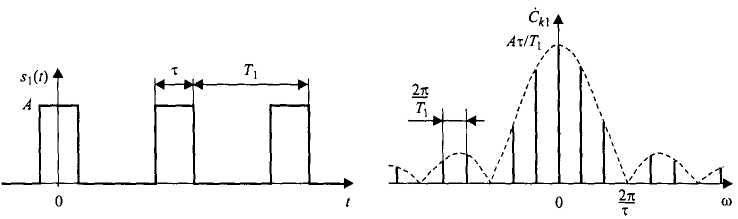Рис. Изменение спектра последовательности импульсов при двукратном увеличении периода их следования

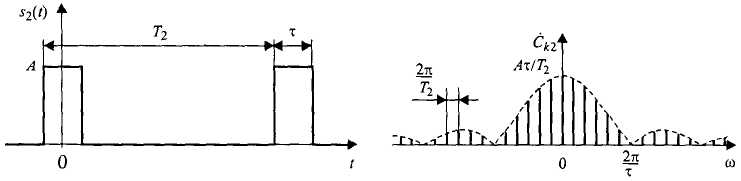
C ростом периода следования импульсов гармоники располагаются ближе друг к другу по частоте, а общий уровень спектральных составляющих становится все меньше.

(*)

Если устремить период к бесконечности (превратив тем самым

периодическую последовательность в одиночный импульс), гармоники спектра будут плотно занимать всю частотную ось, а их амплитуды упадут до нуля (станут бесконечно малыми). Однако взаимное соотношение между уровнями гармоник остается неизменным и определяется (*)

При спектральном анализе непериодических сигналов:

- частота перестает быть дискретно меняющейся и становится непрерывным параметром преобразования (то есть kω в формуле (*) заменяется на ω);

- удаляется множитель 1/T;

- результатом вычислений вместо нумерованных коэффициентов ряда Сk является функция частоты S(ω) — спектральная функция сигнала s(t). Иногда ее называют также спектральной плотностью.

Формула прямого преобразования Фурье:

Обратное преобразование Фурье:

Для применимости ПФ сигнал должен удовлетворять:

• у 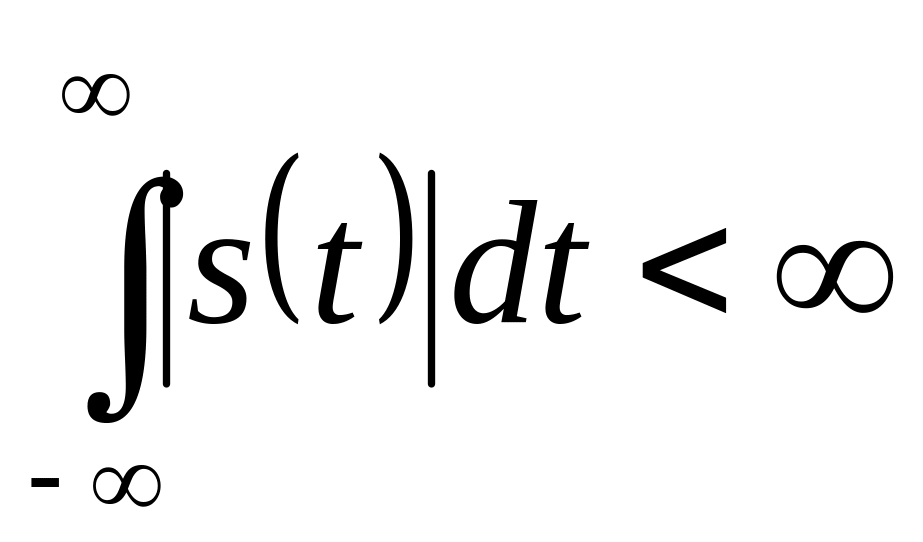словиям Дирихле

• быть абсолютно интегрируемым

В озможно выполнение Фурье-анализа и для некоторых сигналов, не удовлетворяющих этим требованиям. При преобразовании сигнала в пространство гармонических частот и обратно формулы прямого и обратного преобразований Фурье тождественны за исключением знака аргументов экспоненты

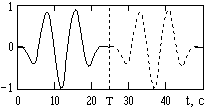
Сплошная кривая - пример непрерывного сигнала s(t), энергия которого сосредоточена на конечном интервале T = (0,25). Если форма данного сигнала за пределами интервала Т не важна, то спектр сигнала в виде ряда Фурье можно определить по формуле (*). При обратном преобразовании Фурье по формуле (**), т.е. при восстановлении сигнала по его спектру, в интервале Т будет восстановлен исходный сигнал s(t).

Если интервал для восстановления будет задан больше интервала Т, например равным 0-2Т, то за пределами этого интервала начнется периодическое повторение исходного сигнала, как это показано пунктиром. Если такой процесс нежелателен и за пределами интервала Т должны быть сохранены нулевые значения сигнала, то необходимо использовать интегральное преобразование Фурье.

Е сли s(t) – вещественная функция, то соответствующая спектральная функция S(ω) является «сопряженно-симметричной» относительно нулевой частоты, значения на частотах ω и –ω являются комплексно-сопряженными:

Модуль спектральной функции называют амплитудным спектром, а её аргумент – фазовым спектром. Для вещественного сигнала амплитудный спектр является четной, а фазовый – нечетной функцией частоты: Если s(t) – четная функция, то как и для ряда Фурье, спектр будет чисто вещественным (будет четной функцией).

Е сли s(t) – нечетная функция, то спектральная функция будет чисто мнимой и нечетной.

Преобразование Фурье ставит в соответствие сигналу, заданному во времени, его спектральную функцию. Осуществляется переход из временной области в частотную. Преобразование Фурье является взаимно-однозначным, поэтому представление сигнала в частотной области (спектральная функция) содержит ровно столько же информации, сколько исходный сигнал, заданный во временной области.

Свойства преобразования Фурье

Л инейность Преобразование Фурье является линейным интегральным преобразованием: спектр суммы равен сумме спектров.

З адержка Как сказывается на спектральной функции задержка сигнала по времени? Пусть t — время задержки:

- амплитудный спектр сигнала не меняется

- фазовый спектр имеет дополнительное слагаемое

Е сли в результате какого-либо преобразования сигнала его спектр умножается на некоторую функцию, не зависящую от преобразуемого сигнала, это означает, что данное преобразование может быть выполнено линейной системой с постоянными параметрами:

И зменение масштаба оси времени Общее практическое правило: чем короче сигнал, тем шире его спектр. Если изменить длительность сигнала f(t), сохраняя его форму, то новый сигнал s(t) следует записать как При |α|>1сигнал сжимается, при |α|<1— растягивается. Если α<0, дополнительно происходит зеркальное отражение сигнала относительно вертикальной оси. Такое преобразование сказывается и на спектре:

Изменение длительности сигнала приводит к

- изменению ширины спектра в противоположную сторону: аргумент t на α умножается, а на ω делится;

- увеличению (при растяжении α<1 ) или уменьшению (при сжатии α>1 ) уровня спектральных составляющих.

Полученная формула справедлива для α>0. При α<0 замена переменной t→α·t вызовет перестановку пределов интегрирования и, как следствие, изменение знака у результата:

Объединяя оба случая, можно записать

При α=-1 полученная формула дает: