1.2. Смешанные стратегии и теорема фон Неймана-Нэша

Ответ на вопрос, поставленный в предыдущем пункте, может быть получен благодаря применению «смешанных» стратегий.

Рассмотрим последовательность игр, в каждой из которых 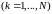игроки выбирают свои чистые стратегии и, соответственно, получают выигрыши 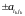Средний выигрыш первого игрока при этом

равен

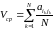
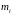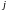Пусть − число игр, когда первый игрок выбрал свою -тую стратегию, − число игр, когда второй игрок выбрал свою -тую стратегию, причем ,

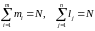где т − число чистых стратегий первого игрока, a n − второго. Очевидно, что некоторые или могут быть равны нулю (если соответствующие стратегии не выбирались ни разу).

Тогда − относительные частоты выбора стратегий, 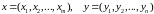− векторы частот.

.

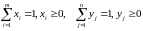Теорема фон Неймана-Нэша

Для любой матричной игры минимакс равен максимину, или − существуют 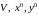, удовлетворяющие условиям:

.

1.3. Метод решения игры

Рассмотрим игру , т. е. когда у каждого из игроков имеются всего две стратегии (i = 1, 2; j = 1, 2).

Поскольку при равенстве нижних и верхних цен игры в чистых стратегиях решение очевидно (оно определяется седловой точкой матрицы), интерес представляет ситуация их неравенства. Но из теоремы Неймана-Нэша следует, что существует пара смешанных стратегий 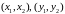, обеспечивающая равенство верхней и нижней цены игры (минимакса и максимина). Раз это не реализуется чистыми стратегиями, значит, цена игры V достигается при смешивании каждым игроком обеих своих стратегий (обе стратегии «активны») и при каждой чистой стратегии противника (иначе никакое смешивание не может улучшить результат), поэтому если

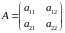, то 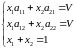(1.3.1)

Имеем три уравнения с тремя неизвестными. Вычитая из первого уравнения второе, получаем отношение

(1.3.2)

Знак абсолютной величины поставлен потому, что это отношение всегда положительно, так как при разных знаках у 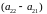и 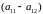одна из стратегий второго игрока явно хуже другой и не может им применяться.

Решение отношения (1.3.2) сводится к делению единичного отрезка на части, находящиеся в отношении

,

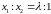
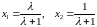после чего найти не представляет труда.

4. Приведение матричной игры к задаче линейного программирования

Решение игры может быть сведено к решению задачи линейного программирования.

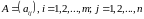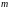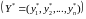Пусть игра задана платежной матрицей . Первый игрок обладает , второй − стратегиями. Необходимо определить оптимальные стратегии первого и второго игрока, где 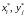− оптимальные частоты применения своих стратегий соответственно первым и вторым игроком.

.

Оптимальная стратегия X* обеспечивает первому игроку средний выигрыш, не меньший, чем цена игры V, при любой стратегии второго игрока и выигрыш, равный цене игры V, при оптимальной стратегии второго игрока.

Если первый игрок применяет смешанную стратегию X^* против любой чистой стратегии второго игрока, то он получает средний выигрыш, или математическое ожидание выигрыша V(j)=a_1jx₁+…a_mjx_m, j= 1, 2,…, п (т. е. элементы j-гo столбца платежной матрицы почленно умножаются на соответствующие вероятности стратегий первого игрока и результаты складываются).

Для оптимальной стратегии X^* все средние выигрыши не меньше цены игры V, поэтому получаем систему неравенств:

a₁₁x₁+a₂₁x₂+…+a_m1x_m V,

a₁₂x₁+a₂₂x₂+…+a_m2x_m V,

…………………….. (1.4.1)

a_1n x₁+a_2n x₂+…+a_mn x_m V.

Каждое из неравенств можно разделить на число V > 0. Введем новые переменные

z_i=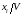 . (1.4.2)

Тогда система (1.4.1) примет вид:

(1.4.3)

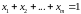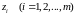Цель первого игрока — максимизировать свой гарантированный выигрыш, т. е. цену игры V. Разделив на равенство , получаем, что переменные удовлетворяют условию: .

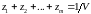Максимизация цены игры V эквивалентна минимизации величины 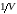, поэтому задача может быть сформулирована следующим образом: определить значения переменных 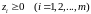так, чтобы они удовлетворяли линейным ограничениям (1.4.3) и при этом линейная функция

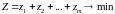(1.4.4)

обращалась в минимум. Это задача линейного программирования. Решая задачу (1.4.3) − (1.4.4), получаем оптимальные стратегии .

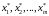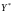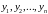Для определения оптимальной стратегии второго игрока следует учесть, что он стремится минимизировать гарантированный выигрыш первого игрока, т. е. найти . Переменные удовлетворяют неравенствам

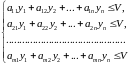(1.4.5)

которые следуют из того, что средний проигрыш второго игрока не превосходит цены игры, какую бы чистую стратегию не применял первый игрок.

Если обозначить

(1.4.6)

то получим систему неравенств:

(1.4.7)

Переменные 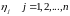, удовлетворяют условию .

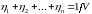Игра свелась к следующей задаче: определить значения переменных , которые удовлетворяют системе неравенств (1.4.7) и максимизируют линейную функцию

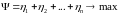(1.4.8)

Решение задачи линейного программирования (1.4.7) − (1.4.8) определяет оптимальную стратегию . При этом цена игры

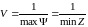. (1.4.9)

Задачи линейного программирования (1.4.3) − (1.4.4) и (1.4.7) − (1.4.8) являются взаимно двойственными. Очевидно, при определении оптимальных стратегий в конкретных задачах следует выбрать ту из взаимно двойственных задач, решение которой менее трудоемко, а решение другой задачи найти с помощью теорем двойственности.