ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ИНСТИТУТ ЭНЕРГЕТИКИ И МАШИНОСТРОЕНИЯ

Кафедра «Экономика и менеджмент в машиностроении»

Применение теории игр в экономических задачах

Методические указания к лабораторной работе

Ростов-на-Дону

2011

Составители:

кандидат физико-математических наук, доцент И. М. Пешхоев

кандидат экономических наук, доцент А.А. Алуханян

доцент Т.А. Иваночкина

УДК 336. 658

ПРИМЕНЕНИЕ ТЕОРИИ ИГР В ЭКОНОМИЧЕСКИХ ЗАДАЧАХ: Методические указания к лабораторной работе по дисциплине «Экономико-математическое моделированиет»/ДГТУ, Ростов н/Д, 2011. — 16 с.

Методические указания предназначены для студентов 3-го и 4-го курсов специальностей 080507 и 080502 всех форм обучения

Печатается по решению редакционно-издательского совета института энеогетики и машиностроения

Рецензент кандидат технических наук, доцент В. П. Гаценко

Научный редактор доктор экономических наук, профессор

М. В. Альгина

© Издательский центр ДГТУ, 2011.

Оглавление

1. Теоретические сведения ……………………………...4

1. Основные понятия теории матричных игр ……………………………..4

2. Смешанные стратегии и теорема фон Неймана-Нэша………………………..7

3. Метод решения игры 2 2………………………….……………………………8

4. Приведение матричной игры к задаче линейного программирования ……..11

2. Пример выполнения задания ……………………………..15

3. Задание к лабораторной работе ……………………………. 25

Литература ……………………………….27

1. Теоретические сведения

1.1. Основные понятия теории матричных игр

На практике часто приходится сталкиваться с задачами, в которых необходимо принимать решения в условиях неопределенности, т. е. возникают ситуации, в которых две (или более) стороны преследуют различные цели, а результаты любого действия каждой из сторон зависят от мероприятий партнера.

В экономике конфликтные ситуации встречаются очень часто и имеют многообразный характер. К ним относятся, например, взаимоотношения между

поставщиком и потребителем, покупателем и продавцом, банком и клиентом. Во всех этих примерах конфликтная ситуация порождается различием интересов партнеров и стремлением каждого из них принимать оптимальные решения, которые реализуют поставленные цели в наибольшей степени. При этом каждому приходится считаться не только со своими целями, но и с целями партнера, и учитывать неизвестные заранее решения, которые эти партнеры будут принимать.

Для решения задач с конфликтными ситуациями разработаны математической теорией конфликтных ситуаций, которая носит название теория игр.

Приведем основные понятия теории игр. Математическая модель конфликтной ситуации называется игрой, стороны, участвующие в конфликте − игроками, а исход конфликта − выигрышем. Для каждой формализованной игры вводятся правила, т. е. система условий, определяющая: 1) варианты действий игроков; 2) объем информации каждого игрока о поведении партнеров; 3) выигрыш, к которому приводит каждая совокупность действий. Как правило, выигрыш (или проигрыш) может быть задан количественно.

Игра называется парной, если в ней участвуют два игрока, и множественной, если число игроков больше двух. Рассматривать будем только парные игры. В них участвуют два игрока А и В, интересы которых противоположны, а под игрой будем понимать ряд действий со стороны А и В.

Игра называется игрой с нулевой суммой, или антагонистической, если выигрыш одного из игроков равен проигрышу другого.

Выбор и осуществление предусмотренных правилами действий называется стратегией игрока.

Целью теории игр является определение оптимальной стратегии для каждого игрока. При выборе оптимальной стратегии естественно предполагать, что оба игрока ведут себя разумно с точки зрения своих интересов.

Рассмотрим парную конечную игру. Пусть игрок А располагает т стратегиями, которые обозначим А₁ , А₂ , ... , А_m . У игрока В имеется п стратегий, обозначим их В₁, В₂ ,… , В_n .

В этом случае игра имеет размерность 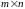. В результате выбора игроками любой пары стратегий

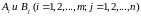
однозначно определяется исход игры, т. е. выигрыш 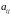игрока А (положительный или отрицательный) и проигрыш (- ) игрока В. Предположим, что значения известны для любой пары стратегий 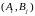. Матрица { }, (i=1,2,…, m; j = 1,2,…, п) элементами которой являются выигрыши, соответствующие стратегиям А_i и В_j , называется платежной матрицей. Строки этой матрицы соответствуют стратегиям игрока А, а столбцы − стратегиям игрока В.

Рассмотрим игру с матрицей { }, (i=1,2,…, m; j = 1,2,…, п) и

определим наилучшую среди стратегий А₁ , А₂ , ... , А_m . Выбирая стратегию А_i игрок А должен рассчитывать, что игрок В ответит на нее той из стратегий B_j, для которой выигрыш для игрока А минимален (игрок В стремится "навредить" игроку А).

Обозначим через 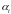, наименьший выигрыш игрока А при выборе им стратегии А_i для всех возможных стратегий игрока В (наименьшее число в 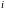-й строке платежной матрицы), т. е.

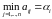(1.1.1)

Среди всех чисел 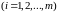выберем наибольшее: 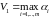. Назовем 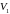нижней ценой игры или максиминным выигрышем (максимином). Это гарантированный выигрыш игрока А при любой стратегии игрока В. Следовательно,

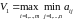, (1.1.2)

Стратегия, соответствующая максимину, называется максиминной стратегией. Игрок В заинтересован в том, чтобы уменьшить выигрыш игрока А; выбирая стратегию В_j он учитывает максимально возможный при этом выигрыш для А. Обозначим

(1.1.3)

Среди всех чисел 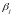выберем наименьшее 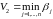и назовем 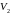верхней ценой игры или минимаксным выигрышем (мииимаксом). Это гарантированный проигрыш игрока В. Следовательно,

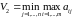(1.1.4)

Простые рассуждения позволяют понять, что всегда 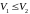. При 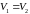гарантированный 1-му игроку выигрыш совпадает с тем выигрышем, выше которого второй игрок в состоянии не допустить выигрыша 1-го игрока, т. е. имеет место некоторое равновесие, которым игроки и должны удовлетвориться (при осторожной игре, без риска, так как отступление от этого поведения грозит возможным наказанием, уменьшением выигрыша или увеличением потерь). Эта ситуация отвечает наличию у платежной матрицы «седлового элемента» - максимального в столбце и минимального в строке.

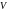В остальных случаях и возникает вопрос: нельзя ли увеличить гарантированный выигрыш и добиться того, чтобы выигрыш был между нижней и верхней ценой игры ?
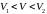