21. Колебания круглой мембраны. Понятие о функциях Бесселя.

.

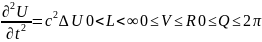
U(R,Q)=0-мембрана плоская

U(r,Q,0)=f(r,Q)-нач.смещение мембраны

Это линейное уравнение, однородное,т.е. колебания явл.свободными, с однородными граничными условиями.

U(r,Q,t)=U(r,Q)T(t)

UT’’=

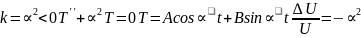
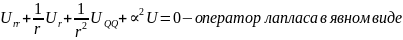
U(R,Q)=0граничные условия

U(r,Q)=R(r)Q(Q)

R’’(Q)+

rR’’Q+rR’Q+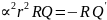

+…

После раскрытия скобок: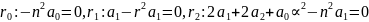

Ф-ция Бесселя 1ого рода порядка общее решение урав.имеет вид:

Рис.

Ф-ция Бесселя 2ого рода:

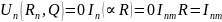
Общее решение:

решение в виде ряда функции Бесселя:

Acos

Нули ф-ции Бесселя расположены неравномерно, поэтому звук инструмента не музыкальный.

22.Численные методы. Метод конечных разностей для уравнения Лапласа.

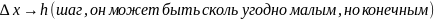
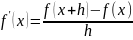- правая разностная произв. - левая разностная производная

Центральная разностная производная:

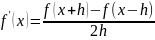- центр.разност.произ.

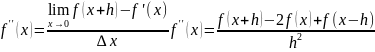
Шаг по одной переменной может быть неравен шагу по другой переменной

Задача: 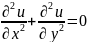0<X<1 0<Y<1 Граничные условия:

Рис.1

Вместо вычисления потенциала внутри квадрата мы сведем задачу к вычислению матрицы m*n

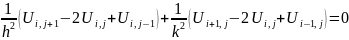
Разностный аналог уравнения Лапласа. Пусть h=k

m=n.Точкам внутри мы присваиваем значения на границе

Идея метода Лабмака:

1 шаг. Всем внутренним точкам присваиваем значения равные среднему значению на границе.

2 шаг. Начинаем пересчет по строкам или столбцам. При этом каждой точке матрицы присваиваем значение по формуле

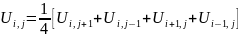
3 шаг. Повторяем шаг 2 пока не достигнем требуемой точки. где f- значение функции в данной точке.

23.Численные методы. Явные разностные схемы.Уравнение параболического типа

– уравнение теплопроводности для тонкого стержня

рис.1 Движение по сетке по времени

Мы заменим част.произв.на разностную(к= )

Пдставляем в ур-ие теплопроводности:

24. Численные методы. Неявные разностные схемы.

(1) (2)

Приравниваем 1=2 и находим , чему равно

Предельное значение ф-цииU=0:

(2*)

Приравниваем 1*=2*:

Введем параметр:

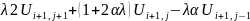
2 5. Численные методы. Метод Рунге-Кутта.

;

;

;

;

;

;

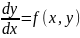
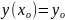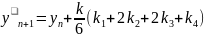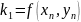Погрешность порядка h⁴.

26-27Применение метода Монте-Карло для вычисления определенных интегралов.

Идея: Кинули 100 камней причём равномерно. 36 камней – «плюх» - значит от а²(элемент. принцип Монте-Карло)

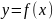
a,b=const

Предположим, что интегрлнеберущ. или, если берущ., то непонятный.

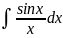- неберущ. интеграл

Кидали дротики. Часть попадает под интеграл, часть над интеграл. Сл-но сможем посчитать

Рис. Метод Монте-Карло хорош для многомерных интегралов. Например :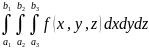

Метод Монте-Карло для решения уравнений эллиптического типа Рис. U/гр=g(x,y) 0<x<a0<y<b

Начало в точке А, и заканчивается в каждой точке на границе с поверхностью. При каждом шаге перебир. в одну из соседних точек с вер-тью ¼ . После многократного повторения, мы получаем относит. число прибытий в каждой из граничных точек. В каждой точке определяем вознаграждение (координаты точки). Точка А =>P_k – точка границы.

Найти ср. прогулок, начиная из точки А (R)

- вероятность того, что прибыв.в граничную точку – среднее вознаграждение, оно даёт нам приближ. Решение Лапласа.

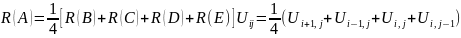
Этот метод:

1. Позволяет учесть несимметр. границу.

2. Удобен для многомерных интегралов

3. Нахождение значения функции на данной области и для определения точки в области.

лин. с переем.коэфф.

Подставляем в уравнение

=0

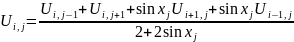
Сумм.коэфф. = 1

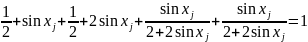
- взвешенное среднее значение в соседних точках.

Если раньше вероятность перехода в соседнюю точку = ¼ , то в данном случае одному из коэфф. ( ) (решили для линейных задач)