16. Течение грунтовых вод. Уравнение Буссинеска. Гидрологический барьер.

Уравнение Буссинеска описывает форму свободной поверхности жидкости при её течении в пористом грунте.

рис.11)жидкость считаем несжимаемой, плотность жидкости не зависит от t

2)пласт считаем тонким H+h<<размера пласта по горизонтали

3)H(x,y)-гладкая функция(т.е.непрерывная и имеет непрерывные производные)

4)давление на поверхность жидкости постоянное

5)грунт считаем однородным

Рис2 Элементарный объем:

H(x,y,t); V=(x,y,t);

Найдем, какое количество жидкости вытекает через элементарный объем:

1)В элементарном объеме накапливается:

2)в результате движения по у:

3)если пласт тонкий т смещение по оси z не происходит.; ᴂ-пористость грунта

найдем объем:

0<= ᴂ<=1ᴂ h)dydx-масса воды в элементе V

за время t произойдут изменения: h)dydx)dt= ( h)dydx)dt= dydxdt

dydxdt=-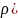 (V(H+h)dxdydt, ᴂ (V(H+h)

Дарси: U=- , ;

-если ур-иенеоднор.,то сист.замкнута.

еслиH>>h,H=const,не зависит от х,у,

Гидрологический барьер:

Риc3/

Что такое гидравлический барьер?

Гидравлический барьер образу­ется на границе раздела теплой воды с водой, имеющей температуру меньше температуры максимальной плотности. В зоне контакта холодная вода подогревается за счет смешивания с теплой, а теплая охлаждается. При температуре 4° С эта вода под действием гравитационных сил опускается на глубину и, как ширмой, ограничивает пространственное растекание и смешивание разнородных водных масс. Гидравлический барь­ер прослеживается на контакте тепловых вод притоков Байкала и холодных водных масс открытой части озера.

17,18. Приближенные аналитические решения. Метод теории возмущений для уравнения.Приближенные аналитические решения. Метод теории возмущений для границы.

0

,

>U(r,Q)=

,

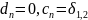
-символ Кронекера

U(r,Q)=rcosQ

Если ур-ие не лин.,граничные условия линейны

возмущ.уравнение

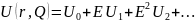
Подставим в уравнение:

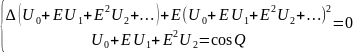
линейное неоднородное уравнение

ОРЛНУ=ОРОУ+УОНУ

Отбросим отриц.степени п, т.к.решение внутреннее

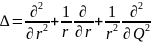
(r,Q)=

12 =>A=-1/32, B=-1/24

-1/32-1/24cosQ=0 =>

Общее решение:

Первое приближение:

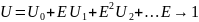
–аналитическое решение в первом приближен

19. Приближенные аналитические решения. Метод конформных отображений.

z=x+iy=

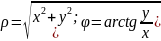; x=

Некое отображение:

W=f(z); w=U+iV

Отображение образуется в корд.х и у на некую поверхность.

Пример:

F(z)=

Рис.1 Отображение комплексной плоскости z на комплексную поверхность wназкомфорным в точке z0, если отображение наз.комфортным в области, если оно комфорно в каждой точке той области.

20. Приближенные аналитические решения. Использование степенных рядов.

Решаем уравнение в виде степенного ряда.

Y’=

Y’’=2

Это равенство выполняется при любых значениях х и это возможно только ,когда коэфф.прих=0

…

-рекурентное соотношение(каждый след.член выражается через предыдущий)

; ; ; ; ;

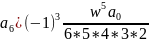Y=