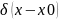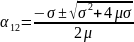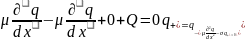- •Функционал. Вариация и её свойства.
- •2.Необходимое условие экстремума функционала. Уравнение Эйлера.
- •3) Функционалы вида: ;
- •4)Функционалы зависящие от производных порядка выше первого. Уравнение Эйлера-Пуассона.
- •5)Понятие об обобщённых функциях.
- •6.Дискретное логическое уравнение и его решения при различных значениях параметра.
- •7.Понятие о детерминированном хаосе. Странный аттрактор.
- •8.Задача Стефана о фазовом переходе. (рис)
- •9. Уравнение Римана. Ударные волны.
- •- Уравнение Римана.
- •10. Уравнение Кортевяга - де Фриза. Солитоны.
- •11.Фракталы. Фрактальная размерность.
- •12. Модель Мальтуса.
- •13. Модель Ферхюльста.
- •14. Модель «хищник-жертва».
- •15.Распределение примесей в атмосфере.
- •16. Течение грунтовых вод. Уравнение Буссинеска. Гидрологический барьер.
- •17,18. Приближенные аналитические решения. Метод теории возмущений для уравнения.Приближенные аналитические решения. Метод теории возмущений для границы.
- •19. Приближенные аналитические решения. Метод конформных отображений.
- •20. Приближенные аналитические решения. Использование степенных рядов.
- •21. Колебания круглой мембраны. Понятие о функциях Бесселя.
- •22.Численные методы. Метод конечных разностей для уравнения Лапласа.
- •23.Численные методы. Явные разностные схемы.Уравнение параболического типа
- •24. Численные методы. Неявные разностные схемы.
- •2 5. Численные методы. Метод Рунге-Кутта.
- •28.Приближенное решение уравнений в частных производных методами вариационного исчисления. Метод Ритца.
- •29.Принципы теории управления
- •30. Дифуры с запаздыванием.Модель хатчинсона
- •31. Матричная модель Лесли
- •32.Трофические функции.Метод линеаризации
- •33.Понятие о стохастическихдифурах
- •34. Функция Грина для круга
- •35. Понятие об ортогональных полиномах.
- •36. Ньютоновский потенциал.
- •Внешняя задача.
- •37. Уравнение Лапласа в сферических координатах.
- •38. Температурные волны в почве.
13. Модель Ферхюльста.
Это обобщённая модель Мальтуса. В этой модели вводится внутривидовая конкуренция.
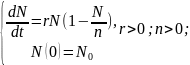 - уравнение
нелинейное.
- уравнение
нелинейное.
Тип
уравнения: уравнение Бернулли.
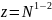 =
=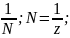
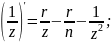
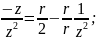
z’+rz=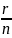 ;
- уравнение линейное, неоднородное.
;
- уравнение линейное, неоднородное.
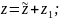

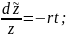
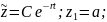
0+ra=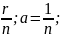
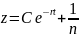 ;
⟹
;
⟹
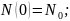
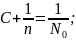
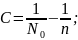
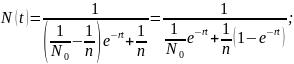
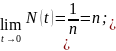
При
любом неч. условии предел будет =n.
(РИС. график по Мальтусу); к – в данном
случае – это ёмкость популяции т.е. то
количества особей, которые могут
прокормиться на данной территории.
N=const.
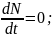 1)N=0;
2)N=k;
1)N=0;
2)N=k;
Если к->∞, то модель Ферхюльста принимает вид модели Мальтуса..
14. Модель «хищник-жертва».
(из нета для общего развития)
Допустим,
что на некоторой территории обитают
два вида животных:
кролики
(питающиеся растениями)
и лисы
(питающиеся кроликами). Пусть число
кроликов x,
число лис y.
Используя модель Мальтуса
с необходимыми поправками, учитывающими
поедание кроликов лисами, приходим к
следующей системе, носящей имя модели
Лотки — Вольтерра: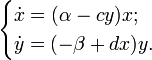
Эта система имеет равновесное состояние, когда число кроликов и лис постоянно. Отклонение от этого состояния приводит к колебаниям численности кроликов и лис, аналогичным колебаниям гармонического осциллятора. Как и в случае гармонического осциллятора, это поведение не является структурно устойчивым: малое изменение модели (например, учитывающее ограниченность ресурсов, необходимых кроликам) может привести к качественному изменению поведения. Например, равновесное состояние может стать устойчивым, и колебания численности будут затухать. Возможна и противоположная ситуация, когда любое малое отклонение от положения равновесия приведет к катастрофическим последствиям, вплоть до полного вымирания одного из видов.
В этой модели два вида взаимодействия. Аналитических решений нет, только численные.
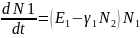
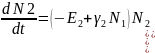 -простейшее квадратичное
уравнение
-простейшее квадратичное
уравнение
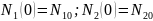 ;
Eи -положительные;
;
Eи -положительные;
 -коэфф.смертности
хищника в отсутствие жертвы
-коэфф.смертности
хищника в отсутствие жертвы
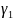 -характерн.скорость
потребления жертвы хищником
-характерн.скорость
потребления жертвы хищником
Характерный прирост биомассы хищника за счет биомассы жертвы
Рис.1 Рис.2
-1-ое решение тривиально
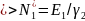 ;
;
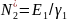 f(t+T)=f(t)<f>=
f(t+T)=f(t)<f>=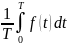 -среднее
значение за период
-среднее
значение за период

Проинтегрируем систему от 0 до Т:
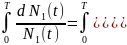
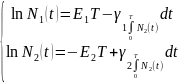
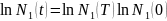
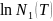 /
/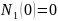
 <
<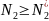 ;
<
;
<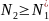
Вывели закон сохранения средних значений. Среднее значение численности каждого вида равно равновесному значению вида.
Введение управления фактора:
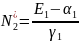 ,
,
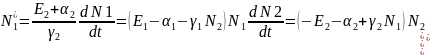
Варианты:1)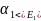 =>
=> ,
2)
,
2)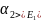 =>численность жертвы убывает, и убывает
численность хищников.
=>численность жертвы убывает, и убывает
численность хищников.
15.Распределение примесей в атмосфере.
q-концентрац.примесей
=>
 ,
,
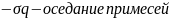 ,
,
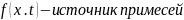 ; Q
; Q ,f(x,y,z)-распредюист.загрязнения,
Q(t)
Q
,f(x,y,z)-распредюист.загрязнения,
Q(t)
Q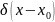 -источник
нах на одном месте, Q(t)
Q
-источник
нах на одном месте, Q(t)
Q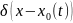 -источник
движется.
-источник
движется.
Рассм.упрощенную
задачу:
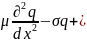 Q
=0
Q
=0
1)нет зависимости от времени,2)точечный источник примеси
Найти
распространение примеси по всей числовй
оси: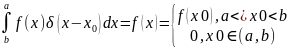
Проинтегрируем
урапвнение: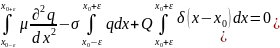
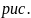 1
=>
1
=>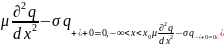
При

Хар.уравнение: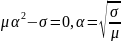
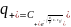 -на
конечных условиях примесь должна
-на
конечных условиях примесь должна
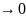

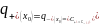 =C
=C

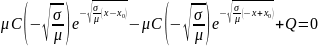
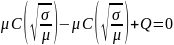
 ,
,
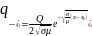
Рис.2
-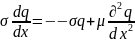 +Q
+Q