
- •Функционал. Вариация и её свойства.
- •2.Необходимое условие экстремума функционала. Уравнение Эйлера.
- •3) Функционалы вида: ;
- •4)Функционалы зависящие от производных порядка выше первого. Уравнение Эйлера-Пуассона.
- •5)Понятие об обобщённых функциях.
- •6.Дискретное логическое уравнение и его решения при различных значениях параметра.
- •7.Понятие о детерминированном хаосе. Странный аттрактор.
- •8.Задача Стефана о фазовом переходе. (рис)
- •9. Уравнение Римана. Ударные волны.
- •- Уравнение Римана.
- •10. Уравнение Кортевяга - де Фриза. Солитоны.
- •11.Фракталы. Фрактальная размерность.
- •12. Модель Мальтуса.
- •13. Модель Ферхюльста.
- •14. Модель «хищник-жертва».
- •15.Распределение примесей в атмосфере.
- •16. Течение грунтовых вод. Уравнение Буссинеска. Гидрологический барьер.
- •17,18. Приближенные аналитические решения. Метод теории возмущений для уравнения.Приближенные аналитические решения. Метод теории возмущений для границы.
- •19. Приближенные аналитические решения. Метод конформных отображений.
- •20. Приближенные аналитические решения. Использование степенных рядов.
- •21. Колебания круглой мембраны. Понятие о функциях Бесселя.
- •22.Численные методы. Метод конечных разностей для уравнения Лапласа.
- •23.Численные методы. Явные разностные схемы.Уравнение параболического типа
- •24. Численные методы. Неявные разностные схемы.
- •2 5. Численные методы. Метод Рунге-Кутта.
- •28.Приближенное решение уравнений в частных производных методами вариационного исчисления. Метод Ритца.
- •29.Принципы теории управления
- •30. Дифуры с запаздыванием.Модель хатчинсона
- •31. Матричная модель Лесли
- •32.Трофические функции.Метод линеаризации
- •33.Понятие о стохастическихдифурах
- •34. Функция Грина для круга
- •35. Понятие об ортогональных полиномах.
- •36. Ньютоновский потенциал.
- •Внешняя задача.
- •37. Уравнение Лапласа в сферических координатах.
- •38. Температурные волны в почве.
8.Задача Стефана о фазовом переходе. (рис)
Есть
полу бесконечный океан на берегу истоков
холодильные установки воспроизводящие
t=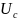 ˂0.
Выясним закон движения волны на берегу
океана. Скорость распространения:
˂0.
Выясним закон движения волны на берегу
океана. Скорость распространения:

 0<x<
0<x<




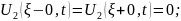
 - на границе
происходит скачок теплового потока.
- на границе
происходит скачок теплового потока.
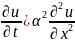 ;
;
α= ;
α=α(U);
;
α=α(U);

 α(u)=
α(u)=
Примеры преобразования Больцмана:
Замена
:
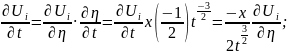


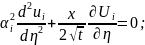

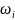 =
=
 - методом разделения
переменных.
- методом разделения
переменных.
 интегрируем.
интегрируем.
ln| ;
;
(
d ;
;
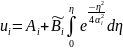 ;
;
Введём
новую функцию: erf(z)= (
(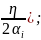
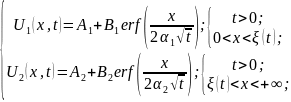
Граничные
условия:


На
границе:



(t)=β x=(t)=
β
x=(t)=
β
⟹
⟹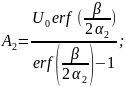
Выделение
тепла кристаллизации:
[ η
η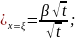
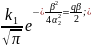
9. Уравнение Римана. Ударные волны.
Волны – это распространение частиц в пространстве.
 – уравнение
распространения волны. Где u
– плотность вещества, а q
– плотность потока. q=vu;
– уравнение
распространения волны. Где u
– плотность вещества, а q
– плотность потока. q=vu;
 d(x-vt)=0;
x-vt-c;
d(x-vt)=0;
x-vt-c;
U(x,t)=f(x-vt), U – любая дифференцированная функция.
𝛏=x-vt;
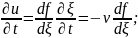

-v U(x,0)=ϕ(x-vt);
U(x,0)=ϕ(x-vt);
 q=du+b
q=du+b
 - нелинейное
уравнение.
- нелинейное
уравнение.
Замена:
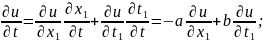
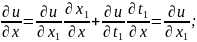
-a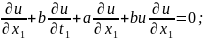
- Уравнение Римана.
 ;
;
Решение
уравнения Римана и будет некая функция
вида:
U(x,0)=f(x) (РИС а, б, в) Чем выше точка на волне, тем больше скорость. Верхние точки обгоняют нижние и волна запрокидывается.
Примеры: волна разбивается о берег.
Из уравнения мелкой волны:
 (РИС)
(РИС)Возможная ситуация когда происходит скачок плотности. (РИС)
 ;
;
 – уравнение
Бюргеса.
– уравнение
Бюргеса.
 ;
;
Диффузия сглаживает фронт волны, но не меняет её скорость.
10. Уравнение Кортевяга - де Фриза. Солитоны.
Солито́н — структурно устойчивая уединённая волна, распространяющаяся в нелинейной среде.Солитоны ведут себя подобно частицам (частицеподобная волна): при взаимодействии друг с другом или с некоторыми другими возмущениями они не разрушаются, а двигаются, сохраняя свою структуру неизменной. Это свойство может использоваться для передачи данных на большие расстояния без помех.
Солитоны бывают различной природы:
на поверхности жидкости (первые солитоны, обнаруженные в природе), иногда считают таковыми волны цунами и бор
ионозвуковые и магнитозвуковыесолитоны в плазме
гравитационные солитоны в слоистой жидкости
солитоны в виде коротких световых импульсов в активной среде лазера
предположительно, примером солитона является Гигантскийгексагон на Сатурне
можно рассматривать в виде солитонов нервные импульсы
Одной из простейших и наиболее известных моделей, допускающих существование солитонов в решении, является уравнение Кортевега — де Фриза:
Уравнение
дисперсии (линейной):
Кортевяг
де Фриз, уравнение:
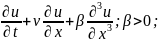 (
уравнение не линейное за счёт второго
слогаемого). Решение в виде: u=u(x-vt),
x-vt=𝛏;
v>0;
(
уравнение не линейное за счёт второго
слогаемого). Решение в виде: u=u(x-vt),
x-vt=𝛏;
v>0;




 =a
=a


3β
3β =F(u);
F(u)
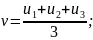 a=
a= ;
b=
;
b=
Предположим,
что все три корня вещественные: ;
F(u)>0;
;
F(u)>0;
 ;
(РИС) Предположим:
;
(РИС) Предположим:
Выберем начальные условия так, чтобы постоянные а и b дали бы такие решения:
3 =
=
 =u
=u ;
;

 =-
=-
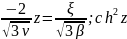 =
=
U(x,t)=3v );
);
 А – амплитуда.
А – амплитуда.
1≤ ;
0≤
;
0≤ ;
0≤u(x,t)≤A;
(РИС)
;
0≤u(x,t)≤A;
(РИС)
Чем выше солитон, тем больше его скорость;
Чем больше высота, тем меньше ширина;
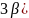 F(u)=
F(u)=
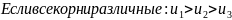 u(𝛏)=
u(𝛏)= ;
s=
;
s=
cn- эллиптический косинус. Уравнение Кортевяга да Фриза определяется множеством решений.
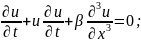
 s,t=const.
s,t=const.
Решение уравнения при такой замене будет многосолитонное. (РИС)
При взаимодействии 2х солитонов они получают дополнительное перемещение: быстрый – вперёд, а медленный – назад.
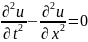 -
уравнение колебаний струны. Линейное,
однородное с 2мя переменными,
гиперболического типа.
-
уравнение колебаний струны. Линейное,
однородное с 2мя переменными,
гиперболического типа.
 - нелинейное
уравнение. Уравнение sin
Гордона.
- нелинейное
уравнение. Уравнение sin
Гордона.
