Функционал. Вариация и её свойства.
Функционал - это величина, значение которой определяется одной или несколько функций.
-
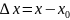приращение аргумента.
-
вариация аргумента функционала.
Функционал называется непрерывным, если малое изменение функции влечёт малое изменение функционала.
Вариационное исчисление изучает методы позволяющие находить мин. и мах значений функционала.
Вариационные принципы- задачи в которых, некий функционал должен достигнуть мин либо мах.
Линейный
функционал:L[
Вариация
функционала:
если
Вариация функционала- это дифференциал функции.
Функционал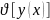
достигаетна
кривой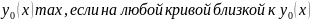
его
значение не больше чем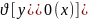
РИС.
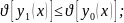
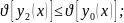
Для мин. тоже самое только знак >
Если функция достигает мин. во внутренней точке интеграла, дифференциал в этой точке равен нулю.
2.Необходимое условие экстремума функционала. Уравнение Эйлера.
-
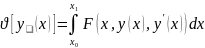уравнение Эйлера. F-
Некоторая функция 3х переменных. Это
задача с закреплёнными границами,
т.е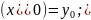y
y
.
:
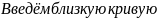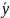и введём параметр α т.е.: y(x,α)=y(x)+α(
;
y(x,0)=y(x); если α=0
y(x,1)=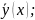
если α=1
Вариация
линейна, если вариация производной
равна производной вариации. (
=
);
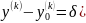Найдём функцию для которой функционал
имеет экстремум.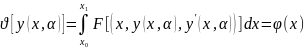
Мы предположим, что функционал имеет
экстремум на ф-и y(x),
т.е. при α=0;
ϕ’(0)=0;
1)ϕ(α)=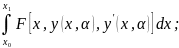
ϕ’(α)=
;
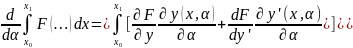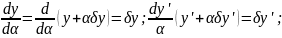ϕ’(α)=
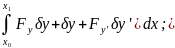Положим, что α=0
то получим: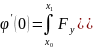
где ϕ’(0)-
экстремум ϕ’(0)=0;
б)
;
;
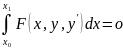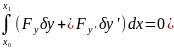Доказательство:
если интеграл =0, то это возможно тогда,
когда Ф(х)=0, ϵ[
Уравнение
эйлера:
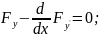если взять полную производную по
(x,y,y’):
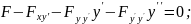Необходимое
условие нахождения экстремума – это
уравнение Эйлера.
Частные
случаи уравнения Эйлера: 1)F=F(x,y)
не зависит от y’.
уравнение Эйлера в этом случае не имеет
решений, но если ф-ция y
уд.условию:
;
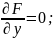
2)Линейная зависимость от y’: F(x,y,y’)=M(x,y)+N(x,y)y’; берём производную па у:
(Mdx+Ndy)
если полный дифференциал равен нулю,
то интеграл исходит из начальной точки.
3)если
значение ф-и зависит только от y’:
график- прямая.
4)
если функция зависит от x
и y’:
F=F(x,y’);
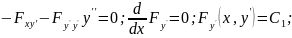
5)Функция
явно не зависит от х: F=F(y,y’);
F-y’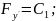
3) Функционалы вида: ;
jϵ[1,n]-любое
число из этой функции.
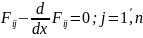– система дифференциальных уравнений
Эйлера.
Пример(1)
- граничные условия.
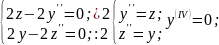
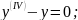
=0;
(
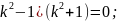
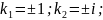
y=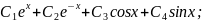
z=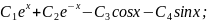
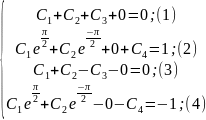
Из
сравнения (1) и (3)следует что
;а
из сравнения (2) и (4) ->
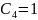
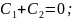
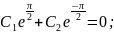
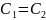=0;
y=sinx; z=-sinx;
Ответ:
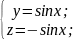
4)Функционалы зависящие от производных порядка выше первого. Уравнение Эйлера-Пуассона.
;
y(x)=y;
y(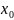
)=
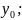
y(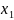
)=
…………
;
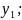
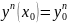y’(x)=y’;
;
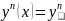Функция F – диффер. (n+2) раза по всем переменным.
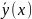– переменная,
которая проходит через х, но экстремума
на ней нет!!!.
y(x,α)=y(x)+α(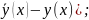
y(x,0)=y(x);
y(x,1)=
v=v(α) РИС!!!
Функционал v стал функцией параметра α: v=v(α) при α=0- достигнут экстремум.
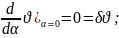
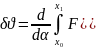(x,α))dx=
+
;
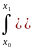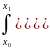
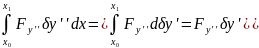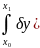
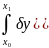]dx=0;
Уравнение
Эйлера –Пуассона:
=0;