3. Потенциальность электростатического поля. Интегральная и дифференциальная связь напряженности и потенциала.

Поле называется потенциальным, если работа при перемещении частицы на которую действует поле, по замкнутому полю равна нулю.

Согласно теореме о циркуляции вектора напряженности электростатического поля в вакууме работа сил электростатического поля при перемещении точечного заряда по любому контуру всегда равна нулю. Следовательно, поле является потенциальным.

.

  – теорема о циркуляции вектора Е           

Формула связи потенциала и напряженности:

4. Теорема Остроградского-Гаусса для электростатического поля в вакууме (без вывода) и применение теоремы к расчету поля заряженной плоскости и сферы.

Теорема Остроградского-Гаусса:

Поток вектора напряженности электростатического поля сквозь замкнутую поверхность равен отношению алгебраической суммы зарядов охваченных этой поверхностью к электрической постоянной.

• Поле заряженного тела должно быть симметрично

• Необходимо выбрать гауссову поверхность так, чтобы Е=const

Поверхностная плотность заряда на произвольной плоскости площадью S определяется по формуле: где dq – заряд, сосредоточенный на площади dS; dS – физически бесконечно малый участок поверхности.

Пусть σ во всех точках плоскости S одинакова. Заряд q – положительный. Напряженность   во всех точках будет иметь направление, перпендикулярное плоскости S (рис. 2.11).

Очевидно, что в симметричных, относительно плоскости точках, напряженность   будет одинакова по величине и противоположна по направлению.

Представим себе цилиндр с образующими, перпендикулярными плоскости, и основаниями ΔS, расположенными симметрично относительно плоскости (рис. 2.12).

Рис. 2.11

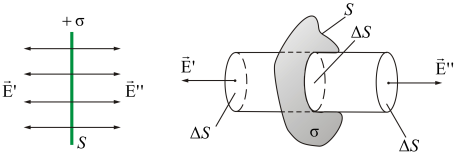Рис. 2.12

Тогда 

Применим теорему Остроградского-Гаусса. Поток Ф_Е через боковую часть поверхности цилиндра равен нулю, т.к.  Для основания цилиндра 

Суммарный поток через замкнутую поверхность (цилиндр) будет равен:

Внутри поверхности заключен заряд  . Следовательно, из теоремы Остроградского–Гаусса получим: , откуда видно, что напряженность поля плоскости S равна:

Полученный результат не зависит от длины цилиндра. Это значит, что на любом расстоянии от плоскости 

 Пустотелый шар (или сфера) радиуса R заряжен положительным зарядом с поверхностной плотностью σ. Поле в данном случае будет центрально симметричным – в любой точке проходит через центр шара. Силовые линии перпендикулярны поверхности в любой точке. Вообразим вокруг шара – сферу радиуса r (рис. 2.17).

Если  то внутрь воображаемой сферы попадет весь заряд q, распределенный по сфере, тогда: , откуда поле вне сферы:

Внутри сферы, при   поле будет равно нулю, т.к. там нет зарядов: 

       

Рис. 2.17

Как видно из (2.5.7) вне сферы поле тождественно полю точечного заряда той же величины, помещенному в центр сферы.