- •Электрический заряд. Электрическое поле. Основные характеристики электростатического поля – напряженность и потенциал. Графическое представление электростатических полей.
- •Напряженность и потенциал электростатического поля. Расчет полей методом суперпозиции (заряженный стержень, кольцо).
- •Потенциальность электростатического поля. Интегральная и дифференциальная связь напряженности и потенциала.
- •Теорема Остроградского-Гаусса для электростатического поля в вакууме (без вывода) и применение теоремы к расчету поля заряженной плоскости и сферы.
- •Электростатическое поле в диэлектриках. Диполи. Поведение диполя в однородном и неоднородном электростатическом поле. Поляризованность (вектор поляризации).
- •Теорема Остроградского-Гаусса для электростатического поля в диэлектрике (вывод). Вектор электрического смещения, диэлектрическая проницаемость и диэлектрическая восприимчивость.
- •Поведение двух векторов e & d на границе двух диэлектриков.
- •Теорема Остроградского-Гаусса для электростатического поля в диэлектрике (без вывода). Свободные и связанные заряды. Расчет поля диэлектрика в виде цилиндра с равномерно распределенным зарядом.
- •Проводники в электростатическом поле. Емкость. Конденсаторы.
- •Емкость. Конденсаторы. Энергия электростатического поля.
- •Постоянный электрический ток. Вектор плотности тока. Классическая теория электропроводимости металлов. Закон Ома в дифференциальной форме.
- •Закон Ома в интегральной форме. Обобщенный закон Ома.
- •Магнитное поле. Вектор магнитной индукции, как силовая характеристика магнитного поля. Силовые линии магнитного поля.
- •Магнитное поле тока. Закон Био-Савара-Лапласа и его применение к расчету магнитной индукции на оси кругового витка с током методом суперпозиции.
- •Расчет магнитного поля прямолинейного проводника с током с помощью закона Био-Савара-Лапласа и принципа суперпозиции.
- •Закон полного тока для магнитного поля в вакууме. Сцепленный ток. Применение закона полного тока для расчета магнитного поля тороида.
- •Применение закона полного тока для расчета магнитного поля тока тороида и длинного соленоида. Вихревой характер магнитного поля.
- •Силовое действие магнитного поля на проводник с током и контур с током.
- •Движение заряженных частиц в магнитном поле. Сила Ампера и Лоренса.
- •Магнитный поток. Теорема Гаусса для магнитного поля. Работа по перемещению проводника и контура с током в магнитном поле.
- •Явление электромагнитной индукции. Законы Фарадея-Максвелла. Правило Ленца. Вывод закона электромагнитной индукции на основе электронной теории.
- •Явление самоиндукции. Токи замыкания и размыкания. Взаимная индукция.
- •Энергия магнитного поля. Объемная плотность энергии.
- •Магнитное поле в веществе. Магнитные моменты атомов. Намагниченность. Макро- и микротоки.
- •Закон полного тока для магнитного поля в веществе. Напряженность магнитного поля. Поведение векторов в и н на границе магнетиков.
- •Типы магнетиков. Магнитная проницаемость. Элементарная теория диа- и парамагнетизма.
- •Ферромагнетики. Домены. Гистерезис. Точка Кюри.
- •Основы теории Максвелла для электромагнитного поля. Уравнения Максвелла в интегральной форме. Ток смещения.
- •Гармонические электромагнитные колебания и их характеристики. Электрический колебательный контур. Дифференциальное уравнение собственных гармонических колебаний и его решение.
- •Затухающие электромагнитные колебания. Дифференциальное уравнение и его решение. Логарифмический декремент.
- •Вынужденные электромагнитные колебания. Амплитуда и фаза вынужденных колебаний. Резонанс.
- •Сложение однонаправленных и взаимно перпендикулярных колебаний.
Вынужденные электромагнитные колебания. Амплитуда и фаза вынужденных колебаний. Резонанс.
Вынужденными
электромагнитными колебаниями называют
периодические изменения силы тока и
напряжения в электрической цепи,
происходящие под действием переменной
синусоидальной ЭДС от внешнего источника
![]() .
.
Синусоидальная ЭДС возникает при
вращении рамки с угловой скоростью ω в
стационарном магнитном поле с индукцией B.
Согласно закону электромагнитной
индукции

![]() (1).
(1).
Из формулы (1) следует,
что амплитуда А смещения (заряда) имеет
максимум. Чтобы определить резонансную
частоту ωrez ,
— частоту, при которой амплитуда А
смещения (заряда) будет максимальна, —
нужно найти максимум функции (1) или
минимум подкоренного выражения.
Продифференцировав выражение под корнем
по ω и приравняв его нулю, получим
условие, из которого найдем ωrez : ![]() Явление
резкого возрастания амплитуды вынужденных
колебаний при приближении частоты
вынуждающей силы (частоты вынуждающего
переменного напряжения) к частоте,
равной или близкой собственной частоте
колебательной системы, называется
резонансом.
Явление
резкого возрастания амплитуды вынужденных
колебаний при приближении частоты
вынуждающей силы (частоты вынуждающего
переменного напряжения) к частоте,
равной или близкой собственной частоте
колебательной системы, называется
резонансом.
Это
равенство верно при ![]() ,
у которых только выражение со знаком
плюс имеет физический смысл. Значит,
резонансная частота
,
у которых только выражение со знаком
плюс имеет физический смысл. Значит,
резонансная частота
![]() (2)
При
ω02 >>
δ2 значение
ωrez практически
равно собственной частотой ω0 колебательной
системы. Подставляя (2) в формулу (1)
предыдущего раздела, найдем
(2)
При
ω02 >>
δ2 значение
ωrez практически
равно собственной частотой ω0 колебательной
системы. Подставляя (2) в формулу (1)
предыдущего раздела, найдем
![]() (3)
(3)
Из
формулы (3) следует, что при малом затухании
(ω02 >>
δ2)
резонансная амплитуда смещения
(заряда)
![]() ,
где Q — добротность
колебательной системы, x0/ω02 -
статическое отклонение. Значит,
добротность Q характеризует резонансные
свойства колебательной системы: чем
больше Q, тем больше Аrez.
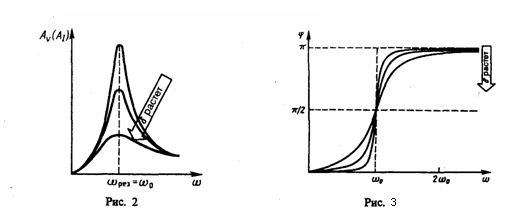
На
рис. 2 даны резонансные кривые для
амплитуды скорости (тока). Амплитуда
скорости (тока)
,
где Q — добротность
колебательной системы, x0/ω02 -
статическое отклонение. Значит,
добротность Q характеризует резонансные
свойства колебательной системы: чем
больше Q, тем больше Аrez.
На
рис. 2 даны резонансные кривые для
амплитуды скорости (тока). Амплитуда
скорости (тока)
![]() достигает
максимального значения при ωrez=ω0 и
равна x0/(2δ)
, т. е. чем больше коэффициент затухания
δ , тем ниже максимум резонансной кривой.
Применяя выражения для циклического
частоты свободных колебаний пружинного
маятника, формулы δ=r/(2m) и и выражение
для циклической частоты свободно
колеблющегося колебательного контура
вместе с δ=r/(2m), получим, что амплитуда
скорости при механическом резонансе
равна
достигает
максимального значения при ωrez=ω0 и
равна x0/(2δ)
, т. е. чем больше коэффициент затухания
δ , тем ниже максимум резонансной кривой.
Применяя выражения для циклического
частоты свободных колебаний пружинного
маятника, формулы δ=r/(2m) и и выражение
для циклической частоты свободно
колеблющегося колебательного контура
вместе с δ=r/(2m), получим, что амплитуда
скорости при механическом резонансе
равна
![]() а
амплитуда тока при электрическом
резонансе будет
а
амплитуда тока при электрическом
резонансе будет
![]() Из
выражения tgφ = 2δω/(ω02 -
ω2)
вытекает, что если в системе отсутствует
затухание (δ=0), то только в этом случае
колебания и вынуждающая сила (приложенное
переменное напряжение) имеют одинаковые
фазы; во всех других случаях
φ≠0.
Зависимость
φ от ω при разных значениях δ графически
изображена на рис. 3, из которого вытекает,
что при изменении ω изменяется и сдвиг
фаз φ. Из формулы (9) предыдущего раздела
следует, что при ω=0 φ=0, а при ω=ω0 независимо
от значения коэффициента затухания φ
= π/2, т. е. сила (напряжение) опережает по
фазе колебания на π/2. При дальнейшем
росте ω сдвиг фаз возрастает и при
ω>>ω0 ,
т. е. φ→π фаза колебаний почти противоположна
фазе внешней силы (переменного напряжения).
Множество кривых, изображенных на рис.
3, называется фазовыми
резонансными кривыми.
Явления
резонанса могут быть как полезными, так
и вредными. Например, при конструировании
машин и различного рода сооружений
нужно, чтобы собственная частота
колебаний их не совпадала с частотой
возможных внешних воздействий, в
противном случае возникнут вибрации,
которые могут вызвать серьезные
повреждения. С другой стороны, наличие
резонанса дает возможность обнаружить
даже очень слабые колебания, если их
частота совпадает с частотой собственных
колебаний прибора. Так, прикладная
акустика, радиотехника, электротехника
используют явление резонанса.
Из
выражения tgφ = 2δω/(ω02 -
ω2)
вытекает, что если в системе отсутствует
затухание (δ=0), то только в этом случае
колебания и вынуждающая сила (приложенное
переменное напряжение) имеют одинаковые
фазы; во всех других случаях
φ≠0.
Зависимость
φ от ω при разных значениях δ графически
изображена на рис. 3, из которого вытекает,
что при изменении ω изменяется и сдвиг
фаз φ. Из формулы (9) предыдущего раздела
следует, что при ω=0 φ=0, а при ω=ω0 независимо
от значения коэффициента затухания φ
= π/2, т. е. сила (напряжение) опережает по
фазе колебания на π/2. При дальнейшем
росте ω сдвиг фаз возрастает и при
ω>>ω0 ,
т. е. φ→π фаза колебаний почти противоположна
фазе внешней силы (переменного напряжения).
Множество кривых, изображенных на рис.
3, называется фазовыми
резонансными кривыми.
Явления
резонанса могут быть как полезными, так
и вредными. Например, при конструировании
машин и различного рода сооружений
нужно, чтобы собственная частота
колебаний их не совпадала с частотой
возможных внешних воздействий, в
противном случае возникнут вибрации,
которые могут вызвать серьезные
повреждения. С другой стороны, наличие
резонанса дает возможность обнаружить
даже очень слабые колебания, если их
частота совпадает с частотой собственных
колебаний прибора. Так, прикладная
акустика, радиотехника, электротехника
используют явление резонанса.