23. Энергия магнитного поля. Объемная плотность энергии.

Магнитное поле обладает энергией. Подобно тому, как в заряженном конденсаторе имеется запас электрической энергии, в катушке, по виткам которой протекает ток, имеется запас магнитной энергии. 

Из закона сохранения энергии следует, что вся энергия, запасенная в катушке, выделится в виде джоулева тепла. Если обозначить через R полное сопротивление цепи, то за время Δt выделится количество теплоты ΔQ = I² R Δt.

Ток в цепи равен  

Выражение для ΔQ можно записать в виде 

ΔQ = –L I ΔI = –Φ (I) ΔI.

В этом выражении ΔI < 0; ток в цепи постепенно убывает от первоначального значения I₀ до нуля. Полное количество теплоты, выделившейся в цепи, можно получить, выполнив операцию интегрирования в пределах от I₀ до 0. Это дает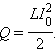 

Энергия магнитного поля, создаваемого током в замкнутом контуре индуктивностью L, равна  где I — сила тока в контуре.

Энергия магнитного поля катушки с индуктивностью L, создаваемого током I, равна

Энергию магнитного поля можно рассматривать как функцию величин, которые характеризуют это поле в окружающем пространстве. Для этого рассмотрим частный случай — однородное магнитное поле внутри длинного соленоида. Подставив в формулу энергии формулу индуктивности соленоида, найдем  .  Так как I=Bl/(μ₀μN) и В=μ₀μH , то   (2). Магнитное поле внутри соленоида однородно и сосредоточено внутри него, поэтому энергия (2) заключена в объеме соленоида и имеет с нем однородное распределение с постоянной объемной плотностью  . Эта формула выводилась для однородного поля, но она верна и для неоднородных полей, также она справедлива только для сред, для которых  зависимость В от Н линейная, т.е. оно относится только к пара- и диамагнетикам. 

24. Магнитное поле в веществе. Магнитные моменты атомов. Намагниченность. Макро- и микротоки.

Экспериментальные исследования показали, что все вещества в большей или меньшей степени обладают магнитными свойствами. Если два витка с токами поместить в какую-либо среду, то сила магнитного взаимодействия между токами изменяется. Этот опыт показывает, что индукция магнитного поля, создаваемого электрическими токами в веществе, отличается от индукции магнитного поля, создаваемого теми же токами в вакууме.

Физическая величина, показывающая, во сколько раз индукция   магнитного поля в однородной среде отличается по модулю от индукции  (0) магнитного поля в вакууме, называется магнитной проницаемостью: 

Магнитные свойства веществ определяются магнитными свойствами атомов или элементарных частиц (электронов, протонов и нейтронов), входящих в состав атомов.

Для качественного объяснения магнитных явлений с достаточным приближением можно считать, что электрон движется в атоме по круговым орбитам. Электрон, движущийся по одной из таких орбит, эквивалентен круговому току, поэтому он обладает орбитальным магнитным моментом p_m=ISn, модуль которого: где I=en — сила тока, n — частота вращения электрона по орбите, S — площадь орбиты. Если электрон движется по часовой стрелке, то ток направлен против часовой стрелки.

Намагниченность — векторная физическая величина, характеризующая магнитное состояние физического тела. Определяется как магнитный момент единицы объёма вещества:

Здесь, M — вектор намагниченности; m - вектор магнитного момента; V — объём.

В общем случае (случае неоднородной, по тем или иным причинам, среды) намагниченность выражается как:

Связь между M и напряженностью магнитного поля H в диамагнитных и парамагнитных материалах, обычно линейна (по крайней мере, при не слишком больших величинах намагничивающего поля): , где χ_m называют магнитной восприимчивостью.

Мы будем различать макроскопические токи, т.е. электрические токи, протекающие по проводникам в электрических цепях и микроскопические токи, обусловленных движением электронов в атомах и молекулах.

Внешнее магнитное поле оказывает ориентирующее, упорядочивающее действие на эти микротоки. Например, если вблизи какого-то тела поместить проводник с током (макроток), то под действием его магнитного поля микротоки во всех атомах определенным образом ориентируются, создавая в теле дополнительное магнитное поле. Вектор магнитной индукции B характеризует результирующее магнитное поле, создаваемое всеми макро- и микротоками. Поэтому, при одном и том же макротоке, вектор B в различных средах будет иметь разные значения. Магнитное поле макротока описывается вектором напряженности магнитного поля H.

В среде магнитное поле макротоков усиливается за счет поля микротоков среды.