21. Явление электромагнитной индукции. Законы Фарадея-Максвелла. Правило Ленца. Вывод закона электромагнитной индукции на основе электронной теории.

Электромагнитная индукция (индукция значит наведение) это явление, при котором в замкнутом контуре возникает электрический ток при изменении магнитного потока, пронизывающего его.

Явление электромагнитной индукции было обнаружено в 1831 г.

М. Фарадеем. Ток, возникающий при электромагнитной индукции, называют индукционным.

Закон электромагнитной индукции: ЭДС индукции в контуре равна скорости изменения магнитного потока сквозь поверхность, ограниченную контуром: .

Согласно закону электромагнитной индукции Фарадея знак «минус» означает, что ЭДС индукции действует так, что индукционный ток препятствует изменению потока. Этот факт и отражён в правиле Ленца.

Правило Ленца определяет направление индукционного тока и гласит:

Индукционный ток всегда имеет такое направление, что он ослабляет действие причины, возбуждающей этот ток.

[ВЫВОД ЗАКОНА ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ НА ОСНОВЕ ЭЛЕКТРОННОЙ ТЕОРИИ].

22. Явление самоиндукции. Токи замыкания и размыкания. Взаимная индукция.

Самоиндукция — возникновение ЭДС индукции в замкнутом проводящем контуре при изменении тока, протекающего по контуру.

При изменении тока в контуре пропорционально меняется и магнитный поток через поверхность, ограниченную этим контуром. Изменение этого магнитного потока, в силу закона электромагнитной индукции, приводит к возбуждению в этом контуре индуктивной ЭДС.

Это явление и называется самоиндукцией.

Направление ЭДС самоиндукции всегда оказывается таким, что при возрастании тока в цепи ЭДС самоиндукции препятствует этому возрастанию (направлена против тока), а при убывании тока — убыванию (сонаправлена с током).

Величина ЭДС самоиндукции пропорциональна скорости изменения силы тока  :

.

Коэффициент пропорциональности   называется коэффициентом самоиндукции или индуктивностью контура (катушки).

Рассмотрим процесс выключения тока в цепи, содержащей источник тока с э.д.с.  , резистор сопротивлением R и катушку индуктивностью L. Под действием внешней э.д.с. в цепи течет постоянный ток .

В момент времени t=0 отключим источник тока. Ток в катушке индуктивностью L начнет уменьшаться, что приведет к возникновению э.д.с. самоиндукции  препятствующей, согласно правилу Ленца, уменьшению тока. В каждый момент времени ток в цепи определяется законом Ома I= /R, или

Разделив в выражении переменные, получим  . Интегрируя это уравнение по I (от I₀ до I) и t (от 0 до t), находим где t=L/R ≈ постоянная, называемая временем релаксации. Из полученного выражения следует, что t есть время, в течение которого сила тока уменьшается в е раз.

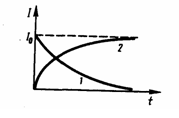
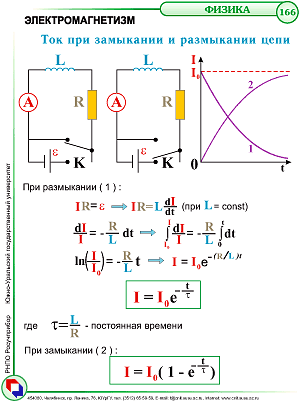
Таким образом, в процессе отключения источника тока сила тока убывает по экспоненциальному закону и определяется кривой 1 на рисунке. Чем больше индуктивность цепи и меньше ее сопротивление, тем больше t и, следовательно, тем медленнее уменьшается ток в цепи при ее размыкании.

При замыкании цепи помимо внешней э.д.с.  возникает э.д.с. самоиндукции  препятствующая, согласно правилу Ленца, возрастанию тока. По закону Ома,  или

Введя новую переменную  преобразуем это уравнение к виду где t ≈ время релаксации.

В момент замыкания (t=0) сила тока I = 0 и u = √  . Следовательно, интегрируя по u (от √  до IR√ ) и t (от 0 до t), находим где  ≈ установившийся ток.

Таким образом, в процессе включения источника тока нарастание силы тока в цепи определяется кривой 2 на рисунке. Сила тока возрастает от начального значения I=0 и асимптотически стремится к установившемуся значению  .Скорость нарастания тока определяется тем же временем релаксации t=L/R, что и убывание тока. Установление тока происходит тем быстрее, чем меньше индуктивность цепи и больше ее сопротивление.

Взаимоиндукция (взаимная индукция) — возникновение электродвижущей силы (ЭДС индукции) в одном проводнике вследствие изменения силы тока в другом проводнике или вследствие изменения взаимного расположения проводников. При изменении тока в одном из проводников или при изменении взаимного расположения проводников происходит изменение магнитного потока через воображаемую поверхность, "натянутую" на контур второго, созданного магнитным полем, порожденным током в первом проводнике, что по закону электромагнитной индукции вызывает возникновение ЭДС во втором проводнике. Если второй проводник замкнут, то под действием ЭДС взаимоиндукции в нём образуется индуцированный ток. И наоборот, изменение тока во второй цепи вызовет появление ЭДС в первой. Направление тока, возникшего при взаимоиндукции, определяется по правилу Ленца. Правило указывает на то, что изменение тока в одной цепи (катушке) встречает противодействие со стороны другой цепи (катушки).

Чем большая часть магнитного поля первой цепи пронизывает вторую цепь, тем сильнее взаимоиндукция между цепями. С количественной стороны явление взаимоиндукции характеризуется взаимной индуктивностью (коэффициентом взаимоиндукции, коэффициентом связи). Для изменения величины индуктивной связи между цепями, катушки делают подвижными.

[ ].