Фигура и модели Земли

С

Рис. 1.1. Геоид

уда совершают плавания по водам Мирового океана на поверхности Земли. Поэтому для морской навигации необходимо знать форму и размер Земли. Форма Земли уникальна и не совпадает ни с одной из известных геометрических форм. Неправильность формы Земли обусловлена неравномерным распределением плотности масс в её толще. Фигура Земли называется геоидом. В переводе с греческого геоид означает “землеподобный” (рис. 1.1). Геоид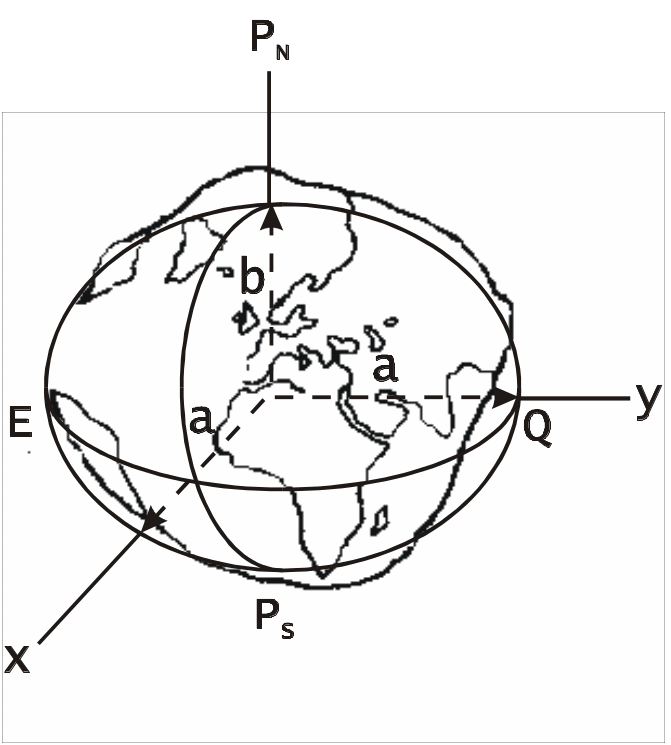 это неправильное геометрическое тело, ограниченное уровенной поверхностью океанов при полном равновесии, находящихся в них, водных масс. Эта уровенная поверхность всюду горизонтальна, т.е. в любой точке нормаль к ней совпадает с отвесной линией; она непрерывная, замкнутая, без складок и рёбер. Геометрия геоида очень сложна и из-за этого обработка измерений, относимых к его поверхности, очень затруднена. Поэтому для решения задач судовождения пользуются наиболее близким к геоиду телом правильной математической формы - эллипсоидом вращения, образованным вращением эллипса вокруг малой оси.

Общеземной эллипсоид удовлетворяет следующим условиям:

1. объем эллипсоида равен объёму геоида;

2. большая полуось эллипсоида a совпадает с плоскостью экватора геоида;

3. малая полуось b совпадает с осью вращения геоида;

4. сумма квадратов уклонений поверхности эллипсоида от поверхности геоида выбрана минимальной.

Общеземной эллипсоид практически совпадает со сфероидом - фигурой равновесия вращающейся жидкой массы. Разность по высоте их поверхностей составляет всего 2-3 метра. Поэтому понятие “земной сфероид” и “земной эллипсоид” тождественны. Вид земного сфероида характеризуется полярным сжатием, т.е. отношением разности полуосей эллипсоида к большой полуоси

(1.1)

Вместо полярного сжатия часто пользуются эксцентриситетом

(1.2)

или его квадратом

(1.3)

Связь  и е:

, , .

Следовательно

, , ,

или приближённо

e²  2.

Используя уравнения эллипсоида вращения, можно сравнительно просто математически обработать измерения, произведённые на поверхности Земли.

Из-за различия фигур геоида и эллипсоида вращения нельзя подобрать эллипсоид, который одинаково совпадал бы с геоидом во всех точках уровенной поверхности. Поэтому в разных странах за фигуру Земли принимают такие эллипсоиды, размеры которых в наибольшей степени совпадают с геоидом на территории данной страны.

Эллипсоид с определёнными размерами, определённым образом ориентированный в теле Земли, к поверхности которого относятся результаты геодезических и топографических работ в государстве называется референц-эллипсоидом.

Из-за различия референц-эллипсоидов координаты одних и тех же точек на картах, изданных в разных странах, могут не совпадать. Поэтому переход с карты на карту должен осуществляться не по координатам, а по пеленгу и расстоянию до какого-либо точечного ориентира, нанесённого на обеих картах.

В СССР до 1946 г. использовался референц-эллипсоид Бесселя, выведенный ещё в 1841 г. В России используется референц-эллипсоид Ф.Н.Красовского, имеющий следующие параметры:

1. большая полуось a = 6 378 245 м;

2. малая полуось b = 6 356 863 м;

3. полярное сжатие

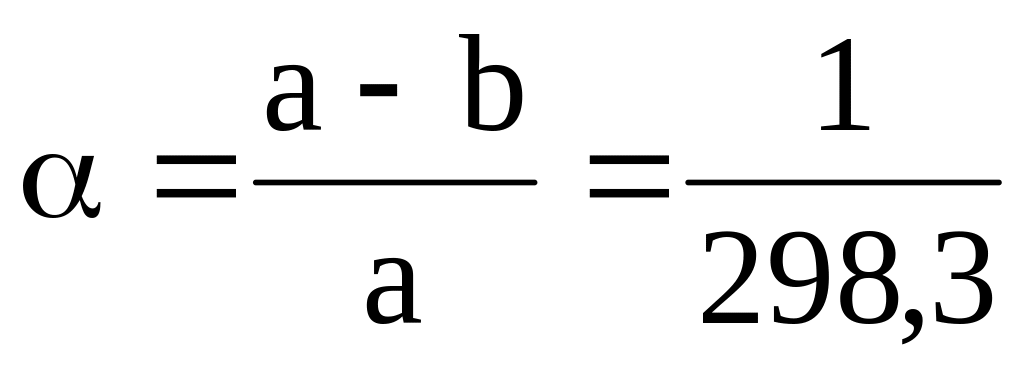
4. эксцентриситет .

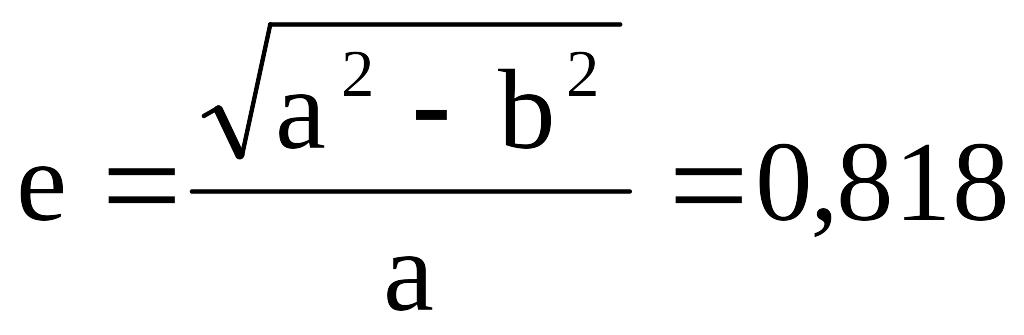Максимальное отклонение данного эллипсоида от геоида на территории России не превышает 150 м.

Для решения задач определения места судна с помощью глобальных радионавигационных и спутниковых систем используются международные референц-эллипсоиды, у которых отклонения от поверхности геоида в целом минимальны.

В спутниковых навигационных системах (СНС) первого поколения (Транзит, Цикада) использовался эллипсоид WGS - 72 (World Geodetic System - 1972), в настоящее время применяется более точные модели WGS – 84 в СНС GPS (NAVSTAR) и ПЗ-90 (PZ-90) в СНС ГЛОНАСС. Последние исследования показали, что Земля имеет форму апиоида (pear – груша).

Если на судне используются координаты, полученные по автоматизированному приёмоиндикатору радионавигационной или спутниковой систем и рассчитанные на усреднённом международном эллипсоиде, то для определения места судна на навигационной карте, составленной на другом референц-эллипсоиде, необходимо ввести поправки к таким координатам. Подробнее об этом см. в п. ...

При решении задач навигации, не требующих высокой точности, Землю принимают за шар, объём которого равен объёму земного эллипсоида:

(1.4)

Отсюда для референц-эллипсоида Ф.Н.Красовского радиус Земли, как шара, равен R= 6 371 110м.