Билет №23 «Ширина спектральных линий.Мультиплетность спектров.Спин электрона.Магнетон Бора»

• ШИРИНА СПЕКТРАЛЬНЫХ ЛИНИЙ, интервал частот v (или длин волн l=c/v), характеризующий спектр. линии в спектрах оптических атомов, молекул и др. квант. систем. Каждому излучательному квантовому переходу между дискр. уровнями энергии ξ_k н ξ_i соответствует нек-рый интервал Dn_ki частот, близких к частоте перехода n_ki=(ξ_k-ξ_i)/h=(ξ_k-ξi)/2pћ. Значение Dn_ki определяет Ш. с. л.— степень немонохроматичности данной спектр. линии. Контур спектр. линии I(n) (зависимость интенсивности испускания или поглощения от частоты) обычно имеет максимум при частоте перехода n_ki

• Рассмотрим на примере атома натрия, как существование спина электрона может объяснить мультиплетную структуру спектра. Поскольку момент атомного остатка равен нулю, момент атома натрия равен моменту оптического электрона. Момент же электрона будет слагаться из двух моментов: орбитального M_if обусловленного движением электрона в атоме, и спинового M_St не связанного с движением электрона в прастранстве. Результирующая этих двух моментов дает полный момент импульса оптического электрона. Сложение орбитального и спинового моментов в полный момент осуществляется по тем же квантовым законам, по которым складываются орбитальные моменты разных электронов [см. (70.2)]. Величина полного момента Доопределяется квантовым числом /;

Составляющая механического момента по заданному направлению может принимать квантованные значения, отличающиеся друг от друга на Ь:

Чтобы найти величину собственного магнитного момента электрона, умножим M_s на отношение (72,2) \i_s к M_s:

Знак минус указывает на то, что механический М₃ и магнитный |i₃ моменты электрона направлены в противоположные стороны.

Проекция собственного магнитного момента электрона на заданное направление может иметь следующие значения:

(72.5)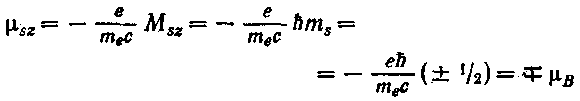 (72.6)

причем / может иметь значения:

где / и s соответственно азимутальное и спиновое квантовые числа. При 1 = 0 квантовое число / имеет только одно значение: . При /, отличном от нуля, возможны два значения: и , которые соответствуют двум возможным взаимным ориентациям моментов Mi и M_s — «параллельной» и «антипараллельной» ) §131).

Спин электрона (и всех других микрочастиц) — квантовая величина, у нее нет классического аналога; это внутреннее неотъемлемое свойство электрона, подобное его заряду и массе.

Если электрону приписывается собственный механический момент импульса (спин) L_s, то ему соответствует собственный магнитный момент р_ms. Согласно общим выво­дам квантовой механики, спин квантуется по закону

где s — спиновое квантовое число.

По аналогии с орбитальным моментом импульса, проекция L_sz спина квантуется так, что вектор L_s может принимать 2s+1 ориентации. Так как в опытах Штерна и Герлаха наблюдались только две ориентации, то 2s+1=2, откуда s= ½ . Проекция спина на направление внешнего магнитного поля, являясь квантованной величиной, определяется выражением, аналогичным (223.6):

где т_s — магнитное спиновое квантовое число; оно может иметь только два значения: m_s = ± ½ .

• Магнето́н Бо́ра — единица элементарного магнитного момента магнетон Бора определяется как

и в системе СИ как

,где ħ — постоянная Планка, е — элементарный электрический заряд, m_e — масса электрона, c - скорость света.

Физический смысл величины μ_B легко понять из полуклассического рассмотрения движения электрона по круговой орбите радиуса r со скоростью v. Такая система аналогична витку с током, сила I которого равна заряду, делённому на период вращения: I = ev /2πr. Магнитный момент электрона кратен магнетону Бора.