лептоны — фермионы, которые имеют вид точечных частиц (т. е. не состоящих ни из чего) вплоть до масштабов порядка 10⁻¹⁸ м.

кварки — дробнозаряженные частицы, входящие в состав адронов.

калибровочные бозоны — частицы, посредством обмена которыми осуществляются взаимодействия:

• фотон — частица, переносящая электромагнитное взаимодействие;

• восемь глюонов — частиц, переносящих сильное взаимодействие;

• три промежуточных векторных бозона W⁺, W⁻ и Z⁰, переносящие слабое взаимодействие;

• гравитон — гипотетическая частица, переносящая гравитационное взаимодействие

Билет №30 «Электропроводность металлов.Сверхпроводимсоть.Температурные зависимости проводимости»

теория электропроводности, основы­вающаяся на квантовой механике и квантовой статистике Ферми — Дирака, — пере­смотрела вопрос об электропроводности металлов, рассмотренный в классической физике. Расчет электропроводности металлов, выполненный на основе этой теории, приводит к выражению для удельной электрической проводимости металла

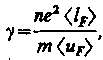
п — концентрация электронов прово­димости в металле, ál_Fñ — средняя длина свободного пробега электрона, имеющего энергию Ферми, áu_Fñ — средняя скорость теплового движения такого электрона.

Общность эффектов, наблюдаемых в сверхпроводящем состоянии различных ме­таллов, их соединений и сплавов, указывает на то, что явление сверхпроводимости обусловлено физическими причинами, общими для различных веществ, т. е. должен существовать единый для всех сверхпроводников механизм этого явления.

Качественно явление сверхпроводимости можно объяснить так. Между электрона­ми металла помимо кулоновского отталкивания, в достаточной степени ослабляемого экранирующим действием положительных ионов решетки, в результате электрон-фононного взаимодействия (взаимодействия электронов с колебаниями решетки) воз­никает слабое взаимное притяжение. Это взаимное притяжение при определенных условиях может преобладать над отталкиванием. В результате электроны проводимо­сти, притягиваясь, образуют своеобразное связанное состояние, называемое куперовской парой. «Размеры» пары много больше (примерно на четыре порядка) среднего межатомного расстояния, т. е. между электронами, «связанными» в пару, находится много «обычных» электронов.

Билет №31 «Дырочня проводимость.ПРимесная проводимость.Зпрещенные зоны.Валентная зона.Зона проводимости»

Проводимость полупроводников, обусловленная примесями, называется примесной проводимостью, а сами полупроводники — примесными полупроводниками. Примесная проводимость обусловлена примесями (атомы посторонних элементов), а также дефек­тами типа избыточных атомов (по сравнению со стехиометрическим составом), тепло­выми (пустые узлы или атомы в междоузлиях) и механическими (трещины, дислокации и т. д.) дефектами. Наличие в полупроводнике примеси существенно изменяет его проводимость.

, в полупроводниках с примесью, валентность которой на единицу больше валентности основных атомов, носителями тока являются электроны; воз­никает электронная примесная проводимость (проводимость n-типа). Полупроводники с такой проводимостью называются электронными (или полупроводниками n-типа). Примеси, являющиеся источником электронов, называются донорами, а энергетические уровни этих примесей — донорными уровнями.

в полупроводниках с примесью, валентность которой на единицу меньше валентности основных атомов, носителями тока являются дырки; возникает дырочная проводимость (проворность p-типа). Полупроводники с такой проводимостью называются дырочными (или полупроводниками p-типа). Примеси, захватывающие электроны из валентной зоны полупроводника, называются акцепторами, а энергети­ческие уровни этих примесей — акцепторными уровнями.

Энергия внешних электронов может принимать значения в пределах, называемых разрешенными энергетическими зонами. Каждая разрешенная зона «вмещает» в себя столько близлежащих дискретных уровней, сколь­ко атомов содержит кристалл: чем больше в кристалле атомов, тем теснее рас­положены уровни в зоне. Расстояние между соседними энергетическими уровнями в зоне составляет приблизительно 10^–22 эВ. Так как оно столь ничтожно, то зоны можно считать практически непрерывными, однако факт конечного числа уровней в зоне играет важную роль для распределения электронов по состояниям.

Разрешенные энергетические зоны разделены зонами запрещенных значений энер­гии, называемыми запрещенными энергетическими зонами. В них электроны находиться не могут. Ширина зон (разрешенных и запрещенных) не зависит от размера кристалла. Разрешенные зоны тем шире, чем слабее связь валентных электронов с ядрами.

Билет №32 «Работа выхода.Термоэлектронная эмиссия.Контактная разность потенциалов»

Термоэлектро́нная эми́ссия явление испускания электронов нагретыми телами. Концентрация свободных электронов в металлах достаточно высока, поэтому даже при средних температурах вследствие распределения электронов по скоростям (по энергии) некоторые электроны обладают энергией, достаточной для преодоления потенциального барьера на границе металла. С повышением температуры число электронов, кинетическая энергия теплового движения которых больше работы выхода, растет, и явление термоэлектронной эмиссии становится заметным.

свободные электроны при обычных температурах практически не покидают металл. Следовательно, в поверхностном слое металла должно быть задерживающее электрическое поле, препятствующее выходу электронов из металла в окружающий вакуум. Работа, которую нужно затратить для удаления электрона из металла в вакуум, называется работой выхода. Укажем две вероятные причины появле­ния работы выхода:

Разность потенциалов Dj в этом слое, называемая поверхностным скачком потенциала, определяется работой выхода (А) электрона из металла:

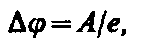
где е — заряд электрона. Так как вне двойного слоя электрическое поле отсутствует, то потенциал среды равен нулю, а внутри металла потенциал положителен и равен Dj. Потенциальная энергия свободного электрона внутри металла равна —еDj и является относительно вакуума отрицательной.

Работа выхода выражается в электрон-вольтах

Работа выхода зависит от химической природы металлов и от чистоты их поверх­ности

Вольта экспериментально установил два закона:

1. Контактная разность потенциалов зависит лишь от химического состава и тем­пературы соприкасающихся металлов.

2. Контактная разность потенциалов последовательно соединенных различных проводников, находящихся при одинаковой температуре, не зависит от химического состава промежуточных проводников и равна контактной разности потенциалов, воз­никающей при непосредственном соединении крайних проводников.

разность потенциалов, равна

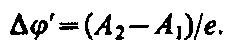
Разность потенциалов обусловленная различием работ выхода контактиру­ющих металлов, называется внешней контактной разностью потенциалов. Чаще говорят просто о контактной разности потенциалов, подразумевая под ней внешнюю.

Если уровни Ферми для двух контактирующих металлов не одинаковы, то между внутренними точками металлов наблюдается внутренняя контактная разность потенци­алов, которая, как следует из рисунка, равна

Билет №33 «Контактные явления в полупроводниках»

КОНТАКТНЫЕ ЯВЛЕНИЯ В ПОЛУПРОВОДНИКАХ - неравновесные электронные явления, возникающие при прохождении электрич. тока через контакт полупроводника с металлом или электролитом или через контакт двух различных полупроводников (гетеропереход)либо через границу двух областей одного и того же полупроводника с разным типом носителей заряда и разной их концентрацией.

Приведение в контакт двух разл. материалов сопровождается перетеканием носителей (для определённости электронов) из одного в другой и образованием контактной разности потенциалов V_K. Напряжённость поля контактной разности потенциалов плавно убывает в глубь полупроводника, вызывая приконтактный изгиб краёв энергетич. зон (валентной зоны и зоны проводимости). Направление изгиба и его величина зависят от знака и величины V_K, определяемой разностью работ выхода, а также от знака и концентрации локализованных на поверхности раздела зарядов (адсорбированные ионы, заряженные поверхностные дефекты и др., см. ниже).

Инжекция становится заметной, если плотность тока

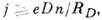(1)

где n - концентрация электронов основных носителей заряда в полупроводнике, D - их коэф. диффузии, R_D - дебаевский радиус экранирования, е - элементарный заряд. С ростом тока проводимость полупроводника всё более определяется инжектированными электронами, рост концентрации к-рых ограничивается их объёмным зарядом (токи, ограниченные пространств. зарядом). В результате проводимость образца становится существенно нелинейной. Электрич. сопротивление омич. контакта с обогащённым слоем увеличивается при наличии диэлектрич. прослойки Д между металлом и полупроводником (напр., окисла металла, рис. 3). Из-за туннельной проницаемости прослойки проводимость её при малых толщинах А) становится пренебрежимо большой. В прослойке, а также на границе окисел-полупроводник, как правило, возникают центры захвата носителей заряда, поле к-рых наряду с полем контактной разности потенциалов управляет приконтактным изгибом зон, существенно изменяя его величину, а иногда и знак.Это приводит к нестабильности и невоспроизводимости омич. контактов металл-полупроводник.

Билет №34 «Термоэлектрические явления»

Согласно второму закону Вольта, в замкнутой цепи, состоящей из нескольких металлов, находящихся при одинаковой температуре, э.д.с. не возникает, т. е. не происходит возбуждения электрического тока. Однако если температура контактов не одинакова, то в цепи возникает электрический ток, называемый термоэлектрическим. Явление возбуждения термоэлектрического тока (явление Зеебека), а также тесно связанные с ним явления Пельте и Томсона называются термоэлектрическими явлениями.0

1. Явление Зеебека. В замкнутой цепи, состоящей из последовательно соединенных разнородных провод­ников, контакты между которыми имеют различную температуру, возникает элект­рический ток.

электродвижущая сила прямо пропор­циональна разности температур в контактах:

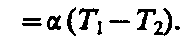
Эта э.д.с. называется термоэлектродвижущей силой.

Причина возникновения термоэлектродвижущей э.д.с. ясна из формулы, определяющей внутреннюю контактную разность потенциалов на границе двух металлов. Сумма скачков потенциала отлична от нуля, это приво­дит к возникновению термоэлектрического тока.

Явление Зеебека используется для измерения температуры. Для этого применяются термоэлементы, или термопары—датчики температур, состоящие из двух соединенных между собой разнородных металлических проводников. Чувствительность термопар выше, если их соединять последовательно.

2. Явление Пельтье при прохождении через контакт двух различных проводников электрического тока в зависимости от его направления помимо джоулевой теплоты выделяется или поглощается дополнительная теплота. Таким образом, явление Пельтье является обратным по отношению к явлению Зеебека. В отличие от джоулевой теплоты, которая пропорциональна квадрату силы тока, теплота Пельтье пропорциональна первой степени силы тока и меняет знак при изменении направления тока.

3. Явление Томсона при прохожде­нии тока по неравномерно нагретому проводнику должно происходить дополнительное выделение (поглощение) теплоты, аналогичной теплоте Пельтье. Так как в более нагретой части проводника электроны имеют большую среднюю энергию, чем в менее нагретой, то, двигаясь в направлении убывания температуры, они отдают часть своей энергии решетке, в результате чего происходит выделение теплоты Томсона. Если же электроны движутся в сторону возрастания температуры, то они, наоборот, пополняют свою энергию за счет энергии решетки, в результате чего происходит поглощение теплоты Томсона.

Билет №35 «Основные свойства атомного ядра»

Э. Резерфорд, атомные ядра имеют размеры примерно 10^–14 — 10^–15 м (линейные размеры атома примерно 10^–10 м).

Атомное ядро состоит из элементарных частиц — протонов и нейтронов

Протон (р) имеет положительный заряд, равный заряду электрона, и массу покоя т_р=1,6726×10^–27кг » 1836 т_e, где т_e — масса электрона. Нейтрон (n) — нейтральная частица с массой покоя т_п=1,6749×10^–27кг »1839 т_e. Протоны и нейтроны называют­ся нуклонами (от лат. nucleus — ядро). Общее число нуклонов в атомном ядре называ­ется массовым числом А.

Атомное ядро характеризуется зарядом Ze, где Z — зарядовое число ядра, равное числу протонов в ядре и совпадающее с порядковым номером химического элемента в Периодической системе элементов Менделеева

Так как атом нейтрален, то заряд ядра определяет и число электронов в атоме. Заряд ядра определяет специфику данного химического элемента, т.е. определяет число электро­нов в атоме, конфигурацию их электронных оболочек, величину и характер внутри­атомного электрического поля.

Ядра с разными числами нейтронов N=A–Z называются изотопами, а ядра с одинаковыми А, но разными Z—изобарами. Радиус ядра задается эмпирической формулой

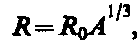
где R₀=(1,3¸1,7)10^–15 м. Однако при употреблении этого понятия необходимо со­блюдать осторожность (из-за его неоднозначности, например из-за размытости гра­ницы ядра). Из формулы вытекает, что объем ядра пропорционален числу нуклонов в ядре. Следовательно, плотность ядерного вещества примерно одинакова для всех ядер (»10¹⁷ кг/м³).

Билет №36 «Масса и энергия связи.Дефект массы.Деление тяжелых и синтез легких ядер»

Массу ядер очень точно можно определить с помощью масс-спектрометров — из­мерительных приборов, разделяющих с помощью электрических и магнитных полей пучки заряженных частиц (обычно ионов) с разными удельными зарядами Q/m. Масс-спектрометрические измерения показали, что масса ядра меньше, чем сумма масс составляющих его нуклонов.

Энергия, которую необходимо затратить, чтобы расщепить ядро на отдельные нуклоны, называется энергией связи ядра .

для энергии связи ядра пользуются формулой

где m_H — масса атома водорода. Так как m_H больше m_p на величину m_e, то первый член в квадратных скобках включает в себя массу Z электронов. Но так как масса атома т отличается от массы ядра т_я как раз на массу Z электронов, то вычисления по формулам приводят к одинаковым результатам.

Величина

называется дефектом массы ядра. На эту величину уменьшается масса всех нуклонов при образовании из них атомного ядра.

Часто вместо энергии связи рассматривают удельную энергию связи dE_св — энер­гию связи, отнесенную к одному нуклону. Она характеризует устойчивость (прочность) атомных ядер, т. е. чем больше dE_св, тем устойчивее ядро.

наиболее устойчивыми с энергетической точки зрения являются ядра средней части таблицы Менделеева. Тяжелые и легкие ядра менее устойчивы.

Билет №37 «Ядерные силы.Модели ядра.Мезоны»

ядерные силы - особые, специфические для ядра силы, значительно превышающие кулоновские силы отталкивания между протонами.

Ядерные силы относятся к классу так называемых сильных взаимодействий.

Перечислим основные свойства ядерных сил:

1) являются силами притяжения;

2) являются короткодействующими — их действие проявляется то­лько на расстояниях примерно 10^–15 м.

3) свойственна зарядовая независимость: ядерные силы имеют неэлектрическую природу;

4) свойственно насыщение,

5) зависят от взаимной ориентации спинов взаимодействующих нуклонов.

6) не являются центральными

Капельная модель ядра основана на аналогии между поведением нуклонов в ядре и поведением молекул в капле жидкости. Существенное отличие ядра от капли жидкости в этой модели заключается в том, что она трактует ядро как каплю электрически заряженной несжимаемой жидкости (с плотностью, равной ядер­ной), подчиняющуюся законам квантовой механики.

2. Оболочечная модель ядра Оболочечная модель пред­полагает распределение нуклонов в ядре по дискретным энергетическим уровням (оболочкам), заполняемым нуклонами согласно принципу Паули, и связывает устой­чивость ядер с заполнением этих уровней. Считается, что ядра с полностью заполнен­ными оболочками являются наиболее устойчивыми.

обобщенная модель ядра (синтез капельной и оболочечной моделей),

оптическая модель ядра (объясняет взаимодействие ядер с налетающими частицами)

Нейтральный пион распадается на два g-кванта:

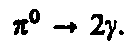
Существуют положительный (p⁺), отрицательный (p^–) (их заряд равен элементар­ному заряду е) и нейтральный (p⁰) мезоны.

Распад заряженных пионов происходит в основном по схемам

Билет №38 «Радиоактивность.Постоянная распада.Альфа,бета и гамма-излучения»

Радиоактивность - способность некоторых атом­ных ядер самопроизвольно (спонтанно) превращаться в другие ядра с испусканием различных видов радиоактивных излучений и элементарных частиц. Радиоактивность подразделяется на естественную и искусственную. Принципиального различия между этими двумя типами радиоактив­ности нет, так как законы радиоактивного превращения в обоих случаях одинаковы.

Радиоактивное излучение бывает трех типов: a-, b- и g-излучение.

a-Излучение отклоняется электрическим и магнитным полями, обладает высокой ионизирующей способностью и малой проникающей способностью

b-Излучение отклоняется электрическим и магнитным полями; его ионизирующая способность значительно меньше, а проникающая способ­ность гораздо больше, чем у a-частиц. b-Излучение представляет собой поток быстрых электронов

g-Излучение не отклоняется электрическим и магнитным полями, обладает от­носительно слабой ионизирующей способностью и очень большой проникающей спо­собностью g-Излучение представляет собой корот­коволновое электромагнитное излучение с чрезвычайно малой длиной волны l<10^–10 м и вследствие этого — ярко выраженными корпускулярными свойствами, т.е. является потоком частиц — g-квантов (фотонов).

Теория радиоактивного распада строится на предположении о том, что радиоак­тивный распад является спонтанным процессом, подчиняющимся законам статистики:

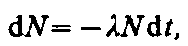
где l — постоянная для данного радиоактивного вещества величина, называемая постоянной радиоактивного распада; знак минус указывает, что общее число радиоак­тивных ядер в процессе распада уменьшается.

Суммарная продолжительность жизни dN ядер равна t|dN|=lNtdt. Проинтег­рировав это выражение по всем возможным t (т. е. от 0 до ¥) и разделив на началь­ное число ядер N₀, получим среднее время жизни t радиоактивного ядра:

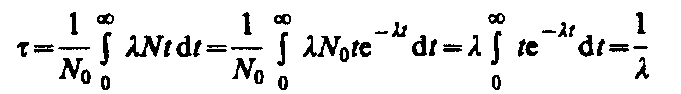
Таким образом, среднее время жизни t радиоактивного ядра есть величина, обратная постоянной радиоактивного распада l.