
«Истончённый» гармонический ряд Править
Ряд Кемпнера (англ.)
Если рассмотреть гармонический ряд, в котором оставлены только слагаемые, знаменатели которых не содержат цифры 9, то окажется, что оставшаяся сумма сходится к числу <80, точнее — к 22,92067 66192 64150 34816. Более того, доказано, что если оставить слагаемые, не содержащие любой заранее выбранной последовательности цифр, то полученный ряд будет сходиться.
Учитывая сходимость Ряда Кемпнера можно предположить что сходимость гармонического ряда хотя пока и не доказана, но имеет место быть! (см. обсужд.)
В пользу сходимости гармонического ряда свидетельствует и такой мысленный эксперимент: запишем три столбца,
№ п/п строки Частичная Сумма гармонического геометрическая прогрессияс коэффициентом,
(натуральное) ( ряда, до члена 1/n ) например ((256 в степени 256)-1)/(256 в степени 256)
1 1 ((256 в степени 256)-1)/(256 в степени 256) 2 1+1/2 +((256 в степени 256)-1)/(256 в степени 256)^2 3 1/3+1/2+1 +((256 в степени 256)-1)/(256 в степени 256)^3 . . ... . 256 1+1/2+1/3 + ...+ 1/256 +((256 в степени 256)-1)/(256 в степени 256)^256 ... (256 в степени 256) 1+1/2+...+1/(256^256) +((256^256)-1)^(256-1)^256)) ^((256^256)-1)^(256-1)^256))
(256 в степени 256) +1)) .... ...
...
Очевидно, что для любого натурального, стермящегося к бесконечности, всегда найдется такое натуральное+1, которое будучи разделенным на то же самое натуральное +2 даст такой коэффициент, который будет меньше единицы и обеспечит сходимость суммы членов ряда геометрической прогрессии, каждый из которыхзаведомо меньше соответствующего (с таким же номером), члена гармонического ряда.
29.Признак сходимости Даламбера
Пусть дан знакоположительный числовой ряд
![]() (7)
(7)
и
пусть существует предел ![]() При p<1
ряд (7) сходится, при p>1
ряд (7) расходится.
При p<1
ряд (7) сходится, при p>1
ряд (7) расходится.
Доказательство.
По условию существует предел ![]() .
Это означает, что для любого положительного
числа Е существует
такой номер N,
что для всех номеров n³N выполняется
условие
.
Это означает, что для любого положительного
числа Е существует
такой номер N,
что для всех номеров n³N выполняется
условие![]() или
или
p-E<![]() (10)
(10)
Пусть
сначала p<1.
Выберем Е так,
что p+E=q<1. Для
всех n³N имеем ![]()
![]()
![]() …
или
…
или
![]()
или
![]() (11)
(11)
Рассмотрим ряды
![]() (12)
(12)
![]() . (13)
. (13)
Ряд (13) сходится, так как он является бесконечно убывающей геометрической прогрессией. Тогда ряд (12) сходится, учитывая (11), по признаку сравнения. Ряд (7) сходится по теореме 1.
Пусть
теперь p>1.
Выберем Е так,
что p-E>1.
Тогда из левой части неравенства (10)
следует, что при n³N выполняется ![]() или un+1>un,
то есть члены ряда возрастают с
возрастанием номера n.
Поэтому
un¹0,
следовательно, ряд расходится по
следствию из необходимого признака
сходимости. Теорема доказана.
или un+1>un,
то есть члены ряда возрастают с
возрастанием номера n.
Поэтому
un¹0,
следовательно, ряд расходится по
следствию из необходимого признака
сходимости. Теорема доказана.
Замечания.
1. Если расходимость ряда установлена с помощью признака Даламбера, то un¹0.
2. При р=1 признак Даламбера не даёт ответа о сходимости ряда. В этом случае нужно применять другие признаки сходимости.
3. Признак Даламбера рекомендуется применять при наличии в выражении общего члена ряда показательной функции или факториала.
Пример.
Исследовать
на сходимость ряд ![]()
Применим
признак Даламбера. un=![]() un+1=
un+1=![]() =
=
![]() .
. ![]()
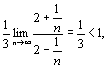 следовательно,
ряд сходится по признаку Даламбера.
следовательно,
ряд сходится по признаку Даламбера.
30.Признак сравнения рядов.
Признак сравнения — утверждение об одновременности расходимости или сходимости двух рядов, основанный на сравнении членов этих рядов.
Пусть даны два знакоположительных ряда:
![]() и
и ![]()
.
Тогда,
если, начиная с некоторого места (![]() ),
выполняется неравенство:
),
выполняется неравенство:
![]() ,
,
то из сходимости ряда следует сходимость .
Или же, если ряд расходится, то расходится и .
Признак сравнения отношений
Также признак сравнения можно сформулировать в более удобной форме — в виде отношений.
[править]Формулировка
Если для членов строго положительных рядов и , начиная с некоторого места ( ), выполняется неравенство:
то из сходимости ряда следует сходимость , а из расходимости следует расходимость . |
Предельный признак сравнения
Поскольку достоверно установить справедливость этого неравенства при любых n — довольно сложная задача, то на практике признак сравнения обычно используется в предельной форме.
[править]Формулировка
Если и есть строго положительные ряды и
то
при |
31.Признак Коши
1)Радикальный признак Коши — признак сходимости числового ряда:
Если для числового ряда
с
неотрицательными членами существует
такое число ![]() ,
, ![]() ,
что, начиная с некоторого номера,
выполняется неравенство
,
что, начиная с некоторого номера,
выполняется неравенство ![]() ,
то данный ряд сходится.
,
то данный ряд сходится.
Предельная форма
Условие радикального признака равносильно следующему:
![]()
То есть можно сформулировать радикальный признак сходимости знакоположительного ряда в предельной форме:
-
Если для ряда
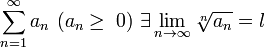 ,
то
,
тоесли
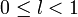 ряд
сходится,
ряд
сходится,если
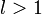 ряд
расходится,
ряд
расходится,если
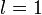 вопрос
о сходимости ряда остается открытым.
вопрос
о сходимости ряда остается открытым.
]Доказательство
1.
Пусть ![]() .
Очевидно, что существует такое
.
Очевидно, что существует такое ![]() ,
что
,
что ![]() .
Поскольку существует предел
.
Поскольку существует предел ![]() ,
то подставив в определение предела
выбранное
,
то подставив в определение предела
выбранное ![]() получим:
получим:
![]()
Раскрыв модуль, получаем:
![]()
![]()
![]()
Поскольку
,
то ряд ![]() сходится.
Следовательно, по признаку
сравнения ряд
тоже
сходится.
сходится.
Следовательно, по признаку
сравнения ряд
тоже
сходится.
2.
Пусть
.
Очевидно, что существует такое
,
что ![]() .
Поскольку существует предел
,
то подставив в определение предела
выбранное
получим:
.
Поскольку существует предел
,
то подставив в определение предела
выбранное
получим:
Раскрыв модуль, получаем:
Поскольку
,
то ряд ![]() расходится.
Следовательно, по признаку
сравнения ряд
тоже
расходится.
расходится.
Следовательно, по признаку
сравнения ряд
тоже
расходится.
Примеры
1. Ряд
![]()
сходится, так как выполняется условие предельной формы радикального признака теоремы Коши
![]()
2. Рассмотрим ряд
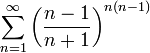
![]() ряд
сходится.
ряд
сходится.
2)Интегральный
признак Коши́-Макло́рена —
признак сходимости убывающего
положительного числового
ряда.
Признак Коши-Маклорена даёт возможность
свести проверку сходимости ряда к
проверке сходимости несобственного
интеграла соответствующей
функции на ![]() ,
последний часто может быть найден в
явном виде.
,
последний часто может быть найден в
явном виде.
Пусть для функции f(x) выполняется:
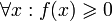 (функция
принимает неотрицательные значения)
(функция
принимает неотрицательные значения)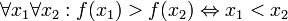 (функция
монотонно убывает)
(функция
монотонно убывает)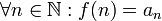 (соответствие
функции ряду)
(соответствие
функции ряду)
Тогда
ряд
и
несобственный интеграл 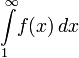 сходятся
или расходятся одновременно
сходятся
или расходятся одновременно
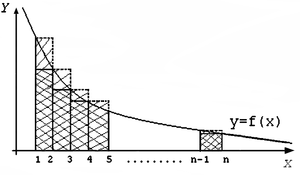
Построим на графике f(x) ступенчатые фигуры как показано на рисунке
Площадь большей фигуры равна
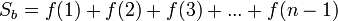
Площадь меньшей фигуры равна
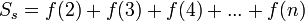
Площадь криволинейной трапеции под графиком функции равна
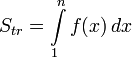
Получаем
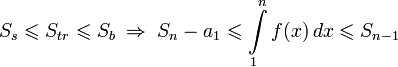
Далее доказывается с помощью критерия сходимости знакоположительных рядов.
