Свойства
Дисперсия
любой случайной величины неотрицательна: 
Если дисперсия случайной величины
конечна, то конечно и её математическое
ожидание; Если случайная величина равна
константе, то её дисперсия равна
нулю: 
Верно
и обратное: если 
то 
почти
всюду;
Дисперсия суммы двух случайных величин
равна:
,
где 
—
их ковариация;
Для дисперсии произвольной линейной
комбинации нескольких
случайных величин имеет место равенство:
,
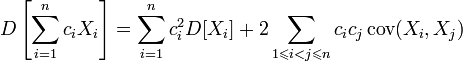где 
;
В частности, 
для
любых независимых или некоррелированных случайных
величин, так как их ковариации равны
нулю;
Вопрос 12.Вероятность появления хотя бы одного события. Теорема сложения вероятностей совместных событий.
Часть 1. Вероятность появления хотя бы одного события.
Пусть в результате испытаний могут появиться n событий, независимых в совокупности либо некоторые из них( в частности только одно или ни одного) причем вероятности появления каждого из событий известны. Как найти вероятность того, что наступит хотя бы одно из этих событий? Например если в результате испытания могут появиться хотя бы 3 события то появление хотя бы одного из этих событий означает наступление либо одного, либо двух либо 3 событий. Теорема: вероятность появления хотя бы одного из событий А1,А2,….,Аn независимых в совокупности равна разности между единицей и произведением вероятностей противоположных событий А1,А2,….,Аn
P(A)=1-q1,q2,….,qn
Доказательство. обозначим через А событие состоящее в появление отя бы одного из событий А1,А2,….,Аn. События А1,А2,….,Аn( ни одно из событий не наступило) противоположны следовательно сумма их вероятностей равна 1
P(A)+P(А1,А2,….,Аn)=1
Отсюда пользуясь теоремой умножения получим
P(A)=1- P(А1,А2,….,Аn)= 1-q1,q2,….,qn
В частности если события А1,А2,….,Аn имеют одинаковую вероятность равную p то вероятность появления хотя бы одного из этих событий P(A)=1-q в степени n.
Часть 2. Теорема сложения вероятностей совместных событий.
Теорема. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного наступления т.е.
P(A+B)=P(A)+P(B)-P(AB).Доказательство. Пусть в результате опыта возможны n равновозможных исходов. Пусть событию А благоприятствует m исходов, а событию
B – k исходов. События А и В совместны, поэтому часть указанных исходов благоприятствует и событию А, и событию В. Пусть количество таких исходов равно r. Тогда имеем : P(A)=m/n P(B)=k/n P(AB)=r/n
Событие А+В заключается в наступлении либо события А, либо события В, либо событию АВ, поэтому ему будут благоприятствовать m=k-r исходов. Тогда получим: P(A+B)=( m+k-r )/n =m/n+k/n-r/n Теорема доказана.
Вопрос 17.Локальная теорема Лапласа Свойства функции Гаусса.
Часть 1. Локальная теорема Лапласа.
Вероятность того, что в n независимых испытаниях , в каждом из которых вероятность появления события равна p(0<p<1) событие наступит ровно k раз (безразлично в какой последовательности) приближенно равна (тем точнее, чем больше n)
Вопрос 18.Интегральная теорема Лапласа. Свойства функции Лапласа.
Часть 1. Интегральная теорема Лапласа.
Вероятность того, что в n независимых испытаниях , в каждом из которых вероятность появления события равна p(0<p<1) событие наступит не менее а раз и не более b раз, приближенно равна
Здесь
Вопрос 20.Случайные величины.
Случайной называется величина, которая в результате испытаний может случайным
образом принять какие-либо числовые значения (пространство элементарных событий
случайной величины представляет собой множество чисел).
Дискретной называется случайная величина, значение которой образуют дискретный
набор чисел (конечной или счетной), т.е. все значения которой можно пронумеровать.
Непрерывной называется случайная величина, значения которой образуют некоторый
промежуток/промежутки числовой оси.
Пример:
1. бросание игральной кости: число выпавших очков – дискретная случайная
величина, принимающая значения 1, 2, 3…6
2. вес новорожденного: непрерывная случайная величина
3. расход электроэнергии за месяц: непрерывная случайная величина
4. число выстрелов сделанных охотником до попадания в мишень
Закон распределения случайной величины
Для дискретной случайной величины представляет собой таблицу в которой указаны его
значения
x x1 x2 … хn (…)
p p1 p2 … pn (…)
p1 + p2 +…+ pn = 1
pi ≥ 0
Функция распределения случайной величины
Это функция, значение которой в точке х равно вероятности того, что случайная величина
х принимает значение меньше х. f(x)=P{X<x}
Свойства функции распределения:
1. область определения F(x) (-∞; +∞)
2. область значений 0 ≤ F(x) ≤ 1
3. F(x)- монотонно возрастающая функция
lim x→+∞ F(x)=1
4.lim→−∞F(x)=0