Вопрос 23. Дифференциальная функция распределения
Плотность вероятности непрерывной случайной величины, она же дифференциальная функция распределения вероятностей - аналог закона распределения дискретной с.в. Но если закон распределения дискретной с.в. графически изображается в виде точек, соединённых для наглядности ломаной линией (многоугольник распределения), то плотность вероятностей графически представляет собой непрерывную гладкую линию (или кусочно-гладкую, если на разных отрезках задаётся разными функциями). Аналитически задаётся формулой. Если закон распределения дискретной с.в. ставит каждому значению x в соответствие определённую вероятность, то про плотность распределения такого сказать нельзя. Для непрерывных с.в. можно найти только вероятность попадания в какой-либо интервал. Считается, что для каждого отдельного (одиночного) значения непрерывной с.в. вероятность равна нулю. И графически вероятность попадания в интервал выражается площадью фигуры, ограниченной сверху графиком плотности вероятности, снизу осью ОХ, с боков - рассматриваемым интервалом. Свойства плотности вероятности: 1) Значения функции неотрицательны, т.е. f(x)≥0 2) Основное свойство плотности вероятности: несобственный интеграл от плотности вероятности в пределах от -∞ до +∞ равен единице (геометрически это выражается тем, что площадь фигуры, ограниченной сверху графиком плотности вероятности, снизу - осью OX, равна 1).
Вопрос 25. Дисперсия
Диспе́рсия
случа́йной величины́ —
мера разброса данной случайной
величины,
то есть её отклонения от математического
ожидания.
Обозначается 
в
русской литературе и 
(англ. variance)
в зарубежной. В статистике часто
употребляется обозначение 
или 
.
Квадратный корень из дисперсии, равный 
,
называетсясреднеквадрати́чным
отклоне́нием, станда́ртным
отклоне́нием или
стандартным разбросом. Стандартное
отклонение измеряется в тех же единицах,
что и сама случайная величина, а дисперсия
измеряется в квадратах этой единицы
измерения.
Из неравенства Чебышева следует, что случайная величина удаляется от её математического ожидания на более чем k стандартных отклонений с вероятностью менее 1/k². Так, например, как минимум в 75 % случаев случайная величина удалена от её среднего не более чем на два стандартных отклонения, а в примерно 89 % — не более чем на три.
Определение
Пусть 
—
случайная величина, определённая на
некотором вероятностном
пространстве.
Тогда
где
символ 
обозначает математическое
ожидание[1][2].
[Замечания
Если случайная величина вещественна, то, в силу линейности математического ожидания, справедлива формула:
Дисперсия является вторым центральным моментом случайной величины;
Дисперсия может быть бесконечной. См., например, распределение Коши.
Дисперсия может быть вычислена с помощью производящей функции моментов
:
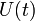Дисперсия целочисленной случайной величины может быть вычислена с помощью производящей функции последовательности.