Вопрос 1 .Правило сложения и умножения

Во многих задачах сложные события, вероятности которых надо найти, удается выразить в виде комбинации других, более простых событий, причем вероятности последних либо заданы, либо непосредственно подсчитываются. В таком случае для решения задач можно использовать формулы, выражающие вероятности суммы и произведения событий через вероятности соответствующих слагаемых и сомножителей.

Правила сложения и умножения вероятностей: если события   попарно несовместны, то справедливо равенство

Из правила сложения вероятностей для двух событий вытекает правило нахождения вероятности противоположного события:

Для произвольных событий A и B имеет место формула:

В случае n слагаемых (n>2) эта формула принимает вид:

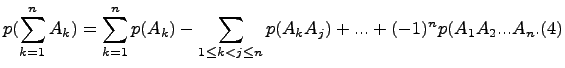
Вероятность p(В|А) события В при условии наступления события А по определению равна:

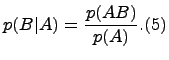
Из этого определения следует формула для вычисления вероятности произведения двух событий:

Для вычисления вероятности произведения n событий (n>2) служит общая формула:

События   называются независимыми в совокупности, если вероятность любого из них не меняется при наступлении какого угодно числа событий из остальных.

Правило умножения вероятностей для n событий: если события   независимы, то вероятность их произведения равна произведению их вероятностей, т.е.

Вычисление вероятности суммы событий можно свести к вычислению вероятности произведения противоположных событий по формуле

В частности, если события   независимы, то

Вопрос 3. Размещения.

Пусть имеется множество из четырех различных цифр {3,5,7,8}. Необходимо составить всевозможные двузначные числа, каждое из которых состоит из различных цифр.Каждое число является упорядоченным подмножеством, состоящим из двух элементов,  данного множества, состоящего из четырех элементов. Перечислим их: 35, 37, 38, 53, 73, 83, 57, 58, 75, 85, 78, 87. Всего таких подмножеств- двузначных чисел получилось 12.  Каждое упорядоченное подмножество называется размещением . Определение : Размещением из п элементов по т называется любое упорядоченное подмножество из т элементов множества, состоящего из п элементов.На практике чаще представляет интерес не конкретный вид размещений, а их количество. Следующая теорема дает общую формулу для вычисления размещений.

 Теорема: Число размещений из n элементов по m равно 

  Доказательство: необходимо заполнить т мест элементами множества из п элементов. Каждое действие- это выбор определенного элемента. Действия совершаются последовательно, значит применимо правило умножения. Первый элемент можно выбрать п способами, второй- (п-1) способами, последний т-ый элемент- (п-(т-1)) способами. Тогда количество размещений равноп(п-1)(п-2)…(п-(т-1)). Умножим и разделим данное выражение на (п-т)!, преобразовав получим более удобный вид :

Пример. Сколько можно составить четырехзначных чисел, состоящих из разных цифр, использую все 10 цифр?

Решение: В числе важен порядок следования цифр. Следовательно, нужно найти количество размещений из 10 по 4: 

  

 Но среди них есть числа с нулем в начале. из полученного значения 5040 необходимо вычесть количество таких чисел. Найдем это количество: т.к. на первом месте стоит о, то оставшиеся три выбираем из 9, т.е. 

  

Искомое количество чисел равно 5040-504=4536.

. Вопрос 2. Перестановки

Рассмотрим случай, когда п=т. Такие размещения называются перестановками.

   Определение: Перестановкой из п элементов называется любое упорядоченное множество , в которое входят по одному разу все п различных элементов данного множества.

Формулу для определения количества перестановок дает теорема.

    Теорема: Число перестановок п различных элементов равно п!, т.е. Р_п=п!

   Доказательство: 

Следовательно, Р_n= n!