
- •Вопрос 20. Электрический ток. Плотность тока. Уравнение непрерывности.
- •Вопрос 21. Закон Ома в интегральной и дифференциальной форме. Сопротивление проводников.
- •Вопрос 22. Тепловое действие тока. Закон Джоуля – Ленца в дифференциальной и интегральной форме.
- •Вопрос 41. Плоская электромагнитная волна. Связь векторов напряженности электрического и магнитного поля.
- •Вопрос 42. Плотность и поток энергии электромагнитного поля.
- •Вопрос 4. Метод векторных диаграмм. Дифракция на круглом отверстии и диске.
- •Вопрос 8. Поляризация при отражении и преломлении света. Закон Брюстера. Двойное лучепреломление.
- •Вопрос 9. Интерференция поляризованного света.
- •1. Электрическое поле в вакууме. Закон Кулона. Закон сохранения заряда. Напряженность электрического поля. Напряженность поля точечного заряда. Принцип суперпозиции. Силовые линии поля.
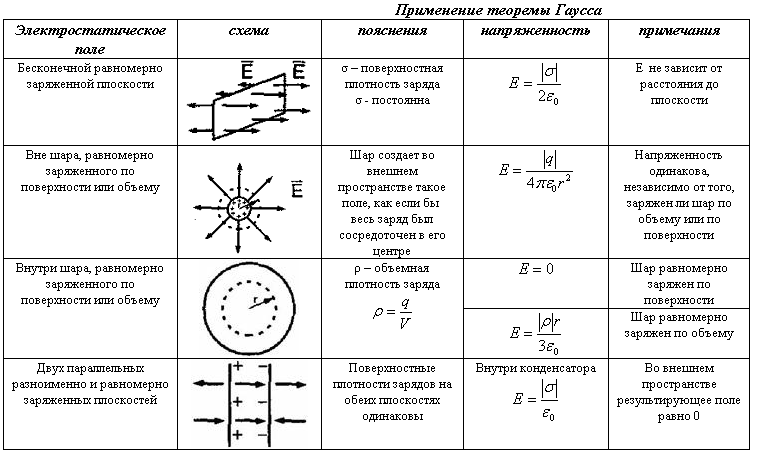
- •Электростатическое поле бесконечной проводящей плоскости
- •5. Электроемкость уединенного проводника. Пример вычисления емкости шарового проводника. Конденсаторы. Емкость конденсатора. Вычисление емкости плоского конденсатора, сферического конденсатора.
- •6. Диполь в однородном электрическом поле. Электрический дипольный момент. Момент сил, действующий на диполь в однородном электрическом поле.
- •8. Энергия системы зарядов. Энергия плоского конденсатора. Энергия электростатического поля. Объемная плотность энергии.
- •12. Магнитное взаимодействие токов. Сила Ампера. Вычисление силы взаимодействия двух прямолинейных проводников с током.
- •13. Действие магнитного поля на движущиеся заряды. Сила Лоренца. Движение заряженных частиц в электрическом и магнитном полях.
- •14. Контур с током в однородном и неоднородном магнитных полях. Магнитный момент контура с током.
- •15. Магнитный поток. Работа при перемещении контура с током в магнитном поле.
- •16. Явление электромагнитной индукции. Закон электромагнитной индукции Фарадея. Правило Ленца. Генератор переменного тока, пример расчета эдс индукции для генератора переменного тока.
- •17. Явление самоиндукции и взаимной индукции. Индуктивность контура. Пример вычисления индуктивности соленоида. Эдс самоиндукции. Токи замыкания и размыкания цепи.
- •18. Природа магнетизма атома. Магнитный момент атома и его механический момент. Гиромагнитное отношение. Момент сил, действующий на атом в магнитном поле.
- •20. Энергия магнитного поля. Плотность энергии магнитного поля.
- •24. Переменный ток. Расчет реактивного сопротивления емкости, индуктивности. Закон Ома для переменного тока.
- •25. Уравнения Максвелла в интегральной и дифференциальной формах, их физический смысл. Вихревое электрическое поле. Ток смещения. Электромагнитное поле.
- •Оптическая разность хода.
- •18.1.2.1. Условия максимума и минимума на разность фаз δ
- •18.1.2.2. Оптическая разность хода
- •18.1.2.3. Условия максимума и минимума на оптическую разность хода
- •30. Интерференция при отражении от тонких пленок. Пример расчета интерференционной картины для плоскопараллельной пластинки.
- •31. Кольца Ньютона. Радиусы темных и светлых колец.
- •32. Дифракция света. Принцип Гюйгенса-Френеля. Метод зон Френеля. Радиусы зон Френеля. Дифракция на круглом отверстии и непрозрачном диске.
- •34. Дифракционная решетка как спектральный прибор. Разрешающая способность дифракционной решетки. Угловая дисперсия.
- •35. Поляризация света. Степень поляризации. Закон Малюса.
- •36. Поляризация света при отражении и преломлении света на границе раздела двух сред.
1. Электрическое поле в вакууме. Закон Кулона. Закон сохранения заряда. Напряженность электрического поля. Напряженность поля точечного заряда. Принцип суперпозиции. Силовые линии поля.
Электрическое поле — особая форма поля, существующая вокруг тел или частиц, обладающих электрическим зарядом, а также в свободном виде в электромагнитных волнах. Электрическое поле непосредственно невидимо, но может наблюдаться по его действию и с помощью приборов. Основным действием электрического поля является ускорение тел или частиц, обладающих электрическим зарядом.
Электрическое поле можно рассматривать как математическую модель, описывающую значение величины напряженности электрического поля в данной точке пространства. Электрическое поле является одной из составляющих единого электромагнитного поля и проявлением электромагнитного взаимодействия.
В настоящее время наука ещё не достигла понимания физической сущности таких полей, как электрическое, магнитное и гравитационное, а также их взаимодействия друг с другом. Пока еще только описаны результаты их механического воздействия на заряженные тела, а также существует теория электромагнитной волны, описываемая Уравнениями Максвелла.
Эффект поля — Эффект поля заключается в том, что при воздействии электрического поля на поверхность электропроводящей среды в её приповерхностном слое изменяется концентрация свободных носителей заряда. Этот эффект лежит в основе работы полевых транзисторов.
Основным действием электрического поля является силовое воздействие на неподвижные (относительно наблюдателя) электрически заряженные тела или частицы. Если заряженное тело фиксировано в пространстве, то оно под действием силы не ускоряется. На движущиеся заряды силовое воздействие оказывает и магнитное поле (вторая составляюшая силы Лоренца).
Зако́н Куло́на — это закон взаимодействия точечных электрических зарядов.
Был открыт Кулоном в 1785 г. Проведя большое количество опытов с металлическими шариками Шарль Кулон дал такую формулировку закона:
Сила взаимодействия двух точечных неподвижных заряженных тел в вакууме прямо пропорциональна произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними.
Важно отметить, что для того, чтобы закон был верен необходимы:
точечность зарядов — то есть расстояние между заряженными телами много больше их размеров.
их неподвижность. Иначе уже надо учитывать возникающее магнитное поле движущегося заряда.
В векторном виде закон записывается следующим образом:
![]()
где
![]() —
сила, с которой заряд 1 действует на
заряд 2; q1,q2 — величина
зарядов;
—
сила, с которой заряд 1 действует на
заряд 2; q1,q2 — величина
зарядов;
![]() —
радиус-вектор (вектор, направленный от
заряда 1 к заряду 2, и равный, по модулю,
расстоянию между зарядами — r12);
k — коэффициент пропорциональности.
—
радиус-вектор (вектор, направленный от
заряда 1 к заряду 2, и равный, по модулю,
расстоянию между зарядами — r12);
k — коэффициент пропорциональности.
В СИ k ≈ 8,987742438·109 Н·м2/Кл2 (или Ф-1·м) и записывается следующим образом:
![]()
Закон сохранения электрического заряда гласит, что алгебраическая сумма зарядов электрически замкнутой системы, сохраняется.
![]()
Требование релятивистской инвариантности приводит к тому, что закон сохранения заряда имеет локальный характер: изменение заряда в любом наперёд заданном объёме равно потоку заряда через его границу.
Напряжённость электри́ческого по́ля— векторная характеристика электрического поля в данной точке, равная отношению силы F, действующей на пробный заряд, помещенный в данную точку поля, к величине этого заряда q:
![]()
Напряжённость электрического поля, векторная физическая величина (Е), являющаяся основной количественной характеристикой электрического поля; определяется отношением силы, действующей со стороны поля на электрический заряд, к величине заряда (при этом заряд должен быть малым, чтобы не изменять ни величины, ни расположения тех зарядов, которые порождают исследуемое поле). В вакууме Н. э. п. удовлетворяет принципу суперпозиции, согласно которому полная напряжённость поля в точке равна геометрической сумме напряжённостей полей, создаваемых отдельными заряженными частицами. Для электростатического поля Н. э. п. может быть представлена как градиент электрического потенциала ; Е = — grad. В Международной системе единиц (СИ) Н. э. п. измеряется в единицах в/м.
Принцип суперпозиции — один из самых общих законов во многих разделах физики. В самой простой формулировке принцип суперпозиции гласит:
результат воздействия на частицу нескольких внешних сил есть просто сумма результатов воздействия каждой их сил.
Наиболее известен принцип суперпозиции в электростатике, в которой он утверждает, что электростатический потенциал, создаваемый в данной точке системой зарядов, есть сумма потенциалов отдельных зарядов.
Принцип суперпозиции может принимать и иные формулировки, которые, подчеркнём, полностью эквивалентны приведённой выше:
Взаимодействие между двумя частицами не изменяется при внесении третьей частицы, также взаимодействующей с первыми двумя;
Энергия взаимодействия всех частиц в многочастичной системе есть просто сумма энергий парных взаимодействий между всеми возможными парами частиц. В системе нет многочастичных взаимодействий.
2. Поток вектора напряженности электростатического поля. Теорема Гаусса и ее применение к расчету напряженности полей. Поле бесконечной равномерно заряженной плоскости. Поле заряженной сферы и заряженного шара. Поле бесконечной равномерно заряженной нити. Дифференциальная форма теоремы Гаусса.
Поток
векторного
поля - поток Φ векторного
поля
![]() через
поверхность
S - интеграл по поверхности
через
поверхность
S - интеграл по поверхности
![]() ,
,
при этом векторный элемент площади поверхности определяется как
![]() ,
,
где
![]() -
единичный
вектор, нормальный к поверхности.
-
единичный
вектор, нормальный к поверхности.
Теорема Гаусса
Поток вектора напряжённости электрического поля через любую, произвольно выбранную, замкнутую поверхность равен алгебраической сумме заключённых в этой поверхности электрических зарядов, делённой на электрическую постоянная ε0 :
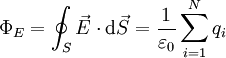 .
.
Данное выражение представляет собой теорему Гаусса в интегральной форме. В дифференциальной форме теорема Гаусса выражается следующим образом:
![]() ,
,
где ρ — объёмная плотность заряда
![]() .
.
Теорема Гаусса выражает связь между потоком напряженности электрического поля сквозь замкнутую поверхность и зарядом в объёме, ограниченной этой поверхностью. Физической основой теоремы Гаусса является закон Кулона или, иначе, теорема Гаусса является интегральной формулировкой закона Кулона.
3. Работа сил электростатического поля при перемещении зарядов. Потенциальный характер электростатического поля. Циркуляция вектора напряженности электростатического поля. Потенциал электростатического поля. Потенциал поля точечного заряда. Связь между напряженностью и потенциалом. Эквипотенциальные поверхности.
Работа электростатического поля (A)
A = Fd=qEd,
|
|
A1 = Fd1 cos , но d1 cos = d, A1 = qEd
A = A1
A1,2,3,1 = A1,2 + A2,3 + A3,1
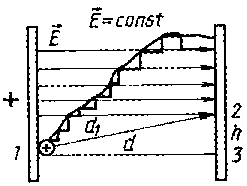
A1,2,3,1 = qEd1 cos a + Eqh cos 90° + Eqd cos 180° = qEd + 0 + ( - qEd)
A1,2,3,1 =0
т. е. работа при перемещении заряда между двумя точками в электростатическом поле не зависит от формы траектории, а зависит от положения этих точек.
Работа по замкнутой траектории равна нулю.
Электростатическое поле, как и гравитационное, потенциальное.
Электростатические силы, как и гравитационные, относятся к консервативным (потенциальным) силам. Работа консервативных сил равна изменению потенциальной энергии взятому с противоположным знаком.
A = Ai = (W2 W1) = Wп
A = Wп |
Потенциальная энергия W заряда q в однородном электростатическом поле напряженностью E на расстоянии d от 0 потенциального уровня
Wп = Eqd
Потенциальность электростатического поля. Электрический потенциал
Р абота
поля по переносу пробного q
заряда из некоторой точки 1 в некоторую
точку 2 не зависит от траектории его
движения и определяется для данного
поля и данного заряда только координатами
этих точек. Для случая, когда источником
поля является точечный заряд Q (рис.
1.6.1) это нетрудно обосновать следующим
образом. Работа на элементарном отрезке
траектории, по известному из механики
определению, есть:
абота
поля по переносу пробного q
заряда из некоторой точки 1 в некоторую
точку 2 не зависит от траектории его
движения и определяется для данного
поля и данного заряда только координатами
этих точек. Для случая, когда источником
поля является точечный заряд Q (рис.
1.6.1) это нетрудно обосновать следующим
образом. Работа на элементарном отрезке
траектории, по известному из механики
определению, есть:
![]() .
Раскрывая скалярное произведение
векторов через угол
между ними, получаем
.
Раскрывая скалярное произведение
векторов через угол
между ними, получаем
 .
(1.6.1)
.
(1.6.1)
Суммируя (интегрируя) все элементарные работы, находим
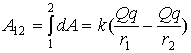 ,
(1.6.2)
,
(1.6.2)
что и требовалось доказать. Работа определяется только расстояниями от источника до начальной и конечной точки траектории. Такое силовое поле в механике мы называли потенциальным.
Из принципа суперпозиции следует потенциальность электростатического поля, созданного любой системой зарядов. Из (1.6.2) и принципа суперпозиции следует также, что работа электростатических сил над зарядом, перемещаемым по замкнутому контуру, равна 0:
![]() .
(1.6.3)
.
(1.6.3)
Таким
образом, для любого контура в
электростатическом поле циркуляция
напряженности – тождественный
нуль. В соответствии с утверждением
(1.5.6) напряженность электростатического
поля (с точностью до знака) может быть
истолкована как градиент некоторой
функции координат, называемой потенциалом
электростатического поля
![]() :
:
![]() .
(1.6.4)
.
(1.6.4)
Используя определение напряженности электростатического поля и формулу связи между силой F и потенциальной энергией W, известную из курса механики
![]() ,
(1.6.5)
,
(1.6.5)
из (1.6.4) получим, что потенциал поля в данной точке наблюдения численно равен потенциальной энергии пробного заряда q, помещаемого в данную точку, отнесенной к величине этого заряда:
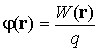 .
.
Иначе говоря, поле, работа которого при перемещении заряда по любой замкнутой траектории равна нулю, называют потенциальным. Пример потенциального поля — электростатическое поле.
Потенциал
В качестве энергетической характеристики поля в данной точке используют потенциал
Потенциал электростатического поля — отношение потенциальной энергии заряда в поле к этому заряду:
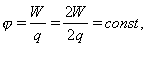
Выражается потенциал в вольтах:
![]()
Потенциал не зависит от заряда q, помещенного в данную точку поля.
Для однородного поля
![]()
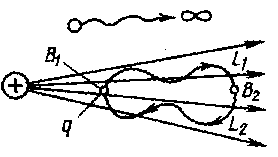
потенциал зависит от напряженности E и от расстояния d от данной точки поля до нулевого потенциального уровня.
Работа поля по перемещению единичного положительного заряда из данной точки электрического поля в бесконечность характеризует потенциал в данной точке поля созданного точечным зарядом Q смотри рисунок выше,
![]()
где Q — заряд создающий поле, R — расстояние от данной точки поля до заряда Q.
Потенциальная энергия электрического взаимодействия системы n точечных зарядов qi равна
Wп = 1/2qi i
здесь i — потенциал поля в точке, где находится заряд qi
Если поле создано двумя зарядами, то выполняется следствие принципа суперпозиции полей.
= 1 + 2
Потенциал поля, созданного несколькими заряженными телами, равен алгебраической сумме потенциалов отдельных полей, создаваемых в данной точке пространства каждым из заряженных тел:
= 1 + 2 n
Эквипотенциальные поверхности
Поверхность, все точки которой имеют одинаковый потенциал, называют эквипотенциальной.
A = FS cos |
если = 90 , то A = 0
1 = 2 = 3 = 4
Силовые линии перпендикулярны такой поверхности .
4. Проводники в электростатическом поле. Явление электростатической индукции. Свойства индукционных зарядов, характер их распределения. Напряженность поля вблизи поверхности проводника. Поле внутри проводника. Потенциал проводника.
Проводники в электростатическом поле
Проводниками называют вещества, в которых есть свободные носители зарядов. Например, в металлах ими являются свободные электроны. В отсутствие поля свободные электроны совершающие тепловые движения. Под действием электрического поля свободные электроны металлической пластины начинает перемещаться против линии напряженности электрического поля.
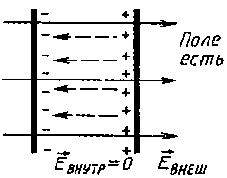 Левая
часть пластины заряжается отрицательно,
а правая положительно. В этом состоит
явление электростатической индукции.
Электроны перемещаются за ничтожно
малое время до тех пор пока напряженность
результирующего поля внутри пластины
не станет равным нулю. Электростатическое
поле внутри проводника равно 0, так как
Eвнутр и Eвнешн
равны по модулю, но противоположно
направлены (см. рис. слева, E = 0).
На этом основана электростатическая
защита (М. Фарадей, 1937)
Левая
часть пластины заряжается отрицательно,
а правая положительно. В этом состоит
явление электростатической индукции.
Электроны перемещаются за ничтожно
малое время до тех пор пока напряженность
результирующего поля внутри пластины
не станет равным нулю. Электростатическое
поле внутри проводника равно 0, так как
Eвнутр и Eвнешн
равны по модулю, но противоположно
направлены (см. рис. слева, E = 0).
На этом основана электростатическая
защита (М. Фарадей, 1937)
Радиоприемники в автомашинах находятся в металлических корпусах; металлические колпачки на электровакуумных лампах...
Э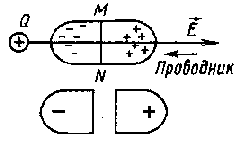 лектростатическая
индукция
лектростатическая
индукция
Если разделить пластину пополам вдоль линии MN, то обе половины окажутся заряженными разноименными зарядами (см. рис. Справа)
