Вопрос 8. Поляризация при отражении и преломлении света. Закон Брюстера. Двойное лучепреломление.

Поляризованный свет можно получить, используя отражение или преломление света от диэлектрических изотропных сред (например, от стекла). Если угол падения света на границу раздела двух диэлектриков отличен от нуля, отраженный и преломленный лучи оказываются частично поляризованными. В отраженном луче преобладают колебания, перпендикулярные плоскости падения (на рис. 5.9 эти колебания обозначены точками), в преломленном луче – колебания, параллельные плоскости падения (на рис. 5.9 они изображены двусторонними стрелками).

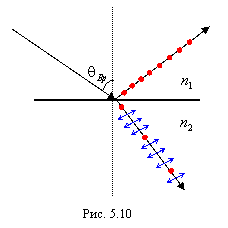
Степень поляризации того и другого луча зависит от угла падения луча. У каждой пары прозрачных сред существует такой угол падения, при котором отраженный свет становится полностью плоскополяризованным, а преломленный луч остается частично поляризованным, но степень его поляризации при этом угле максимальна (рис. 5.10). Этот угол называется углом Бpюстеpа. Угол Брюстера определяется из

Закона Брюстера:  , где n₂₁ — показатель преломления второй среды относительно первой, θ_Br — угол падения (угол Брюстера). Закон Брюстера — закон оптики, выражающий связь показателя преломления с таким углом, при котором свет, отражённый от границы раздела, будет полностью поляризованным в плоскости, перпендикулярной плоскости падения, а преломлённый луч частично поляризуется в плоскости падения, причем поляризация преломленного луча достигает наибольшего значения. Легко установить, что в этом случае отраженный и преломленный лучи взаимно перпендикулярны. Можно показать, что при падении

волны под углом Брюстера отраженный и преломленный лучи взаимно перпендикулярны.

Таким образом, пластинка диэлектрика сортирует лучи естественного света, отражая преимущественно лучи с одним направлением колебаний и пропуская перпендикулярные колебания

 

 

Поляроид — название синтетической пластиковой плёнки, используемой для поляризации света. Обычный свет превращается в плоскополяризированный, проходя через пластинки, сделанные из материала, называемого поляроидом, или через кристаллы кальцита (особая кристаллическая форма CaCO_3.

Вопрос 9. Интерференция поляризованного света.

Явления интерференции поляризованных лучей исследовались в классических опытах Френеля и Арго (1816 г.), доказавших поперечность световых колебаний. Суть их в зависимости результата интерференции от угла между плоскостями световых колебаний: полосы наиболее контрастны при параллельных плоскостях и исчезают, если волны поляризованы ортогонально. Трудность получения интерференции поляризованных волн состоит в том, что при наложении двух когерентных лучей, поляризованных во взаимно перпендикулярных направлениях, никакой интерференционной картины с максимумами и минимумами интенсивности получиться не может. Интерференция возникает только в том случае, если колебания во взаимодействующих лучах совершаются вдоль одного и того же направления. Колебания в двух лучах, первоначально поляризованных во взаимно перпендикулярных направлениях, можно свести в одну плоскость, пропустив эти лучи через поляризующую кристаллическую пластинку.

Рассмотрим схему получения интерференции поляризованных лучей (рис. 11.13).

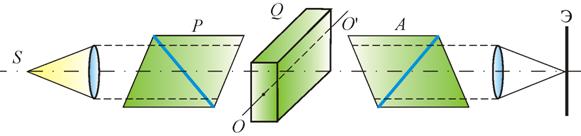
Рис. 11.13

Прошедшее через поляризатор Р излучение точечного источника S попадает на полуволновую кристаллическую пластинку Q, которая позволяет изменять угол между плоскостями поляризации интерферирующих лучей: ее поворот на угол α поворачивает вектор   на 2α. Если наблюдать интерференционные полосы через анализатор А, то при его повороте на π/2 картина, наблюдаемая на экране Э, инвертируется: из-за дополнительной разности фаз π темные полосы становятся светлыми и наоборот. Анализатор здесь необходим также для того, чтобы свести колебания двух различно поляризованных лучей в одну плоскость.

при прохождении поляризованного света через кристаллическую пластинку разность хода между двумя компонентами поляризации зависит от толщины пластинки, среднего угла преломления и разности показателей   и   . Очевидно, что возникающая при этом разность фаз

(11.5.1)

различна для разных длин волн, и тем самым интерференционная картина оказывается окрашенной. Для плоскопараллельных пластинок наблюдаются полосы равного наклона, а для тонких клиновидных пластинок - полосы равной толщины.

Приведенная формула позволяет для любой фазовой пластинки рассчитать интенсивность на выходе при скрещенных поляризаторе и анализаторе:

.

(11.5.2)