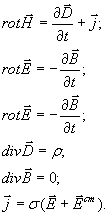Вопрос 22. Тепловое действие тока. Закон Джоуля – Ленца в дифференциальной и интегральной форме.

Если в проводнике течет постоянный ток и проводник остается неподвижным, то работа сторонних сил расходуется на его нагревание. Опыт показывает, что в любом проводнике происходит выделение теплоты, равное работе, совершаемой электрическими силами по переносу заряда вдоль проводника. Если на концах участка проводника имеется разность потенциалов   , тогда работу по переносу заряда q на этом участке равна 

По определению I= q/t. откуда q= I t. Следовательно 

Так как работа идет па нагревание проводника, то выделяющаяся в проводнике теплота Q равна работе электростатических сил

(17.13)

Соотношение (17.13) выражает закон Джоуля-Ленца в интегральной форме. Введем плотность тепловой мощности   , равную энергии выделенной за единицу время прохождения тока в каждой единице объема проводника

где S - поперечное сечение проводника,   - его длина. Используя (1.13) и соотношение   , получим

Но   - плотность тока, а   , тогда

с учетом закона Ома в дифференциальной форме   , окончательно получаем

(17.14)

Формула (17.14) выражает закон Джоуля-Ленца в дифференциальной форме: объемная плотность тепловой мощности тока в проводнике равна произведению его удельной электрической проводимости на квадрат напряженности электрического поля.

Вопрос 41. Плоская электромагнитная волна. Связь векторов напряженности электрического и магнитного поля.

Понятие электромагнитной волны.

Как известно¹, электромагнитные поля определяются путём задания в каждой точке пространства четырёх векторов:

а) вектора напряжённости электрического поля  ;

б) вектора напряжённости магнитного поля  ;

в) вектора электрического смещения  ;

г) вектора магнитной индукции  .

Эти векторы не являются независимыми. Попарно векторы , а также   связаны друг с другом с помощью материальных уравнений. Наиболее простой вид материальные уравнения имеют для однородных изотропных сред, относительные значения диэлектрической  и магнитной  проницаемостей которых имеют постоянные значения для любой точки наблюдения электромагнитного поля:

(1.1a)

Вектора   в общем случае зависят как от координат точки наблюдения   так и от времени   и могут быть найдены из системы уравнений Максвелла, решениями которой они являются:

(1.1b)

В этих уравнениях:  - коэффициент удельной электропроводности среды, в которой рассматривается электромагнитное поле,   - напряженность электрического поля сторонних источников ,  - объемная плотность сторонних электрических зарядов;  - плотность токов проводимости.

В дальнейшем будем называть сторонними токами, такие токи, которые вызываются электрическими полями   сторонних источников, причём, их плотность  может быть вычислена по формуле:  .

Отметим, что для полей независящих от времени  . В этом случае система (1.1b) распадается на две независимые системы: а) систему уравнений электростатики, определяющую постоянные во времени поля  , и б) систему уравнений магнитостатики, определяющую постоянные во времени поля .

Для электромагнитных полей, зависящих от времени из системы уравнений Максвелла (1.1b) следует взаимосвязь изменения их электрических и магнитных полей . Наиболее просто в этом убедиться, если рассматривать зависящее от времени электромагнитное поле в среде, в которой нет сторонних зарядов, сторонних токов , плотность которых может быть вычислена по формуле  , и отсутствует проводимость ( ) .

Таким условиям соответствует электромагнитное поле в вакууме, в котором отсутствуют источники сторонних токов и зарядов. Очень близкими свойствами обладает сухой воздух, проводимостью которого в обычных условиях можно пренебречь.

В этом случае первые два уравнения системы (1.1a) связывают между собой изменение в пространстве и времени электрического и магнитного полей. Отсюда следует основное свойство зависящих от времени электромагнитных полей, состоящее в согласованности изменения электрического и магнитного поля.

Так, при изменении во времени электрического поля возникает изменяющееся в пространстве переменное магнитное поле, которое приводит к появлению меняющегося в пространстве электрического поля. И, наоборот, при изменении во времени магнитного поля возникает изменяющееся в пространстве переменное электрическое поле, которое приводит к появлению меняющегося в пространстве магнитного поля.

Физическая причина такой взаимосвязи является следствием закона электромагнитной индукции и наличием тока смещения, связывающих между собой электрическое и магнитное поля. Причём, взаимосвязь электрических и магнитных полей имеет место даже в отсутствии сторонних токов и зарядов, являющихся источниками электромагнитного поля.

Процесс согласованного изменения электрического и магнитного полей в пространстве и времени, при распространении электромагнитного возмущения из одной точки пространства в другую, получил название электромагнитной волны.

Источниками электромагнитных волн, как это следует из системы уравнений Максвелла (1.1b), являются меняющиеся во времени сторонние токи и заряды. Исследование процесса излучения электромагнитных полей меняющимися во времени сторонними токами и зарядами будет более рассмотрено подробно в главе 2.

Существование электромагнитных волн впервые было предсказано английским физиком М.Ф. Фарадеем в 1832г. В 1865г. английский физик Дж. К. Максвелл теоретически показал, что скорость распространения электромагнитных волн в вакууме равна скорости света. Подтверждение открытых свойств электромагнитных волн и обширные их экспериментальные исследования было сделано немецким физиком Г. Герцем (1887-1888).

В ходе экспериментальных исследований свойств электромагнитных волн Г. Герц обнаружил, что законы распространения электромагнитных волн и света одинаковы. В частности, у них одинаковый характер преломления и отражения от диэлектрических и металлических тел. Часть из этих опытов мы изложим в дальнейшем по мере более детального изучения электромагнитных волн и оптики.