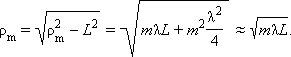31. Кольца Ньютона. Радиусы темных и светлых колец.

Кольца Ньютона — кольцеобразные интерференционные максимумы и минимумы, появляющиеся вокруг точки касания слегка изогнутой выпуклой линзы и плоскопараллельной пластины. Интерференция возникает в воздушном зазоре между линзой и пластиной (отраженный свет).

Они наблюдаются при отражении света от соприкасающихся друг с другом плоскопараллельный толстой стеклянной пла­стинки и плоско-выпуклой линзы с большим радиусом кривизны (рис. 52). Роль тонкой пленки, от поверхно­стей которой отражаются когерентные волны, играет воздушный зазор между пластинкой и линзой (вслед­ствие большой толщины пластинки и линзы за счет от­ражений от других поверхностей интерференционные полосы не возникают). При нормальном падении света полосы равной толщины имеют вид концентрических окружностей, при наклонном падении — эллипсов. Най­дем радиусы колец Ньютона, получающихся при паде­нии света по нормали к пластинке. В этом случае cos i₂ ~ 1 и оптическая разность хода равна удвоенной толщине зазора [см. формулу ; предполагается, что в зазоре п = 1]. Как следует из рис. 52:

где R — радиус кривизны линзы, r — радиус окружно­сти, всем точкам. которой соответствует одинаковый за­зор b. Ввиду малости b мы пренебрегли величиной Ь² по сравнению с 2Rb.

В соответствии с (19.11) b = r²/2R. Чтобы учесть возникающее при отражении от пластинки изменение фазы на , нужно при вычислении к 2Ь = r²/R приба­вить /2. В результате получится:

В точках, для которых возникнут максимумы; в точках, для которых ,— минимумы интенсивности. Оба усло­вия можно объединить в одно:

причем четным значениям m будут соответствовать мак­симумы, а нечетным — минимумы интенсивности.

Подставив сюда выражение (19.12) для и разре­шив получающееся уравнение относительно r, найдем радиусы светлых и темных колец Ньютона:

(m = 1, 2, 3…)

четным m соответствуют радиусы светлых колец, не­четным m — радиусы темных колец. Значению m = 1 соответствует r = 0, т. е. точка в месте касания пла­стинки и линзы. В этой точке наблюдается минимум ин­тенсивности, обусловленный изменением фазы на при отражении световой волны от пластинки.

32. Дифракция света. Принцип Гюйгенса-Френеля. Метод зон Френеля. Радиусы зон Френеля. Дифракция на круглом отверстии и непрозрачном диске.

Дифракцией света называется явление отклонения света от прямолинейного направления распространения при прохождении вблизи препятствий (более широком смысле - любые отклонения при распространении волн от законов геометрической оптики ).

Дифракционная картина – система чередующихся светлых и темных колец. Если препятствие имеет линейный характер (щель, нить, край экрана), то на экране возникает система параллельных дифракционных полос.

Френель развил количественную теорию дифракционных явлений . В основу теории Френель положил принцип Гюйгенса, дополнив его идеей об интерференции вторичных волн.

Р исунок ниже иллюстрирует принцип Гюйгенса–Френеля.

Пусть поверхность S представляет собой положение волнового фронта в некоторый момент. Для того чтобы определить колебания в некоторой точке P, вызванное волной, по Френелю нужно сначала определить колебания, вызываемые в этой точке отдельными вторичными волнами, приходящими в нее от всех элементов поверхности S (ΔS₁, ΔS₂ и т. д.), и затем сложить эти колебания с учетом их амплитуд и фаз. При этом следует учитывать только те элементы волновой поверхности S, которые не загораживаются каким-либо препятствием.

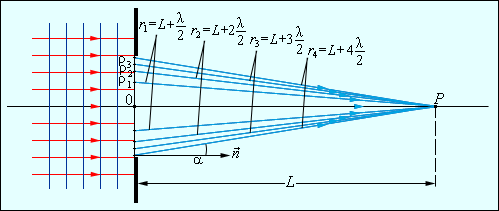
Рассмотрим в качестве примера простую дифракционную задачу о прохождении плоской монохроматической волны от удаленного источника через небольшое круглое отверстие радиуса R в непрозрачном экране :

Точка наблюдения P находится на оси симметрии на расстоянии L от экрана. В соответствии с принципом Гюйгенса–Френеля следует мысленно заселить волновую поверхность, совпадающую с плоскостью отверстия, вторичными источниками, волны от которых достигают точки P. В результате интерференции вторичных волн в точке P возникает некоторое результирующее колебание, квадрат амплитуды которого (интенсивность) нужно определить при заданных значениях длины волны λ, амплитуды A₀ падающей волны и геометрии задачи. Для облегчения расчета Френель предложил разбить волновую поверхность падающей волны в месте расположения препятствия на кольцевые зоны (зоны Френеля) по следующему правилу: расстояние от границ соседних зон до точки P должны отличается на полдлины волны, то есть

 

Е сли смотреть на волновую поверхность из точки P, то границы зон Френеля будут представлять собой концентрические окружности (рис. ниже).

3

Из рис. Выше легко найти радиусы ρ_m зон Френеля:

 

Так в оптике λ << L, вторым членом под корнем можно пренебречь. Количество зон Френеля, укладывающихся на отверстии, определяется его радиусом R:

 

Здесь m – не обязательно целое число. Результат интерференции вторичных волн в точке P зависит от числа m открытых зон Френеля. Легко показать, что все зоны имеют одинаковую площадь:

33. Дифракция Фраунгофера на щели. Распределение интенсивности света в дифракционной картине. Условия максимумов и минимумов интенсивности. Дифракционная решетка. Дифракция Фраунгофера на решетке. Условия максимумов и минимумов интенсивности.

Дифракцией называется совокупность явлений, на­блюдаемых при распространении света в среде с резкими неоднородностями и связанных с отклонениями от за­конов геометрической оптики. Дифракция, в частности, приводит к огибанию световыми волнами препятствий и проникновению света в область геометрической тени.Различают два случая дифракции. Если источник света и точка наблюдения Р расположены от препят­ствия настолько далеко, что лучи, падающие на препят­ствие, и лучи, идущие в точку Р, образуют практически параллельные пучки, говорят о дифракции Фраунгофера или о д ифракции в параллельных лучах. В противном случае говорят о дифракции Френеля. Дифракцию Фраунгофера можно наблю­дать, поместив за источником света S и перед точкой наблюдения Р по линзе так, чтобы точки S и Р оказа­лись в фокальной плоскости соответствующей линзы (см рис.).

Р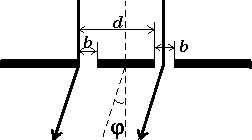 ассмотрим экран с двумя щелями, на которые нормально падает плоская монохроматическая волна. Расчеты показывают, что интенсивность света за экраном будет зависеть от угла   между направлением распространения света и п ерпендикуляром к экрану :

 

где I₀ - интенсивность света в центре дифракционной картины, когда открыта только одна щель, b - ширина щели, d - расстояние между щелями, k=2 / - волновое число,  - длина волны света,  - дополнительная разность хода между интерферирующими лучами (в случае наклонного падения плоской волны на экран или когда одна из щелей закрыта стеклянной пластинкой). Первый сомножитель в квадратных скобках описывает дифракцию Фраунгофера на одной щели, а второй сомножитель - интерференцию от двух точечных источников. Общая энергия, проходящая через одну щель, пропорциональна b, а ширина дифракционной картины пропорциональна 1/b. Поэтому, интенсивность света I₀ в центре дифракционной картины будет пропорциональна b². Если мы рассмотрим дифракцию на двух щелях, то в пределах первого дифракционного максимума мы можем наблюдать N интерференционных полос, где N=2d/b.

Приведённый ниже рисунок показывает зависимость интенсивности света от угла  в случае д ифракции на одной щели (кривая красного цвета) и в случае дифракции на двух щелях  (кривая синего цвета). Из рисунка видно, что в случае дифракции на двух щелях, огибающая интенсивности интерференционных полос повторяет кривую дифракции на одной щели.

Говоря о дифракции Фраунгофера, мы подразумеваем случай, когда наблюдение дифракционной картины производится на достаточно большом расстоянии от экрана с щелями. Количественный критерий дифракции Фраунгофера описывается следующей формулой:

z >> d²/

где z - расстояние от экрана с щелями до точки наблюдения. В непосредственной близости к щелям дифракционная картина будет описываться формулами.

Условия max и min смотри в билете 31