Оптическая разность хода.

Вместо разности фаз интерферирующих волн удобно ввести в рассмотрение пропорциональную ей величину - оптическую разность хода, которая отличается множителем , где - длина световой волны.

Изменению разности фаз на соответствует изменение разности хода на .

В вакууме оптическая разность хода в отличие от разности фаз имеет наглядную и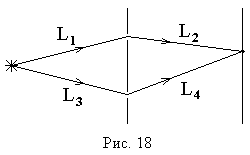 нтерпретацию. Если две интерферирующие волны испускаются одним источником света, то разность хода - это геометрическая разность длин путей, по которым два интерферирующих луча от одной точки источника достигли одной точки экрана.

Например, в оптической схеме опыта Юнга, изображенной на рис. 18, разность хода для точки P на экране находится по формуле:

.

В изотропной среде скорость света в n раз меньше, чем в вакууме, здесь n - показатель преломления среды. Частота света в среде и в вакууме одинакова, поэтому длина волны в среде в n раз меньше. В соответствии с соотношением вместо реального уменьшения длины волны можно рассматривать неизменную и соответствующее увеличение длины пути луча. С этой целью вводится понятие оптической длины пути, которая в n раз больше геометрической длины. Далее, употребляя термин "разность хода", всегда будем иметь в виду оптическую разность хода.

Заменяя разность фаз интерферирующих волн оптической разностью хода, получаем следующее выражение для интенсивности интерференционной картины:

.

Приемники света в оптическом диапазоне реагируют на интенсивность света, а не на напряженность электрического или магнитного полей. Поэтому измеряемые в опыте величины, ширина полос и видность, также могут быть выражены через интенсивность, а значит и через оптическую разность хода. Следовательно, понятие оптической разности хода позволяет свести оптическую задачу по интерференции к геометрической задаче отыскания разности хода.

Отметим, что разность хода лучей можно отсчитывать не только как разность длин путей от источника до точки наблюдения, но и как разность длин путей от двух точек любой поверхности равной фазы волны до точки наблюдения. При этом, конечно, две точки на поверхности равной фазы - не произвольные точки, а должны быть точками, через которые реально проходят лучи, попадающие в точку наблюдения. Так на рис. 18 , поэтому две щели находятся на поверхности равной фазы, и, следовательно, разность хода можно найти по упрощенной формуле . Этот прием часто используется при решении задач.

18.1.2.1. Условия максимума и минимума на разность фаз δ

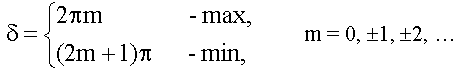
18.1.2.2. Оптическая разность хода

Пусть для простоты, начальные фазы α₁ и α₂ интерферирующих волн равны нулю, тогда:

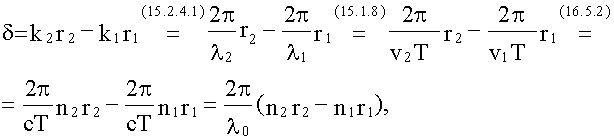
здесь λ₀ = cT - длина световой волны в вакууме.

Оптической разностью хода называют величину:

.

Тогда:

.

18.1.2.3. Условия максимума и минимума на оптическую разность хода

Из (18.1.2.1.) и (18.1.2.2.):

П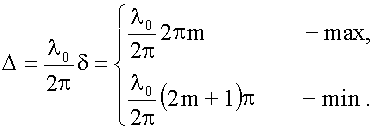 осле сокращения получим условия на Δ:

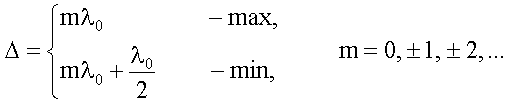
30. Интерференция при отражении от тонких пленок. Пример расчета интерференционной картины для плоскопараллельной пластинки.

Интерференция - физическое явление, наблюдаемое при сложении волн (световых, звуковых и т. п.), усиление волн в одних точках пространства и ослабление в других (или сложение двух или более волн, при котором амплитуда результирующей волны зависит от разности фаз исходных волн в данной точке пространства)

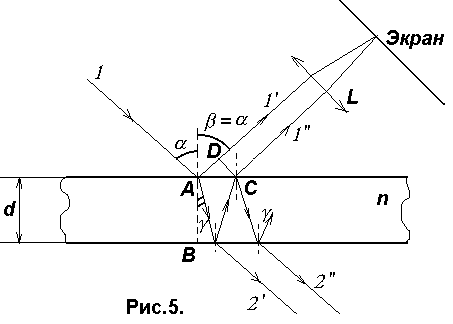
Пусть на плоскопараллельную прозрачную пленку (пластинку) с показателем преломления n и толщиной d под углом  падает плоская монохроматическая волна (для простоты рассмотрим один луч).

На поверхности пленки в точке А волна частично отражается (луч 1- ) и частично преломляется (луч АВ). В точке В волна также частично отражается (луч ВС) и частично преломляется (луч 2- ). То же самое происходит в точке С.

Причем преломленная волна (луч 1" ) накладывается на волну непосредственно отраженную от верхней поверхности (луч 1- ). Эти две волны когерентны, если оптическая разность хода меньше длины когерентности l_ког, и в этом случае они интерферируют.

Оптическая разность хода двух волн =(AB+BC)n-(AD-/2),

где /2 - потеря полуволны при отражении луча 1- в точке А. Используя закон преломления n₁sin = n₂sin и учитывая, что в рассматриваемом случае n₁=1, n₂=n, можно показать, что .(17)

В точке наблюдения на экране будет максимум, если m и минимум, если (2m+1)/2[см.(15),(16)].

Возможность уменьшения вредного отражения света вследствие интерференции в тонких пленках широко используется в современных оптических приборах. Для этого на передние поверхности линз, призм наносят тонкие пленки с показателем преломления n= и толщиной d, которая определяется из условия минимума при интерференции волн, отраженных от границ раздела сред с n₁ и n и n и n₂

 2dn=(2m+1)/2, m=0,1,2-(18)

Минимальная толщина пленки соответствует m=0

d=/(4n)

Такая оптика получила название просветленной оптики.