5.2. Представление графов

Важным вопросом, особенно для приложений теории графов, является определение возможных способов представления графов. Самый простой способ - полное перечисление множеств VиЕ.Однако, очевидно, что в этом случае выявление у графа различных характеристик и свойств будет крайне затруднительным. Граф можно представить в виде некоторого графического изображения и визуально определить некоторые свойства и характеристики заданного графа. Однако, при наличии в графе'большого числа ребер и вершин этот способ также мало пригоден. Рассматривая различные возможные способы представления графов, мы должны иметь в виду потребность ввода соответствующей информации в компьютер. В этой связи ввод информации в числовом виде предпочтителен, хотя современные технические средства допускают ввод и графической информации (таблиц, текста, графиков, рисунков и т.д.), после чего может производиться обработка такой информации.

Матрица смежности.Если вершины графаGпомечены меткамиv1, v2,..., vn,то элементы матрицы смежностиA(G)размераV, xV определяются следующим образом:A(i.j) =1, еслиviсмежна сvj; A(ij)= 0 в противном случае (рис. 1.9,а).

Матрица инцидентности.Если вершины графаGпомечены меткамиv1, v2,..., vm, а ребра - меткамие1, е2,..., еп,то элементы матрицы инцидентностиI(G)размераМхNопределяются правилом:B(ij) =1, еслиviинцидентнаej; B(iJ)= 0 в противном случае (см. рис. 1.9,б).

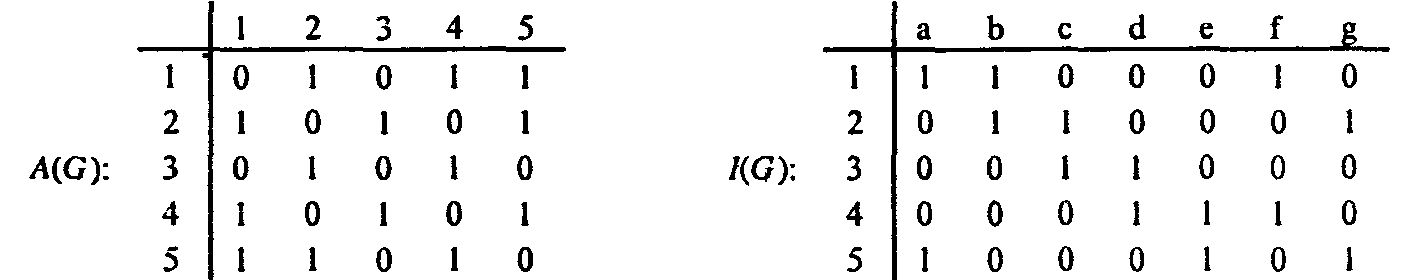
Рис. 1.9, а.Матрица смежностиРис. 1.9, б.Матрица инцидентности

Для ориентированного графа G,имеющегоN вершин можно рассмотреть матрицудостижимостиC(G)размераN х N,элементы которой определяются так: С(I,J)= 1, если вершинаvjдостижима изvi; C(I, J)= 0 в противном случае. Ниже приведен пример ориентированного графа и его матрицы достижимости, рис. 1.10.

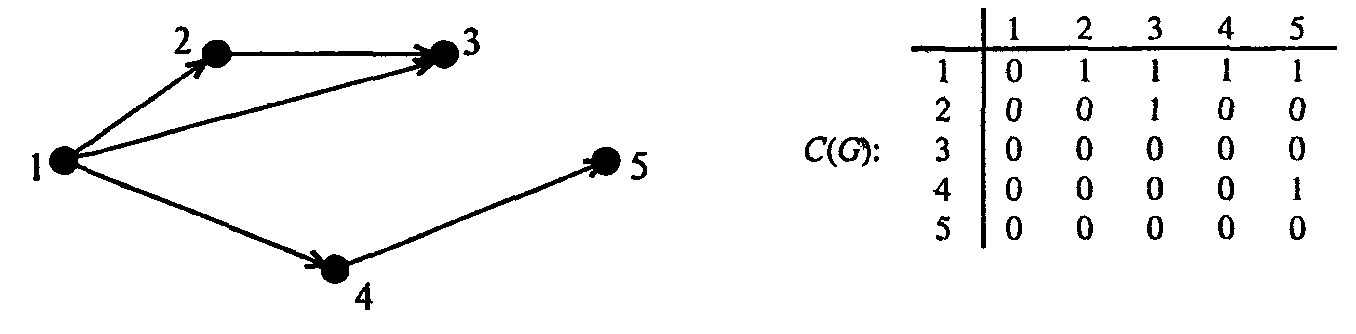
Рис. 1.10.Матрица достижимости ориентированного графа

Контрольные вопросы

1. Каким образом определяется граф?

2. Что является путем в графе?

3. Как определяется такой вид графа, как дерево?

4. Какими способами можно задать граф?

§ 6. Алгоритм и его свойства

6.1. Различные подходы к понятию «алгоритм»

Понятие алгоритма - одно из фундаментальных понятий информатики. Алгоритмизация наряду с моделированием выступает в качестве общего метода информатики. К реализации определенных алгоритмов сводятся процессы управления в различных системах, что делает понятие алгоритма близким и кибернетике.

Алгоритмы являются объектом систематического исследования пограничной между математикой и информатикой научной дисциплины, примыкающей к математической логике - теории алгоритмов.

Особенность положения состоит в том, что при решении практических задач, предполагающих разработку алгоритмов для реализации на ЭВМ, и тем более при использовании на практике информационных технологий, можно, как правило, не опираться на высокую формализацию данного понятия. Поэтому представляется целесообразным познакомиться с алгоритмами и алгоритмизацией на основе содержательного толкования сущности понятия алгоритма и рассмотрения основных его свойств. При таком подходе алгоритмизация более выступает как набор определенных практических приемов, особых специфических навыков рационального мышления в рамках заданных языковых средств. Можно провести аналогию между этим обстоятельством и рассмотренным выше подходом к измерению информации: тонкие математические построения при «кибернетическом» подходе не очень нужны при использовании гораздо более простого «объемного» подхода при практической работе с компьютером.

Само слово «алгоритм» происходит от algorithmi - латинской формы написания имени великого математика IX века аль-Хорезми, который сформулировал правила выполнения арифметических действий. Первоначально под алгоритмами и понимали только правила выполнения четырех арифметических действий над многозначными числами.