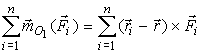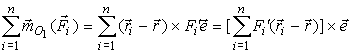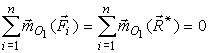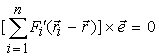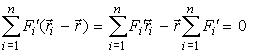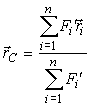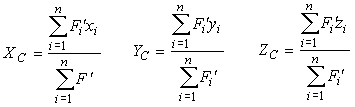2)Центр параллельных сил

Центром параллельных сил называется точка, через которую проходит эта равнодействующая при любых поворотах системы параллельных сил в пространстве. Д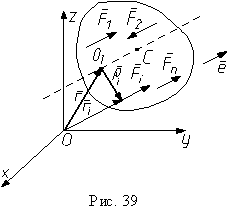 окажем, что центр параллельных сил существует и определим его координаты. Пусть система параллельных сил, эквивалентная равнодействующей, действует на твердое тело, а Q₁ - какая-либо точка на линии действия равнодействующей. Пусть так же r - радиус-вектор точки Q₁, а r_i - радиус-вектор точки приложения силы F_i (рис. 39). Вычислим сумму моментов всех сил системы относительно точки Q₁. Для этого построим радиус-вектор ρ_i, соединяющий точку Q₁ с точкой приложения силы F_i. Тогда

Но по рис. 39 r_i = r + ρ_i и ρ_i = r_i - r, следовательно,

(1)

Введем единичный вектор e, параллельный силам. Тогда любая сила системы может быть выражена как

(2)

где F_i' - проекция силы на направление единичного вектора, имеющая свой знак.

По рис. 39, например, F₁' положительна, а F₂' отрицательна. Подставляя в правую часть равенства (1) выражение (2), приписав в ней скалярный множитель к первому сомножителю векторного произведения, вынеся e за знак суммы, получаем

(3)

Для нахождения центра параллельных сил воспользуемся теоремой Вариньона. По теореме сумма моментов всех сил системы относительно точки O₁ должна быть равна нулю, так как точка O₁ лежит на линии действия равнодействующей R*:

(4)

Поэтому из (3) имеем

(5)

Так как e 0, то последнее равенство выполняется при любых поворотах системы сил и единичного вектора e только тогда, когда выражение в квадратных скобках равно нулю:

(6)

В свою очередь равенство (6) имеет единственное решение для радиус-вектора r, которое определяет положение центра параллельных сил, чем доказывается само существование центра параллельных сил. Обозначив центр параллельных сил точкой C (рис. 39), определим из уравнения (6) его радиус-вектор r_C:

(7)

Находим координаты центра параллельных сил, введя систему координат OXYZ с началом в O, проектируя на ее оси выражение (7):

(8)

В формулах (8) x_i, y_i, z_i являются координатами точек приложения сил системы, следовательно, числителями и знаменателями дробей будут алгебраические суммы.

Отметим, что выбор направления e, вдоль которого параллельные силы считаются положительными, произволен и не влияет на результаты вычисления координат центра параллельных сил (X_C, Y_C, Z_C) по формулам (8).

№28 Равновесие плоской системы параллельных сил.

Равновесие плоской системы параллельных сил.

В случае, когда все действующие на тело силы параллельны друг другу, мы можем направить ось Ох перпендикулярно к силам, а ось Оу параллельно им (рис. 29). Тогда проекция каждой из сил на Ox будет равна нулю и первое из 3-х равенств обратится в тождество вида 0 = 0. В результате для параллельных сил останется два условия равновесия:

Где ось Оу параллельна силам.

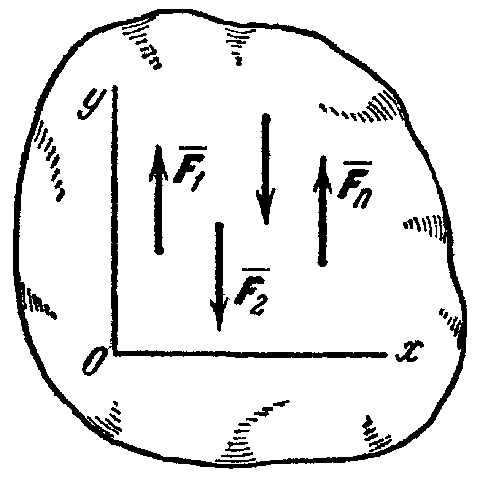
Рис.29

№30 Центр тяжести, и центр масс материальной системы.

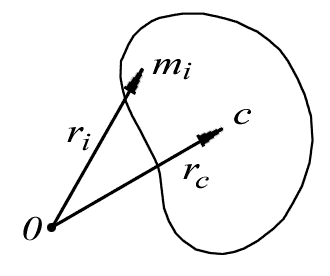
В любой системе частиц имеется одна замечательная точка С- центр инерции, или центр масс, - которая обладает рядом интересных и важных свойств. Центр масс является точкой приложения вектора импульса системы , так как вектор любого импульса является полярным вектором. Положение точки С относительно начала О данной системы отсчета характеризуется радиусом-вектором, определяемым следующей формулой:

(4.8)

где - масса и радиус-вектор каждой частицы системы, M - масса всей

системы (рис. 4.3).

Рис. 4.3. Определение центра масс системы частиц

Следует заметить, что центр масс системы совпадает с ее центром тяжести. Правда, это утверждение справедливо лишь в том случае, когда поле сил тяжести в пределах данной системы можно считать однородным.

Найдем скорость центра масс в данной системе отсчета. Продифференцировав (4.8) по времени, получим

(4.9)

Если скорость центра инерции равна нулю, то говорят, что система как целое покоится. Это вполне естественное обобщение понятия покоя отдельной частицы. Скорость же приобретает смысл скорости движения системы как целого.

Из формулы (4.9) с учетом (4.3) следует, что

(4.10)

т.е. импульс системы равен произведению массы системы на скорость ее центра масс.

Получим уравнение движения центра масс. Понятие центра масс позволяет придать уравнению (4.4) иную форму, которая часто оказывается более удобной. Для этого достаточно (4.10) подставить в (4.4), и учесть, что масса системы как таковой есть величина постоянная. Тогда получим

,

(4.11)

где - результирующая всех внешних сил, действующих на систему. Это и есть уравнение движения центра масс системы - одно из важнейших уравнений механики. В соответствии с этим уравнением, при движении любой системы частиц ее центр инерции движется так, как если бы вся масса системы была сосредоточена в этой точке и к ней были бы приложены все внешние силы, действующие на систему. При этом ускорение центра инерции совершенно не зависит от точек приложения внешних сил.

Далее, из уравнения (4.11) следует, что если то а значит, . В инерциальной системе отсчета такой случай реализуется для замкнутой системы. Кроме того, если , то, согласно (4.10); и импульс системы .

Таким образом, если центр масс системы движется равномерно и прямолинейно, то это означает, что ее импульс сохраняется в процессе движения. Разумеется, справедливо и обратное утверждение.

Уравнение (4.11). по форме совпадает с основным уравнением динамики материальной точки и является его естественным обобщением на систему частиц: ускорение системы как целого пропорционально результирующей всех внешних сил и обратно пропорционально суммарной массе системы. Напомним, что в неинерциальных системах отсчета результирующая всех внешних сил включает в себя как силы взаимодействия с окружающими телами, так и силы инерции.

Рассмотрим ряд примеров на движение центра масс системы.

Пример 1. Покажем, как можно решить задачу с человеком на плоту (стр. 90 )другим способом, воспользовавшись понятием центра масс.

Так как сопротивление воды пренебрежимо мало, то результирующая всех внешних сил, действующих на систему человек - плот, равна нулю. А это значит, что положение центра инерции данной системы в процессе движения человека (и плота) меняться не будет, т. е.

.

где и - радиус-векторы, характеризующие положения центров масс человека и плота относительно некоторой точки берега. Из этого равенства найдем связь между приращениями векторов и

Имея в виду, что приращения и представляют собой перемещения человека и плота относительно берега, найдем перемещение плота: