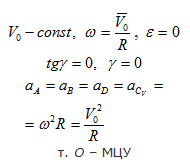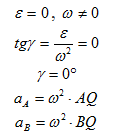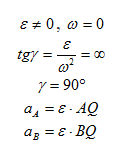- •Движение свободного твердого тела.
- •Задание движения свободного твердого тела.
- •Скорости и ускорения точек свободного твердого тела.
- •17. Основные аксиомы статики. Сложение сходящихся сил.
- •2)Центр параллельных сил
- •2)Определение координат тяжести однородного тела
- •Теоретическая механика кинематика
- •1.2. Первая задача динамики свободной точки
- •1.3. Вторая задача динамики свободной точки
- •2) Импульс силы
№1 .Способы задания движения точки. Уравнение движения и траектории точки.
Кинематика – раздел механики, в котором изучаются движение материальных тел с геометрической точки зрения, без учета массы и действующих на них сил. Способы задания движения точки: 1) естественный, 2) координатный, 3) векторный. Траектория точки – непрерывная кривая, которую описывает точка при своем движении.
Векторный способ.
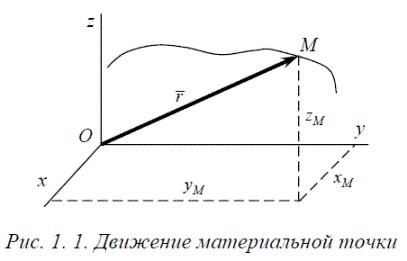
Положение точки определяется радиус-вектором (рис.1.1), проведённым в данную точку из неподвижного начала отсчёта.
r = r (t) ≡ OM (t).
С течением времени радиус-вектор будет изменяться, поэтому он является некоторой заданной векторной функцией времени r = r (t) . Это уравнение называется уравнением движения точки в векторной форме.
Непрерывная кривая, с точками которой в каждый момент времени совпадает движущаяся точка, называет траекторией. По отношению к различным системам отсчёта точка будет описывать разные кривые. Следовательно, траектория относительное понятие.
Геометрическое место концов переменного вектора называется годографом. Таким образом, траектория точки есть годограф радиусвектора этой точки.
Координатный способ.
Положение движущейся точки относительно выбранной системы отсчёта определяется её координатами в каждый момент времени (рис. 1.1): x = f1 t , y = f2 t , z = f3 t .
Функции f1 t , f2 t , f3 t . должны быть однозначными, непрерывными и, по крайней мере, дважды дифференцируемыми. Уравнения движения точки в координатной форме можно рассматривать и как уравнения траектории в параметрическом виде. Если исключить из этих уравнений параметрt , то получим уравнение траектории, как пересечение двух поверхностей
F1 (x, y) = 0, F2 (y, z) = 0.
Естественный способ.
Если известен вид траектории, то движение точки удобно задать естественным способом (рис. 1.2). Для этого на траектории назначают начало отсчёта (точка О), направление отсчёта и записывают зависимость дуговой координаты s от времени t.
![]()
Функция s = s (t) по самой природе механического движения должна быть непрерывной и однозначной.

С траекторией
точки можно связать естественный
координатный базис: единичные векторы
касательной -
 главной нормали -
главной нормали -
![]() и бинормали к траектории
и бинормали к траектории
![]() ,
Здесь ρ — радиус кривизны траектории.
,
Здесь ρ — радиус кривизны траектории.
Эти три вектора образуют естественный репер, вдоль них идут естественные оси. Координатные плоскости образуют сопровождающий трёхгранник и носят названия: плоскость (τ ,n ) — соприкасающаяся, плоскость ( n ,b ) — нормальная, плоскость (b ,τ ) — спрямляющая.
Уравнение движения и траектории точки
В этом случае главными параметрами, характеризующими движение точки но заданной траектории, являются: s – расстояние от заданного начального положения и t – время.
Величина, характеризующая в каждый данный момент времени направление и быстроту движения точки, называется скоростью (v на рис. 192). Вектор скорости всегда направлен вдоль касательной в ту сторону, куда движется точка. Числовое значение скорости в любой момент времени выражается производной от расстояния по времени:
v = ds/dt или v = f'(t).
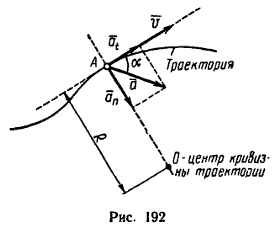
Ускорение a точки в каждый данный момент времени характеризует быстроту изменения скорости. При этом нужно отчетливо понимать, что скорость – вектор, и, следовательно, изменение скорости может происходить по двум признакам: по числовой величине (по модулю) и по направлению.
Быстрота изменения модуля скорости характеризуется касательным (тангенсальным) ускорением at – составляющей полного ускорения a, направленной по касательной к траектории (см. рис. 192).
Числовое значение касательного ускорения в общем случае определяется по формуле
at = dv/dt или at = f''(t). Быстрота изменения направления скорости характеризуется центростремительным (нормальным) ускорением an – составляющей полного ускорения a, направленного по нормали к траектории в сторону центра кривизны (см. рис. 192).
Числовое значение нормального ускорения определяется в общем случае по формуле
an = v2/R,
где v – модуль скорости точки в данный момент;
R – радиус кривизны траектории в месте, где находится точка в данный момент.
После того как определены касательное и нормальное ускорения, легко определить и ускорение a (полное ускорение точки).
Так как касательная и нормаль взаимно перпендикулярны, то числовое значение ускорения а можно определить при помощи теоремы Пифагора:
a = sqrt(at2 + an2).
Направление вектора a можно определить, исходя из тригонометрических соотношений, по одной из следующих формул:
sin α = an/a; cos α = at/a; tg α = an/at.
Но можно сначала определить направление полного ускорения a использовав формулу
tg α = an/at,
а затем найти числовое значение a:
a = an/sin α или a = at/cos α.
Касательное и нормальное ускорения точки являются главными кинематическими величинами, определяющими вид и особенности движения точки.
Наличие касательного ускорения (at≠0) или его отсутствие (at=0) определяют соответственно неравномерность или равномерность движения точки.
Наличие нормального ускорения (an≠0) или его отсутствие (an=0) определяют криволинейность или прямолинейность движения точки.
Движение точки можно классифицировать так:
а) равномерное прямолинейное (at = 0 и an = 0);
б) равномерное криволинейное (at = 0 и an ≠ 0);
в) неравномерное прямолинейное (at ≠ 0 и an = 0);
г) неравномерное криволинейное (at ≠ 0 и an ≠ 0).
Таким образом, движение точки классифицируется по двум признакам: по степени неравномерности движения и по виду траектории. Степень неравномерности движения точки задана уравнением s=f(t), а вид траектории задается непосредственно.
№2.Скорость и ускорение точки при задании движения в декартовых координатах.
№3.Скорость и ускорение точки при задании движения в полярных координатах.
№4.Скорость и ускорение точки при задании движении естественным способом.
Вектор скорости точки
Одной из основных кинематических характеристик движения точки является векторная величина, называемая скоростью точки.
Известно,
что при движении точки по прямой линии
с постоянной скоростью, равномерно,
скорость её определяется делением
пройденного расстояния s на время:
![]() При неравномерном движении эта формула
не годится. Введем сначала понятие о
средней скорости точки за какой-нибудь
промежуток времени. Пусть движущаяся
точка находится
При неравномерном движении эта формула
не годится. Введем сначала понятие о
средней скорости точки за какой-нибудь
промежуток времени. Пусть движущаяся
точка находится
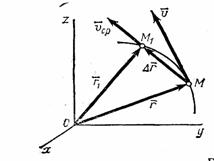
Рис. 5
в момент
времени t в положении М, определяемом
радиусом-вектором
![]() , а в момент
, а в момент
![]() приходит в положение M1 определяемое
вектором (рис.5). Тогда перемещение точки
за промежуток времени
приходит в положение M1 определяемое
вектором (рис.5). Тогда перемещение точки
за промежуток времени
![]() определяется вектором
определяется вектором
![]() который будем называть вектором
перемещения точки. Из треугольника ОММ1
видно, что
который будем называть вектором
перемещения точки. Из треугольника ОММ1
видно, что
![]() : следовательно ,
: следовательно ,
![]() .
.
Отношение
вектора перемещения точки к соответствующему
промежутку времени дает векторную
величину, называемую средней по модулю
и направлению скоростью точки за
промежуток времени
![]() .
.
![]()
Скоростью точки в данный момент времени t называется векторная величина v , к которой стремится средняя скорость vср при стремлении промежутка времени к нулю:
![]() ,
,
![]() .
.
Итак, вектор скорости точки в данный момент времени равен первой производной от радиуса-вектора точки по времени. Так как предельным направлением секущей ММ1 является касательная, то вектор скорости точки в данный момент времени направлен по касательной к траектории точки в сторону движения.
Определение скорости точки при координатном способе задания движения
Вектор
скорости точки
![]() учитывая, что
учитывая, что
![]() ,
,
![]() ,
,
![]() , найдем:
, найдем:
![]() ,
,
![]() ,
,
![]() .
.
Таким образом, проекции скорости точки на координатные оси равны первым производным от соответствующих координат точки по времени.
Зная
проекции скорости, найдем ее модуль и
направление (т.е. углы
![]() ,
,
![]() ,
,
![]() ,
которые вектор
,
которые вектор
![]() образует с координатными осями) по
формулам
образует с координатными осями) по
формулам
![]()
![]() ,
,
![]() ,
,
![]() ,
,
Итак, численная величина скорости точки в данный момент времени равна первой производной от расстояния (криволинейной координаты) s точки по времени.
Направлен вектор скорости по касательной к траектории, которая нам наперед известна.
Определение скорости точки при естественном способе задания движения
Величину
скорости можно определить как предел
(![]() - длина хорды
- длина хорды
![]() )
)
![]()
Где
![]() -
длина дуги
. Первый предел равен единице, второй
предел – производная
-
длина дуги
. Первый предел равен единице, второй
предел – производная
![]()
Следовательно,
скорость точки есть первая производная
по времени от закона движения:
![]() Направлен вектор скорости, как было
установлено ранее, по касательной к
траектории. Если величина скорости в
данный момент будет больше нуля, то
вектор скорости направляется в
положительном направлении.
Направлен вектор скорости, как было
установлено ранее, по касательной к
траектории. Если величина скорости в
данный момент будет больше нуля, то
вектор скорости направляется в
положительном направлении.
Вектор ускорения точки
Ускорением точки называется векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки. Пусть в некоторый момент времени t движущаяся точка находится в положении M и имеет скорость v , а в момент времени t1 приходит в положение M1 и имеет скорость v1 (рис 6.).
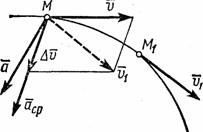
Рис.6
Тогда за
промежуток времени
скорость точки получает приращение
![]() .
.
Для
построения вектора
![]() отложим от точки М вектор
отложим от точки М вектор
![]() равный ? и построим параллелограмм, в
котором диагональю будет
, a одной из сторон
равный ? и построим параллелограмм, в
котором диагональю будет
, a одной из сторон
![]() Тогда, очевидно, вторая сторона и будет
изображать вектор
. Заметим, что вектор
всегда направлен в сторону вогнутости
траектории.
Тогда, очевидно, вторая сторона и будет
изображать вектор
. Заметим, что вектор
всегда направлен в сторону вогнутости
траектории.
Отношение приращения вектора скорости к соответствующему промежутку времени
определяет
вектор среднего ускорения точки за этот
промежуток времени:
![]() Вектор
среднего ускорения имеет то же направление,
что и вектор
т. е. направлен в сторону вогнутости
траектории.
Вектор
среднего ускорения имеет то же направление,
что и вектор
т. е. направлен в сторону вогнутости
траектории.
Ускорением
точки в данный момент времени t
называется векторная величина
![]() к которой стремится среднее ускорение
к которой стремится среднее ускорение
![]() при стремлении промежутка времени
к нулю: Вектор ускорения точки в данный
момент времени равен первой производной
от вектора скорости или второй производной
от радиуса-вектора точки по времени.
при стремлении промежутка времени
к нулю: Вектор ускорения точки в данный
момент времени равен первой производной
от вектора скорости или второй производной
от радиуса-вектора точки по времени.
Найдем, как располагается вектор по отношению к траектории точки.
При прямолинейном
движении вектор
![]() направлен вдоль прямой, по которой
движется точка.
направлен вдоль прямой, по которой
движется точка.
Если траекторией
точки является плоская кривая, то вектор
ускорения
,
так же как и вектор
![]() лежит
в плоскости этой кривой и направлен в
сторону ее вогнутости. Если траектория
не является плоской кривой, то вектор
направлен в сторону вогнутости траектории
и лежит в плоскости, проходящей через
касательную к траектории в точке М и
прямую, параллельную касательной в
соседней точке M1 (рис. 4). В пределе,
когда точка М стремится к М, эта плоскость
занимает положение так называемой
соприкасающейся плоскости, т.е. плоскости,
в которой происходит бесконечно малый
поворот касательной к траектории при
элементарном перемещении движущейся
точки. Следовательно, в общем случае
вектор ускорения
лежит в соприкасающейся плоскости и
направлен в сторону вогнутости кривой.
лежит
в плоскости этой кривой и направлен в
сторону ее вогнутости. Если траектория
не является плоской кривой, то вектор
направлен в сторону вогнутости траектории
и лежит в плоскости, проходящей через
касательную к траектории в точке М и
прямую, параллельную касательной в
соседней точке M1 (рис. 4). В пределе,
когда точка М стремится к М, эта плоскость
занимает положение так называемой
соприкасающейся плоскости, т.е. плоскости,
в которой происходит бесконечно малый
поворот касательной к траектории при
элементарном перемещении движущейся
точки. Следовательно, в общем случае
вектор ускорения
лежит в соприкасающейся плоскости и
направлен в сторону вогнутости кривой.
Рис. 4
Определение ускорения при координатном способе задания движения
Вектор ускорения
точки
![]() в проекции на оси получаем :
в проекции на оси получаем :
![]() ,
,
![]() ,
,
![]() ,
,
Или
![]() ,
,
![]() ,
,
![]() .
т.е. проекция ускорения точки на
координатные оси равны первым производным
от проекций скорости или вторым
производным от соответствующих координат
точки по времени. Модуль и направление
ускорения найдутся из формул.
.
т.е. проекция ускорения точки на
координатные оси равны первым производным
от проекций скорости или вторым
производным от соответствующих координат
точки по времени. Модуль и направление
ускорения найдутся из формул.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
Где,
![]() ,
,
![]() ,
,
![]() , - углы, образуемые вектором ускорения
с координатными осями.
, - углы, образуемые вектором ускорения
с координатными осями.
http://www.teoretmeh.ru/kinematika1.htm
Определение ускорения при естественном способе задания движения. Касательное и нормальное ускорение точки
При естественном
способе задания движения вектор
![]() определяют по его проекциям на оси
определяют по его проекциям на оси
![]() ,
имеющие начало в точке М
и движущиеся вместе с нею (рис.8). Эти
оси, называемые осями естественного
трехгранника (или скоростными
(естественными) осями), направлены
следующим образом: ось
,
имеющие начало в точке М
и движущиеся вместе с нею (рис.8). Эти
оси, называемые осями естественного
трехгранника (или скоростными
(естественными) осями), направлены
следующим образом: ось
![]() - вдоль касательной к траектории в
сторону положительного отсчета расстояния
s;
ось
- вдоль касательной к траектории в
сторону положительного отсчета расстояния
s;
ось
![]() - по нормали, лежащей в соприкасающейся
плоскости и направленной в сторону
вогнутости траектории; ось
- по нормали, лежащей в соприкасающейся
плоскости и направленной в сторону
вогнутости траектории; ось
![]() - перпендикулярно к первым двум так,
чтобы она образовала с ними правую
тройку. Нормаль
,
лежащая в соприкасающейся плоскости
(в
плоскости
самой кривой, если кривая плоская),
называется
главной
нормалью, а перпендикулярная к ней
нормаль
- бинормалью.
- перпендикулярно к первым двум так,
чтобы она образовала с ними правую
тройку. Нормаль
,
лежащая в соприкасающейся плоскости
(в
плоскости
самой кривой, если кривая плоская),
называется
главной
нормалью, а перпендикулярная к ней
нормаль
- бинормалью.

Рис.8
Было показано, что
ускорение точки
лежит в соприкасающейся плоскости, т.е.
в плоскости
![]() ;
следовательно, проекция вектора
на бинормаль равна нулю (
;
следовательно, проекция вектора
на бинормаль равна нулю (![]() ).
).
Вычислим проекции
,
на две другие оси. Пусть в момент
времени t
точка находится в положении М
и имеет скорость
![]() ,
a
в момент
,
a
в момент
![]() приходит в положение М1
и имеет скорость
приходит в положение М1
и имеет скорость
![]() .
.
Тогда по определению
![]() .
.
Перейдем в этом равенстве от векторов к их проекциям на оси и , проведенные в точке М (рис.8). Тогда на основании теоремы о проекции суммы (или разности) векторов на ось получим:
![]() ,
,
![]() .
.
Учитывая, что проекция
вектора на параллельные оси одинаковы,
проведем через точку М1
оси
![]() параллельные
параллельные
![]() и обозначим угол между направлением
вектора
и касательной
через
и обозначим угол между направлением
вектора
и касательной
через
![]() .
Этот угол между касательными к кривой
в точках М
и М1
называется углом смежности.
.
Этот угол между касательными к кривой
в точках М
и М1
называется углом смежности.
Напомним, что предел
отношения угла смежности
к длине дуги
![]() определяет кривизну k
кривой в точке
М.
Кривизна же является величиной, обратной
радиусу кривизны
определяет кривизну k
кривой в точке
М.
Кривизна же является величиной, обратной
радиусу кривизны
![]() в точке М.
Таким образом,
в точке М.
Таким образом,
![]() .
.
Обращаясь теперь к
чертежу (рис.9), находим, что проекции
векторов
![]() и
и
![]() на оси
будут
равны:
на оси
будут
равны:
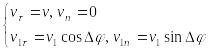 ,
,
где
и
- численные величины скорости точки в
моменты
![]() и
и
![]() .
.
Следовательно,
![]() .
.
Заметим что при
![]() точка М1
неограниченно приближается к М
и одновременно
точка М1
неограниченно приближается к М
и одновременно
![]() .
.
Тогда, учитывая, что
в пределе
![]() ,
получим для
,
получим для
![]() выражение
выражение
![]() .
.
Правую часть выражения
![]() преобразуем так, чтобы в нее вошли
отношения, пределы которых нам известны.
Для этого умножим числитель и знаменатель
дроби, стоящей под знаком предела, на
преобразуем так, чтобы в нее вошли
отношения, пределы которых нам известны.
Для этого умножим числитель и знаменатель
дроби, стоящей под знаком предела, на
![]() .
Тогда будем иметь
.
Тогда будем иметь
![]() ,
,
так как пределы каждого из стоящих в скобке сомножителей при равны:
![]()
Окончательно получаем:
![]() .
.
Итак, мы доказали,
что проекция ускорения точки на
касательную равна первой производной
от численной величины скорости или
второй производной от расстояния
(криволинейной координаты)
s
no
времени, а проекция ускорения на главную
нормаль равна квадрату скорости деленному
на радиус кривизны траектории в данной
точке кривой; проекция ускорения на
бинормаль равна нулю (![]() ).
Эти результаты выражают собою одну из
важных теорем кинематики точки.
).
Эти результаты выражают собою одну из
важных теорем кинематики точки.
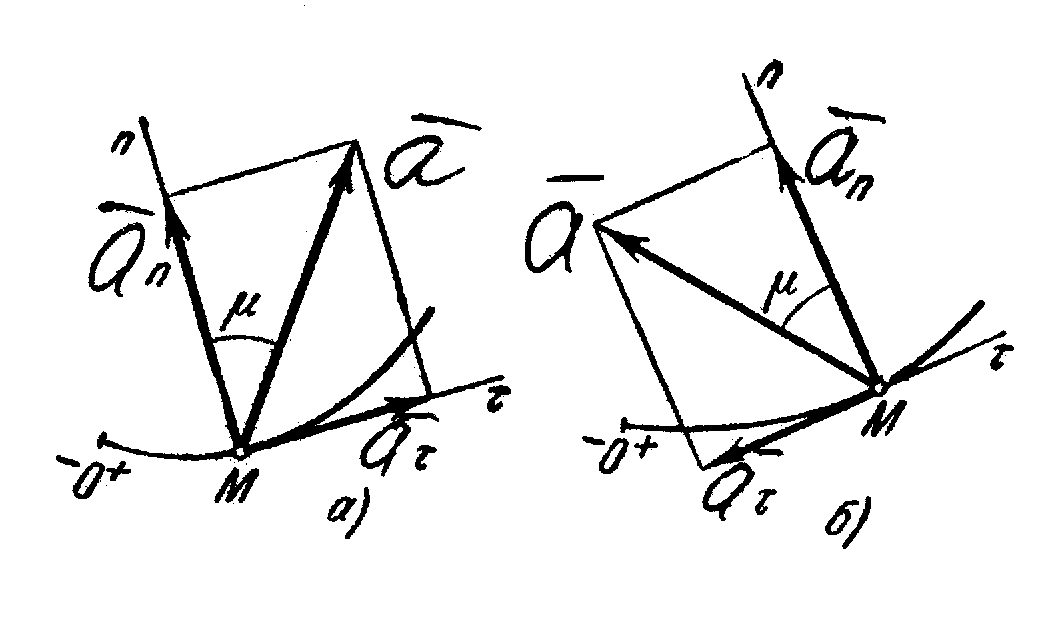
Рис.9
Отложим вдоль
касательной
и главной нормали
векторы
![]() и
и
![]() ,
численно равные
и
(рис. 9). Эти векторы изображают касательную
и нормальную составляющие ускорения
точки. При этом составляющая
будет всегда направлена в сторону
вогнутости кривой (величина a
всегда положительна), а составляющая
может быть направлена или в положительном,
или в отрицательном направлении оси
в зависимости от знака проекции
(см. рис.9, а и б).
,
численно равные
и
(рис. 9). Эти векторы изображают касательную
и нормальную составляющие ускорения
точки. При этом составляющая
будет всегда направлена в сторону
вогнутости кривой (величина a
всегда положительна), а составляющая
может быть направлена или в положительном,
или в отрицательном направлении оси
в зависимости от знака проекции
(см. рис.9, а и б).
Вектор ускорения точки изображается диагональю параллелограмма, построенного на составляющих и . Так как эти составляющие взаимно перпендикулярны, то по модулю:
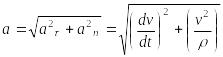 .
.
Некоторые частные случаи движения точки
Пользуясь полученными результатами, рассмотрим некоторые частные случаи движения точки.
1) Прямолинейное
движение. Если траекторией точки является
прямая линия, то
![]() .
Тогда
.
Тогда
![]() и все ускорение точки равно одному
только касательному ускорению:
и все ускорение точки равно одному
только касательному ускорению:
![]() .
.
Так как в данном случае скорость изменяется только численно, то отсюда заключаем, что касательное ускорение характеризует изменение скорости по численной величине.
2) Равномерное
криволинейное движение. Равномерным
называется такое криволинейное движение
точки, в котором численная величина
скорости все время остается постоянной:
![]() .
.
Тогда
![]() и все ускорение точки равно одному
только нормальному:
и все ускорение точки равно одному
только нормальному:
![]() .
.
Вектор ускорения
![]() направлен при этом все время по нормали
к траектории точки.
направлен при этом все время по нормали
к траектории точки.
Так как в данном случае ускорение появляется только за счет изменения направления скорости, то отсюда заключаем, что нормальное ускорение характеризует изменение скорости по направлению. Найдем закон равномерного криволинейного движения.
Из формулы
![]() имеем
имеем
![]() .
.
Пусть в начальный
момент (![]() )
точка находится от начала отсчета на
расстоянии
)
точка находится от начала отсчета на
расстоянии
![]() .
Тогда, беря от левой и правой части
равенства определенные интегралы в
соответствующих пределах, получим
.
Тогда, беря от левой и правой части
равенства определенные интегралы в
соответствующих пределах, получим
![]() или
или
![]() ,
,
так как . Окончательно находим закон равномерного криволинейного движения в виде
![]() .
.
Если
![]() ,
то s
даст путь, пройденный точкой за время
t.
Следовательно, при равномерном движении
путь, пройденный точкой, расчет
пропорционального времени, а скорость
движения равна отношению пути ко времени
,
то s
даст путь, пройденный точкой за время
t.
Следовательно, при равномерном движении
путь, пройденный точкой, расчет
пропорционального времени, а скорость
движения равна отношению пути ко времени
![]() .
.
3) Равномерное
прямолинейное движение. В этом случае
![]() ,
а значит и
.
Заметим, что единственным движением, в
котором ускорение точки все время равно
нулю, является равномерное прямолинейное
движение.
,
а значит и
.
Заметим, что единственным движением, в
котором ускорение точки все время равно
нулю, является равномерное прямолинейное
движение.
4) Равнопеременное
криволинейное движение. Равнопеременным
называется такое криволинейное движение
точки, при котором касательное ускорение
остается все время величиною постоянной:
![]() .
Найдем закон этого движения, считая,
что при
:
.
Найдем закон этого движения, считая,
что при
:
![]() ,
а
,
а
![]() ,
где
,
где
![]() - начальная скорость точки. Согласно
формуле
- начальная скорость точки. Согласно
формуле
![]() имеем
имеем
![]() .
.
Так как , то, беря от обеих частей последнего равенства интегралы в соответствующих пределах, получим:
![]() .
.
Формулу представим в виде
![]() или
или
![]() .
.
Вторично интегрируя, найдем закон равнопеременного криволинейного движения точки в виде
![]() .
.
Если при криволинейном движении точки модуль скорости возрастает, то движение называется ускоренным, а если убывает - замедленным.
№5.Основная теорема поля скоростей твердого тела. (?)
№6. Посторение поля скоростей твердого тела по скоростям трех его точек.(?)
№7.Поступательное движение твердого тела. Скорости и ускорения точек тела.
Абсолютно твердым телом называется материальное тело, геометрическая форма которого и размеры не изменяются ни при каких механических воздействиях со стороны других тел, а расстояние между любыми двумя его точками остается постоянным.
В твердом теле скорости точек распределяются таким образом, что проекции скоростей двух точек на прямую, их соединяющую, равны между собой (кинематическое определение твердого тела).
Положение твердого тела в общем случае определяется шестью параметрами; в частных случаях, когда на движение тела наложены ограничения, число параметров соответственно уменьшается.
Поступательным движением твердого тела называется такое его движение, при котором всякая прямая, неизменно связанная с телом, перемещается параллельно самой себе. Для этого достаточно, чтобы две непараллельные прямые, связанные с телом, перемещались параллельно самим себе. При поступательном движении все точки тела описывают одинаковые, параллельно расположенные траектории и имеют в любой момент времени одинаковые скорости и ускорения. Таким образом, поступательное движение тела определяется движением одной его точки О.
Теорема. При поступательном движении твердого тела траектории, скорости и ускорения точек тела одинаковы.
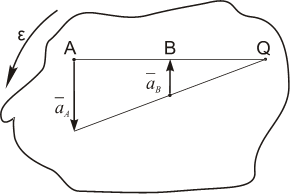
Доказательство. Если выбрать две точки твердого тела А и В (рисунок 1.2), то радиусы-векторы этих точек связаны соотношением
![]()
Траектория точки А – это кривая, которая задается функцией rA(t), а траектория точки B – это кривая, которая задается функцией rB(t). Траектория точки B получается переносом траектории точки A в пространстве вдоль вектора AB, который не меняет своей величины и направления во времени (AB = const). Следовательно, траектории всех точек твердого тела одинаковы.
Продифференцируем по времени выражение
![]()
Получаем
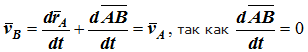
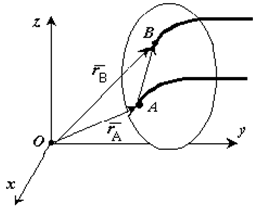
Рис. 1.2
Продифференцируем по времени скорость и получим выражение aB = aA. Следовательно, скорости и ускорения всех точек твердого тела одинаковы.
Для задания поступательного движения твердого тела достаточно задать движение одной из его точек:

№8.Вращение твердого тела вокруг неподвижной оси. Скорости и ускорения точек тела.
Вращением твердого тела вокруг неподвижной оси называют движение, при котором хотя бы две точки тела все время остаются неподвижными. Прямая, проходящая через эти точки, называется осью вращения.

Рисунок 2.3
Вращательное движение определяется двугранным углом φ между двумя плоскостями, проходящими через ось вращения. Одна из этих плоскостей неподвижна, вторая скреплена с твердым телом и поворачивается вместе с ним (рисунок 2.3).
Изменение этого угла с течением времени и есть закон вращательного движения:
φ=φ(t), рад. (2.2)
Положительным считается угол, откладываемый против хода часовой стрелки, если смотреть навстречу выбранному направлению оси вращения (ось Oz на рисунке 2.3). Угол измеряется в радианах.
Быстрота изменения угла φ – это угловая скорость:
ω=dφ/dt=φ', рад/с; с-1. (2.3)
Приняв k как единичный орт положительного направления оси, получим
![]()
Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.
Изменение угловой скорости характеризуется угловым ускорением:
![]()
Вектор углового ускорения, как и вектор угловой скорости, направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном - противоположны.
Для некоторых частных случаев вращательного движения могут быть использованы формулы:
- равномерное вращение ( ω - const)
φ=φ0+ωt; (2.5)
- равнопеременное вращение ( ε - const)
ω=ω0+εt; φ=φ0+ω0t+εt2/2. (2.6)
В технике угловая скорость часто задается в оборотах в минуту n[об/мин]. Один оборот – это 2π радиан:
ω=n⋅2π/60=nπ/30 рад/с; с-1.
http://www.isopromat.ru/teormeh/obzornyj-kurs/vrashenie-tverdogo-tela-vokrug-nepodvizhnoj-osi
№9.Плоскопараллельное движение твердого тела.Исследование плоского поля скоростей.
Плоскопараллельным (или плоским) называется такое движение твердого тела, при, котором все его точки перемещаются параллельно некоторой фиксированной плоскости П (рис. 28). Плоское движение совершают многие части механизмов и машин, например катящееся колесо на прямолинейном участке пути, шатун в кривошипно-ползунном механизме и др. Частным случаем плоскопараллельного движения является вращательное движение твердого тела вокруг неподвижной оси.
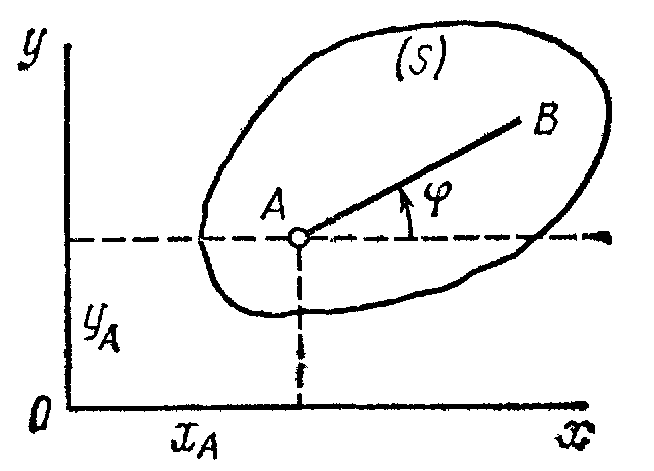
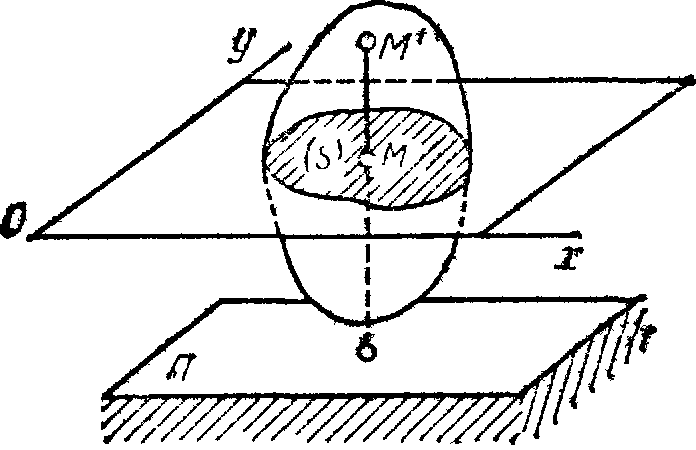
Рис.28 Рис.29
Рассмотрим сечение S тела какой-нибудь плоскости Оxy, параллельной плоскости П (рис.29). При плоскопараллельном движении все точки тела, лежащие на прямой ММ’, перпендикулярной течению S, т. е. плоскости П, движутся тождественно.
Отсюда заключаем, что для изучения движения всего тела достаточно изучить, как движется в плоскости Оху сечение S этого тела или некоторая плоская фигура S. Поэтому в дальнейшем вместо плоского движения тела будем рассматривать движение плоской фигуры S в ее плоскости, т.е. в плоскости Оху.
Положение фигуры S
в плоскости Оху
определяется
положением какого-нибудь проведенного
на этой фигуре отрезка АВ
(рис. 28). В свою очередь положение отрезка
АВ
можно определить, зная координаты
![]() и
и
![]() точки А
и угол
точки А
и угол
![]() ,
который отрезок АВ
образует с осью
х. Точку А,
выбранную для определения положения
фигуры S,
будем в дальнейшем называть полюсом.
,
который отрезок АВ
образует с осью
х. Точку А,
выбранную для определения положения
фигуры S,
будем в дальнейшем называть полюсом.
При движении фигуры величины и и будут изменяться. Чтобы знать закон движения, т. е. положение фигуры в плоскости Оху в любой момент времени, надо знать зависимости
![]() .
.
Уравнения, определяющие закон происходящего движения, называются уравнениями движения плоской фигуры в ее плоскости. Они же являются уравнениями плоскопараллельного движения твердого тела.
Первые два из
уравнений движения определяют то
движение, которое фигура совершала бы
при
=const;
это, очевидно, будет поступательное
движение, при котором все точки фигуры
движутся так же, как полюс А.
Третье уравнение определяет движение,
которое фигура совершала бы при
![]() и
и
![]() , т.е. когда полюс А
неподвижен;
это будет вращение фигуры вокруг
полюса А.
Отсюда можно заключить, что в общем
случае движение плоской фигуры в ее
плоскости может рассматриваться как
слагающееся из поступательного
движения, при котором все точки фигуры
движутся так же, как полюс А,
и из вращательного движения вокруг
этого полюса.
, т.е. когда полюс А
неподвижен;
это будет вращение фигуры вокруг
полюса А.
Отсюда можно заключить, что в общем
случае движение плоской фигуры в ее
плоскости может рассматриваться как
слагающееся из поступательного
движения, при котором все точки фигуры
движутся так же, как полюс А,
и из вращательного движения вокруг
этого полюса.
Основными
кинематическими характеристиками
рассматриваемого движения являются
скорость и ускорение поступательного
движения, равные скорости и ускорению
полюса
![]() ,
,
![]() ,
а также угловая скорость
,
а также угловая скорость
![]() и угловое ускорение
и угловое ускорение
![]() вращательного движения вокруг полюса.
вращательного движения вокруг полюса.
Определение скоростей точек плоской фигуры
Было отмечено, что
движение плоской фигуры можно рассматривать
как слагающееся из поступательного
движения, при котором все точки фигуры
движутся со скоростью
![]() полюса А,
и из вращательного движения вокруг
этого полюса. Покажем, что скорость
любой точки М
фигуры
складывается геометрически из скоростей,
которые точка получает в каждом из этих
движений.
полюса А,
и из вращательного движения вокруг
этого полюса. Покажем, что скорость
любой точки М
фигуры
складывается геометрически из скоростей,
которые точка получает в каждом из этих
движений.
В самом деле, положение
любой точки М
фигуры определяется по отношению к осям
Оху
радиусом-вектором
![]() (рис.30), где
(рис.30), где
![]() -
радиус-вектор полюса А,
-
радиус-вектор полюса А,
![]() -
вектор, определяющий положение точки
М
относительно осей
-
вектор, определяющий положение точки
М
относительно осей
![]() ,
перемещающихся вместе с полюсом А
поступательно
(движение фигуры по отношению к этим
осям представляет собой вращение вокруг
полюса А).
Тогда
,
перемещающихся вместе с полюсом А
поступательно
(движение фигуры по отношению к этим
осям представляет собой вращение вокруг
полюса А).
Тогда
![]() .
.
В полученном равенстве
величина
![]() есть скорость полюса А;
величина же
есть скорость полюса А;
величина же
![]() равна скорости
равна скорости
![]() ,
которую точка М
получает при
,
которую точка М
получает при
![]() ,
т.е. относительно осей
,
т.е. относительно осей
![]() ,
или, иначе говоря, при вращении фигуры
вокруг полюса А.
Таким образом, из предыдущего равенства
действительно следует, что
,
или, иначе говоря, при вращении фигуры
вокруг полюса А.
Таким образом, из предыдущего равенства
действительно следует, что
![]() .
.
Скорость , которую точка М получает при вращении фигуры вокруг полюса А:
![]()
![]() ,
,
где - угловая скорость фигуры.
Таким образом,
скорость любой точки М
плоской фигуры геометрически складывается
из скорости какой-нибудь другой точки
А,
принятой за полюс, и скорости, которую
точка М
получает при вращении фигуры вокруг
этого полюса. Модуль и направление
скорости
![]() находятся построением соответствующего
параллелограмма (рис.31).
находятся построением соответствующего
параллелограмма (рис.31).
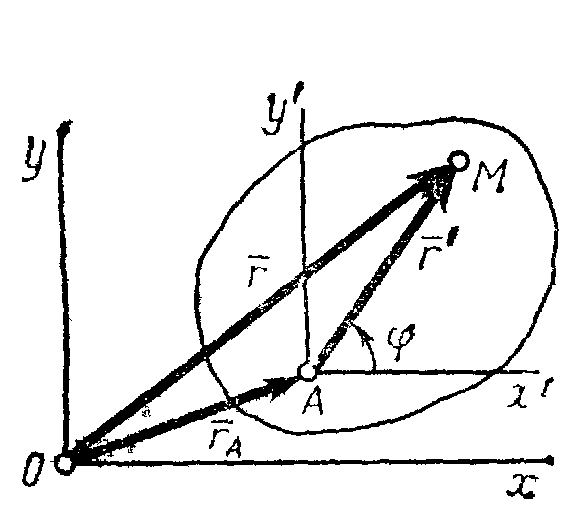
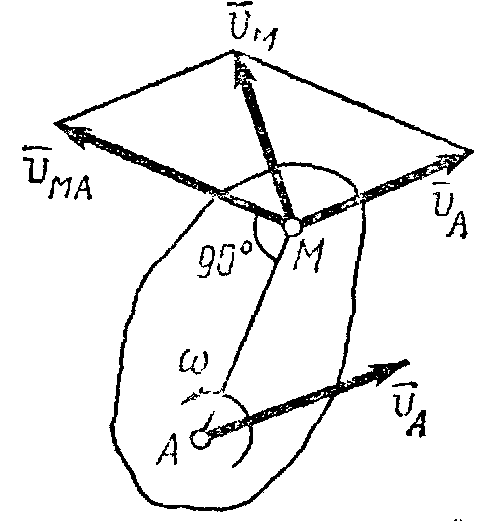
Рис.30 Рис.31
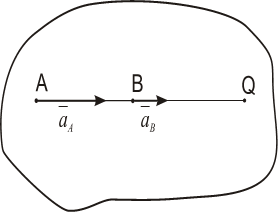
Теорема о проекциях скоростей двух точек тела
Определение скоростей точек плоской фигуры (или тела, движущегося плоскопараллельно) связано обычно с довольно сложными расчетами. Однако можно получить ряд других, практически более удобных и простых методов определения скоростей точек фигуры (или тела).
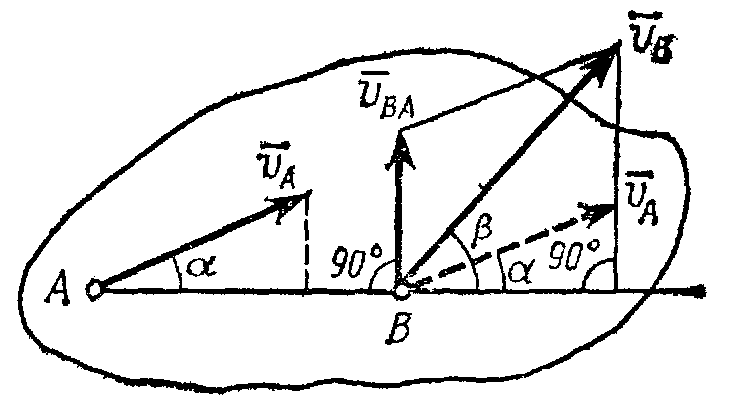
Рис.32
Один из таких методов
дает теорема: проекции скоростей
двух точек твердого тела на ось, проходящую
через эти точки, равны друг другу.
Рассмотрим какие-нибудь две точки А
и В
плоской фигуры (или тела). Принимая точку
А
за полюс (рис.32), получаем
![]() .
Отсюда, проектируя обе части равенства
на ось, направленную по АВ,
и учитывая, что вектор
.
Отсюда, проектируя обе части равенства
на ось, направленную по АВ,
и учитывая, что вектор
![]() перпендикулярен АВ,
находим
перпендикулярен АВ,
находим
![]()
и теорема доказана.
Определение скоростей точек плоской фигуры с помощью мгновенного центра скоростей.
Другой простой и наглядный метод определения скоростей точек плоской фигуры (или тела при плоском движении) основан на понятии о мгновенном центре скоростей.
Мгновенным центром скоростей называется точка плоской фигуры, скорость которой в данный момент времени равна нулю.
Легко убедиться,
что если фигура движется непоступательно,
то такая точка в каждый момент времени
t
существует и притом единственная. Пусть
в момент времени t
точки А
и В
плоской фигуры имеют скорости
![]() и
и
![]() ,
не параллельные друг другу (рис.33). Тогда
точка Р,
лежащая на пересечении перпендикуляров
Аа
к вектору
и Вb
к вектору
,
и будет мгновенным центром скоростей
так как
,
не параллельные друг другу (рис.33). Тогда
точка Р,
лежащая на пересечении перпендикуляров
Аа
к вектору
и Вb
к вектору
,
и будет мгновенным центром скоростей
так как
![]() .
В самом деле, если допустить, что
,
то по теореме о проекциях скоростей
вектор
.
В самом деле, если допустить, что
,
то по теореме о проекциях скоростей
вектор
![]() должен быть одновременно перпендикулярен
и АР
(так как
должен быть одновременно перпендикулярен
и АР
(так как
![]() )
и ВР
(так как
)
и ВР
(так как
![]() ),
что невозможно. Из той же теоремы видно,
что никакая другая точка фигуры в
этот момент времени не может иметь
скорость, равную нулю.
),
что невозможно. Из той же теоремы видно,
что никакая другая точка фигуры в
этот момент времени не может иметь
скорость, равную нулю.

Рис.33
Если теперь в момент времени взять точку Р за полюс, то скорость точки А будет
![]() ,
,
так как . Аналогичный результат получается для любой другой точки фигуры. Следовательно, скорости точек плоской фигуры определяются в данный момент времени так, как если бы движение фигуры было вращением вокруг мгновенного центра скоростей. При этом
![]()
![]() и т.д.
и т.д.
Из равенств, следует еще, что
![]()
т.е. что скорости точек плоской фигуры пропорциональны их расстояниям от МЦС.
Полученные результаты приводят к следующим выводам.
1. Для определения мгновенного центра скоростей надо знать только направления скоростей и каких-нибудь двух точек А и В плоской фигуры (или траектории этих точек); мгновенный центр скоростей находится в точке пересечения перпендикуляров, восставленных из точек А и В к скоростям этих точек (или к касательным к траекториям).
2. Для определения
скорости любой точки плоской фигуры,
надо знать модуль и направление скорости
какой-нибудь одной точки А
фигуры и направление скорости другой
ее точки В.
Тогда, восставив из точек А
и В
перпендикуляры к
и
,
построим мгновенный центр скоростей
Р
и по направлению
определим
направление поворота фигуры. После
этого, зная
,
найдем скорость
любой точки
М
плоской фигуры. Направлен вектор
![]() перпендикулярно
РМ в сторону
поворота фигуры.
перпендикулярно
РМ в сторону
поворота фигуры.
3. Угловая скорость плоской фигуры равна в каждый данный момент времени отношению скорости какой-нибудь точки фигуры к ее расстоянию от мгновенного центра скоростей Р:
![]() .
.
Рассмотрим некоторые частные случаи определения мгновенного центра скоростей.
а) Если плоскопараллельное движение осуществляется путем качения без скольжения одного цилиндрического тела по поверхности другого неподвижного, то точка Р катящегося тела, касающаяся неподвижной поверхности (рис.34), имеет в данный момент времени вследствие отсутствия скольжения скорость, равную нулю ( ), и, следовательно, является мгновенным центром скоростей. Примером служит качение колеса по рельсу.
б) Если скорости
точек А
и В
плоской фигуры параллельны друг другу,
причем линия АВ
не перпендикулярна
(рис.35,а), то мгновенный центр скоростей
лежит в бесконечности и скорости всех
точек параллельны
.
При этом из теоремы о проекциях скоростей
следует, что
![]() т. е.
т. е.
![]() ;
аналогичный результат получается для
всех других точек. Следовательно, в
рассматриваемом случае скорости
всех точек фигуры в данный момент времени
равны друг другу и по модулю, и по
направлению, т.е. фигура имеет мгновенное
поступательное распределение скоростей
(такое состояние движения тела называют
еще мгновенно поступательным). Угловая
скорость
тела в этот момент времени, как видно
равна нулю.
;
аналогичный результат получается для
всех других точек. Следовательно, в
рассматриваемом случае скорости
всех точек фигуры в данный момент времени
равны друг другу и по модулю, и по
направлению, т.е. фигура имеет мгновенное
поступательное распределение скоростей
(такое состояние движения тела называют
еще мгновенно поступательным). Угловая
скорость
тела в этот момент времени, как видно
равна нулю.
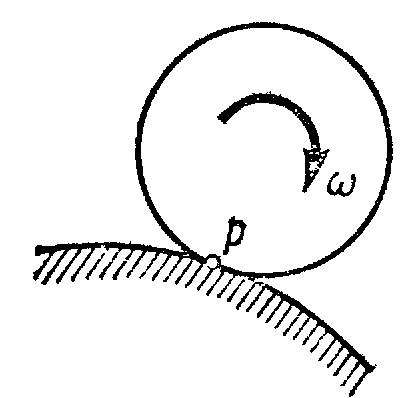
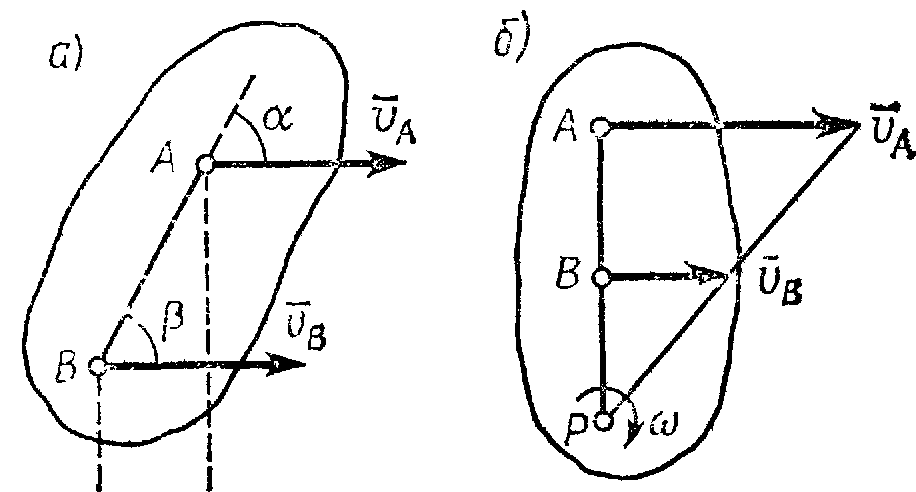
Рис.34 Рис.35
в) Если скорости
точек А
и В
плоской фигуры параллельны друг другу
и при этом линия АВ
перпендикулярна
,
то мгновенный
центр скоростей Р
определяется построением, показанным
на рис. 35,б. Справедливость построений
следует из пропорции. В этом случае, в
отличие от предыдущих, для нахождения
центра Р
надо кроме направлений знать еще и
модули скоростей
![]() и
.
и
.
г) Если известны
вектор скорости
какой-нибудь точки В
фигуры и ее угловая скорость
,
то положение мгновенного центра скоростей
Р,
лежащего на перпендикуляре к
(рис.35,б),
можно найти как
![]() .
.
№10. Общая формула плоского поля ускорений. Мгновенный центр ускорений.
Мгнове́нный центр ускоре́ний — при непоступательном движении точка, находящаяся в плоскости движения тела, ускорение которой в данный момент времени равно нулю.
Положение мгновенного центра ускорений в общем случае не совпадает с положением мгновенного центра скоростей. Однако в некоторых случаях, например, при чисто вращательном движении, положение этих двух точек может совпадать.
Для
того, чтобы определить положение
мгновенного центра ускорений, необходимо
к векторам ускорений двух различных
точек тела провести прямые под равными
углами
![]() .
В точке пересечения проведённых прямых
и будет находиться мгновенный центр
ускорений. Угол
должен
удовлетворять равенству:
.
В точке пересечения проведённых прямых
и будет находиться мгновенный центр
ускорений. Угол
должен
удовлетворять равенству:
![]()
Где
![]() —
угловое
ускорение
тела;
—
угловое
ускорение
тела;
![]() —
угловая
скорость тела.
—
угловая
скорость тела.
Мгнове́нный центр скоросте́й — при плоскопараллельном движении точка, обладающая следующими свойствами: а) её скорость в данный момент времени равна нулю; б) относительно неё в данный момент времени вращается тело.
Враща́тельное движе́ние — вид механического движения. При вращательном движении абсолютно твёрдого тела его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения в данной системе отсчёта может быть как подвижной, так и неподвижной. Например, в системе отсчёта, связанной с Землёй, ось вращения ротора генератора на электростанции неподвижна.При выборе некоторых осей вращения, можно получить сложное вращательное движение - сферическое движение, когда точки тела движутся по сферам.
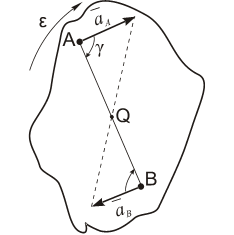
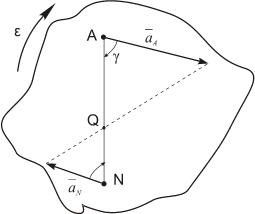
В учебной литературе доказывается, что при движении фигуры в плоскости в каждый момент времени существует такая точка плоской фигуры, ускорение которой в этот момент равно нолю. Эту точку называют мгновенным центром ускорений (МЦУ). В наших рассуждениях будем обозначать ее буквой Q. Взяв эту точку за полюс, получим формулу для определения ускорения произвольной точки:

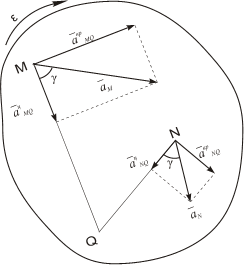
Рис. 1.12
Угол, который составляет вектор ускорения точки М с линией MQ определится из соотношения:
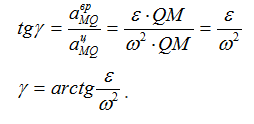
Т.е. у всех точек плоской фигуры этот угол одинаков. Из рис. 1.12 видно, что мгновенный центр ускорений лежит в точке пересечения линий, составляющих угол γ с соответствующими ускорениями точек.
На рис. 1.13-1.15 приведены частные случаи определения положения мгновенного центра ускорений.
|
Рис. 1.13б
|
Рис. 1.14а
|
Рис. 1.14б
|
Рис. 1.15а
|
Рис. 1.15б
|
№11.Вращение твердого тела вокруг неподвижного центра. Кинематическое уравнение Эйлера. Скорости и ускорения точек тела.
Кинематические Э. у. дают выражения wх, wу, wz через Эйлеровы углы j, y, q и имеют вид:
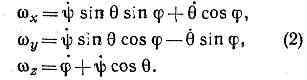
Эта система уравнений позволяет, зная закон движения тела, определить момент действующих на него сил и, наоборот, зная действующие на тело силы, определить закон его движения.
Скорости и ускорения точек вращающегося тела.
Установив характеристики движения всего тела в целом, перейдем к изучению движения отдельных его точек.
1. Скорости точек
тела. Рассмотрим какую-нибудь точку М
твердого тела, находящуюся на расстоянии
h
от оси вращения (см. рис.13). При вращении
тела точка М
будет описывать окружность радиуса h,
плоскость которой перпендикулярна оси
вращения, а центр С
лежит на самой оси. Если за время
![]() происходит элементарный поворот
тела на угол
происходит элементарный поворот
тела на угол
![]() ,
то точка М
при этом совершает вдоль своей траектории
элементарное перемещение
,
то точка М
при этом совершает вдоль своей траектории
элементарное перемещение
![]() .
Тогда числовое значение скорости точки
будет равно отношению
.
Тогда числовое значение скорости точки
будет равно отношению
![]() к
,
т.е
к
,
т.е
![]() или
или
![]() .
.
Скорость в отличие от угловой скорости тела называют иногда еще линейной или окружной скоростью точки М.
Таким образом, числовое значение скорости точки вращающегося твердого тела равно произведению угловой скорости тела на расстояние от этой точки до оси вращения.
Направлена скорость по касательной к описываемой точкой окружности или перпендикулярно плоскости, проходящей через ось вращения и точку М.
Так как для всех точек тела имеет в данный момент времени одно и то же значение, то скорости точек вращающегося тела пропорциональны их расстояниям от оси вращения.
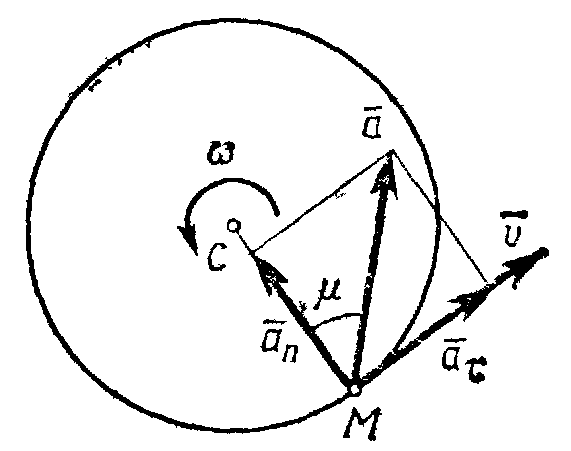
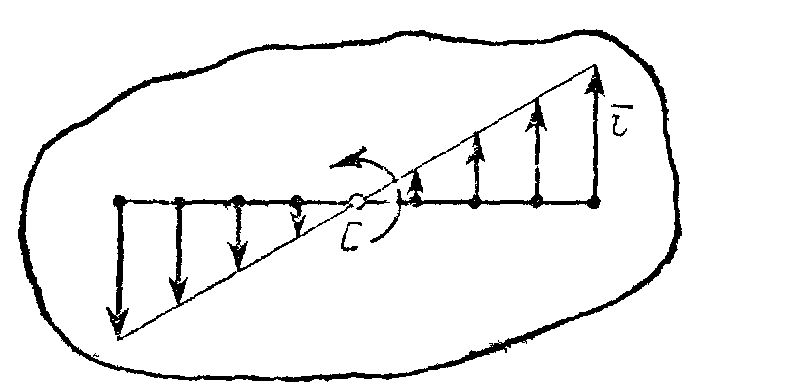
Рис.15 Рис. 16
2. Ускорения точек
тела. Для нахождения ускорения точки М
воспользуемся формулами
![]() ,
,
![]() .
.
В нашем случае
![]() .
Подставляя значение
в выражения
и
,
получим:
.
Подставляя значение
в выражения
и
,
получим:
![]()
![]()
или окончательно:
![]() ,
,
![]() .
.
Касательная
составляющая ускорения
направлена по касательной к траектории
(в сторону движения при ускоренном
вращении тела и в обратную сторону
при, замедленном); нормальная составляющая
![]() всегда направлена по радиусу МС
к оси вращения (рис.16). Полное ускорение
точки М будет
всегда направлена по радиусу МС
к оси вращения (рис.16). Полное ускорение
точки М будет
![]() или
или
![]() .
.
Отклонение вектора
полного ускорения от радиуса описываемой
точкой окружности определяется углом
![]() ,
который вычисляется по формуле
,
который вычисляется по формуле
![]() .
Подставляя сюда значения
и
,
получаем
.
Подставляя сюда значения
и
,
получаем
![]() .
.
Так как и имеют в данный момент времени для всех точек тела одно и то же значение, то ускорения всех точек вращающегося твердого тела пропорциональны их расстояниям от оси вращения и образуют в данный момент времени один и тот же угол с радиусами описываемых ими окружностей. Поле ускорений точек вращающегося твердого тела имеет вид, показанный на рис.18.
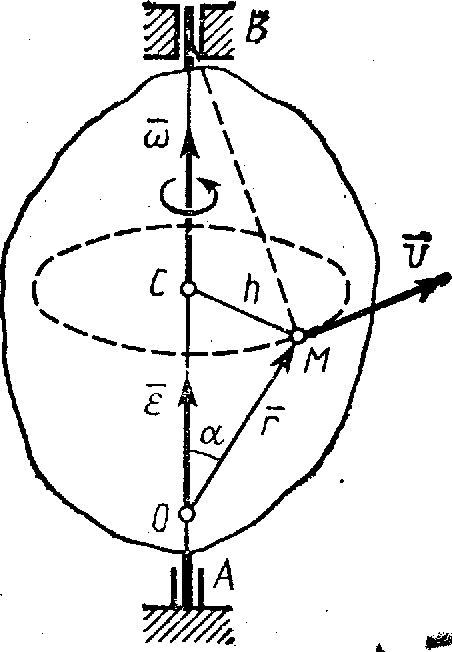
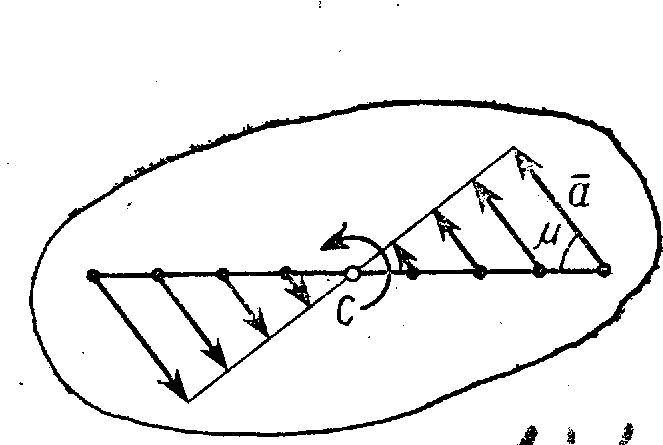
Рис.17 Рис.18
3. Векторы скорости
и ускорения точек тела. Чтобы найти
выражения непосредственно для векторов
и
![]() ,
проведем из произвольной точки О
оси АВ
радиус-вектор
,
проведем из произвольной точки О
оси АВ
радиус-вектор
![]() точки М
(рис. 17). Тогда
точки М
(рис. 17). Тогда
![]() и по формуле
и по формуле
![]() или
или
![]() .
.
Таким образом, модуль
векторного произведения
![]() равен модулю скорости точки М.
Направления векторов
и
тоже совпадают (оба они перпендикулярны
плоскости ОМВ)
и размерности их одинаковы.
Следовательно,
равен модулю скорости точки М.
Направления векторов
и
тоже совпадают (оба они перпендикулярны
плоскости ОМВ)
и размерности их одинаковы.
Следовательно,
![]() - формула Эйлера, т.е. вектор скорости
любой точки вращающегося тела равен
векторному произведению угловой скорости
тела на радиус-вектор этой точки.
- формула Эйлера, т.е. вектор скорости
любой точки вращающегося тела равен
векторному произведению угловой скорости
тела на радиус-вектор этой точки.
№12.Движение свободного твердого тела.Исследование общего поля скоростей. Мгновенно-винтовое движение.
Движение свободного твердого тела.
Напомним, что свободное твердое тело имеет шесть степеней свободы, а его движение является общим случаем движения твердого тела.
Задание движения свободного твердого тела.
О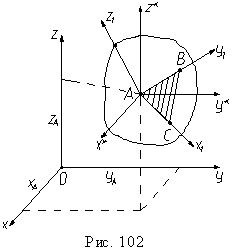 пределим
положение свободного твердого тела в
неподвижной системе координат Oxyz
следующим образом. Положение точки A
тела, которую назовем полюсом, определим
тремя ее координатами xA,
yA, zA (рис.
102). С полюсом свяжем начало базовой
системы координат Ax*y*z*, оси которой
при движении тела всегда остаются
параллельными осям неподвижной системы
координат. Точка A неподвижна в
базовой системе координат. Поэтому, как
и при сферическом движении, положение
треугольника ABC и тела в базовой
системе координат определим, например,
тремя углами Эйлера ψ, θ φ, которые
определяют ориентацию системы координат
Ax1y1z1,
связанной с телом, в базовой системе
координат. Таким образом, мы задали
движение свободного твердого тела
шестью независимыми между собой
параметрами, число которых, естественно,
совпадает с числом степеней свободы.
пределим
положение свободного твердого тела в
неподвижной системе координат Oxyz
следующим образом. Положение точки A
тела, которую назовем полюсом, определим
тремя ее координатами xA,
yA, zA (рис.
102). С полюсом свяжем начало базовой
системы координат Ax*y*z*, оси которой
при движении тела всегда остаются
параллельными осям неподвижной системы
координат. Точка A неподвижна в
базовой системе координат. Поэтому, как
и при сферическом движении, положение
треугольника ABC и тела в базовой
системе координат определим, например,
тремя углами Эйлера ψ, θ φ, которые
определяют ориентацию системы координат
Ax1y1z1,
связанной с телом, в базовой системе
координат. Таким образом, мы задали
движение свободного твердого тела
шестью независимыми между собой
параметрами, число которых, естественно,
совпадает с числом степеней свободы.
При движении тела эти шесть параметров изменяются с течением времени:
xA = xA(t), yA = yA(t), zA = zA(t), ψA = ψA(t), θA = θA(t), φA = φA(t) |
(1) |
Выражения (1) являются кинематическими уравнениями движения свободного твердого тела. Первые три из них описывают движение полюса A и поступательное движение базовой системы координат. Три последних уравнения описывают сферическое движение тела в базовой системе координат.
То есть движение свободного твердого тела состоит из поступательного движения совместно с полюсом и сферического движения вокруг полюса, которое часто называют угловым движением вокруг полюса или просто вращением вокруг полюса.
Нетрудно
доказать, что параметры сферического
движения не зависят от поступательного
движения. Для этого выберем новый полюс
A', из-за чего изменятся параметры
поступательного движения - траектория,
скорость, и ускорение полюса, так как
xA'
![]() xA,
yA'
yA,
zA'
zA.
А так как две другие точки B' и C'
кинематической модели твердого тела
выбираются произвольно, мы всегда можем
выбрать их так, чтобы оси новой связанной
системы координат Ax'1y'1z'1
были параллельны осям системы координат
Ax1y1z1
(на рис. 102 новая связанная система
координат и A' не показаны). Тогда
ψ' = ψ; θ' = θ; φ' = φ и параметры
сферического движения - угловая
ориентация, угловая скорость и угловое
ускорение - не изменятся.
xA,
yA'
yA,
zA'
zA.
А так как две другие точки B' и C'
кинематической модели твердого тела
выбираются произвольно, мы всегда можем
выбрать их так, чтобы оси новой связанной
системы координат Ax'1y'1z'1
были параллельны осям системы координат
Ax1y1z1
(на рис. 102 новая связанная система
координат и A' не показаны). Тогда
ψ' = ψ; θ' = θ; φ' = φ и параметры
сферического движения - угловая
ориентация, угловая скорость и угловое
ускорение - не изменятся.
Таким образом, движение свободного твердого тела состоит из поступательного движения совместно с полюсом и сферического движения вокруг полюса, которое не зависит от поступательного движения.
Мы сформулировали основное свойство движения свободного твердого тела, которое широко используется в управлении различными подвижными объектами. Навигационные системы управляют движением полюса (обычно за полюс выбирают центр масс), а системы ориентации управляют сферическим движением объекта. Наиболее четко такое разделение существует у космических аппаратов, которые находятся в безвоздушном пространстве и очень близки к свободному твердому телу. У кораблей, самолетов и ракет, двигающихся в воде или в воздухе, влияние обоих движений друг на друга больше из-за действия окружающей среды.
Также отметим, что базовую систему координат на борту объекта строят различные гироскопические приборы и системы, они же измеряют углы отклонения от нее и угловую скорость, которые используются для управления ориентацией объекта.

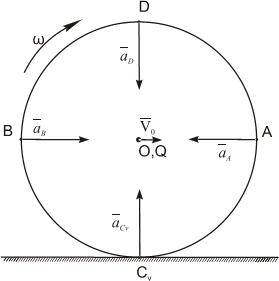 Рис.
1.13а
Рис.
1.13а