
- •Движение свободного твердого тела.
- •Задание движения свободного твердого тела.
- •Скорости и ускорения точек свободного твердого тела.
- •17. Основные аксиомы статики. Сложение сходящихся сил.
- •2)Центр параллельных сил
- •2)Определение координат тяжести однородного тела
- •Теоретическая механика кинематика
- •1.2. Первая задача динамики свободной точки
- •1.3. Вторая задача динамики свободной точки
- •2) Импульс силы
Скорости и ускорения точек свободного твердого тела.
Определим положение точки B и полюса A в неподвижной системе координат радиус-векторами rB и rA. Положение точки B в базовой системе координат, двигающейся поступательно, определим радиус-вектором ρ. На рис. 103 мы видим, что
|
(2) |
Д ифференцируя
по времени (2), учитывая формулу Эйлера,
имеем
ифференцируя
по времени (2), учитывая формулу Эйлера,
имеем
|
(3) |
где VBA - скорость вращения точки B вокруг полюса A, равная
|
(4) |
где
ω - угловая скорость вращения
радиус-вектора ρ и твердого тела
в базовой, а, следовательно, и в неподвижной
системе координат. Дифференцируя по
времени выражение VB
= VA + ω
 ρ,
получаем
ρ,
получаем
|
(5) |
где aBA - ускорение вращения точки B вокруг полюса A; aεBA - вращательное, а aωBA - осестремительное ускорения вращения точки B вокруг полюса A, которые выражаются так:
|
(6) |
В выражении (6) ε - угловое ускорение твердого тела в базовой, а следовательно, и в неподвижной системе координат.
Так, мы получили векторные выражения скорости и ускорения точки B, которые можно применять для нахождения скоростей и ускорений любых точек свободного твердого тела. Эти выражения, естественно, показывают, что скорости и ускорения точек тела состоят из скоростей и ускорений поступательного движения совместно с полюсом и скоростей и ускорений вращения точек тела в сферическом движении вокруг полюса.
ВИНТОВОЕ
ДВИЖЕНИЕ - движение твёрдого тела,
слагающееся из прямолинейного
поступательного
движения с нек-рой скоростью![]() и
вращательного
движения с нек-рой угловой
скоростью
и
вращательного
движения с нек-рой угловой
скоростью
![]() вокруг
оси аa1, параллельной направлению
постулат. скорости (рис. 1). Тело, совершающее
стационарное В. д., т. е. В. д., при к-ром
направление оси aa1
остаётся неизменным, наз. винтом; ось
аа1 наз. осью винта;
расстояние, проходимое любой точкой
тела, лежащей на оси аa1, за
время одного оборота, наз. шагом h
винта, величина
вокруг
оси аa1, параллельной направлению
постулат. скорости (рис. 1). Тело, совершающее
стационарное В. д., т. е. В. д., при к-ром
направление оси aa1
остаётся неизменным, наз. винтом; ось
аа1 наз. осью винта;
расстояние, проходимое любой точкой
тела, лежащей на оси аa1, за
время одного оборота, наз. шагом h
винта, величина
![]() -
параметром винта. Если вектор
-
параметром винта. Если вектор
![]() направлен
в сторону, откуда вращение тела видно
происходящим против хода часовой
стрелки, то при векторах
направлен
в сторону, откуда вращение тела видно
происходящим против хода часовой
стрелки, то при векторах
![]() ,
направленных в одну сторону, винт наз.
правым, а в разные стороны,- левым.
,
направленных в одну сторону, винт наз.
правым, а в разные стороны,- левым.
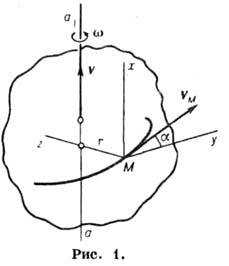
Скорость и ускорение любой точки M тела, отстоящей от оси аa1 на расстоянии r, численно равны
![]()
где
![]()
Когда
параметр р постоянен, шаг винта![]()
![]() также
постоянен. В этом случае всякая точка
M тела, не лежащая на оси aa1,
описывает винтовую линию, касательная
к к-рой в любой точке образует с плоскостью
yz, перпендикулярной оси aa1,
угол
также
постоянен. В этом случае всякая точка
M тела, не лежащая на оси aa1,
описывает винтовую линию, касательная
к к-рой в любой точке образует с плоскостью
yz, перпендикулярной оси aa1,
угол
![]()
![]() Любое
сложное движение твёрдого тела слагается
в общем случае из серии элементарных
или мгновенных В. д. Ось мгновенного В.
д. наз. мгновенной винтовой осью. В
отличие от оси стационарного В. д.,
мгновенная винтовая ось непрерывно
изменяет своё положение как по отношению
к системе отсчёта, в к-рой рассматривается
движение тела, так и по отношению к
самому телу, образуя при этом 2 линейчатые
(соприкасающиеся но прямой линии)
поверхности, наз. соответственно
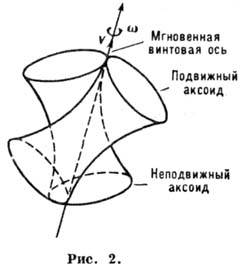
неподвижным и подвижным аксоидами (рис.
2). Геом. картину движения тела можно в
общем случае получить качением с
продольным проскальзыванием подвижного
аксоида по неподвижному, осуществляя
таким путём серию тех последоват. В. д.,
из к-рых слагается движение тела.
Любое
сложное движение твёрдого тела слагается
в общем случае из серии элементарных
или мгновенных В. д. Ось мгновенного В.
д. наз. мгновенной винтовой осью. В
отличие от оси стационарного В. д.,
мгновенная винтовая ось непрерывно
изменяет своё положение как по отношению
к системе отсчёта, в к-рой рассматривается
движение тела, так и по отношению к
самому телу, образуя при этом 2 линейчатые
(соприкасающиеся но прямой линии)
поверхности, наз. соответственно
неподвижным и подвижным аксоидами (рис.
2). Геом. картину движения тела можно в
общем случае получить качением с
продольным проскальзыванием подвижного
аксоида по неподвижному, осуществляя
таким путём серию тех последоват. В. д.,
из к-рых слагается движение тела.
№13.Полная и локальная производная вектора. Теорема о сложении скоростей точки.
Теорема о сложении скоростей.
При сложном движении точки абсолютная скорость равна сумме ее относительной и переносной скоростей.
 .
.
Доказательство.
В каждый момент времени справедливo
равенство:
![]() .
.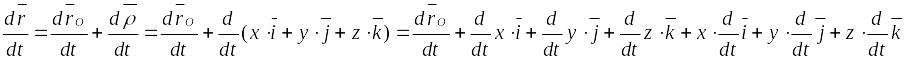
По
формуле Эйлера
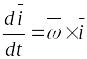 ,
,
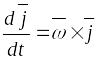 ,
,
![]()
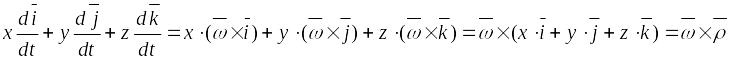
![]()
![]()

![]()
В
это выражение входит переносная
скорость
![]()
Окончательно
имеем
![]()
Применяя
полученную формулу отдельно для
вектора
![]() ,
запишем
,
запишем
![]() Эта формула выражает абсолютную
производную любого вектора с помощью
относительной производной и движение
подвижной системы координат с угловой
скоростью
Эта формула выражает абсолютную
производную любого вектора с помощью
относительной производной и движение
подвижной системы координат с угловой
скоростью
![]() (Формула Бура) .
(Формула Бура) .
![]() .
.
Полная и локальная производные вектора. Формула Бура.
Рассмотрим изменение вектора b(t) по отношению к двум системам координат — подвижной O'XYZ и неподвижной Oxyz.

Абсолютной,
или полной,
производной вектора b по аргументу t
назьшается вектор
![]() определяющий
изменение вектоpa b(t) в неподвижной
системе Oxyz.
определяющий
изменение вектоpa b(t) в неподвижной
системе Oxyz.
Относительная,
или локальная,
производная
![]() определяет
измененине вектора b(t) в подвижной
системе O'XYZ.
определяет
измененине вектора b(t) в подвижной
системе O'XYZ.
Формула
Бура
(получается из зависимости между полной
и локальной производными):
 .
.
Рассомтрим частные случаи.
1) угловая скорость = 0, то = ;
2)
вектор b не меняется в подвижной системе
отсчета (
=0),
то
 ;
;
3)
![]() ,
т.е. вектор b все время параллелен вектору
угловой скорости (
,
т.е. вектор b все время параллелен вектору
угловой скорости (![]() ),
то
=
.
В частности, если
),
то
=
.
В частности, если
![]() ,
то
,
то
![]() ,
т.е. вектор угловой скорости изменяется
одинаково для подвижной и неподвижной
систем координат.
,
т.е. вектор угловой скорости изменяется
одинаково для подвижной и неподвижной
систем координат.
Дополнение:
Выведение формулы Бура:
Найдем
зависимость между полной и локальными
производными. Если воспользоваться
проекциями вектора b(t) на оси подвижной
системы O'XYZ, то можно записать:![]() ,
где I, J, К — орты, не изменяемые в этой
системе отсчета. Поэтому локальная
производная
,
где I, J, К — орты, не изменяемые в этой
системе отсчета. Поэтому локальная
производная
 ,
а полная производная
с
учетом изменения также ортов I, J , К имеет
вид:
,
а полная производная
с
учетом изменения также ортов I, J , К имеет
вид:
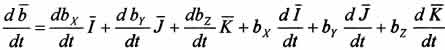 .
В правой части уравнения первые три
слагаемых выражают локальную производную,
а производные от ортов I, J, K определяются
формулами Пуассона (
.
В правой части уравнения первые три
слагаемых выражают локальную производную,
а производные от ортов I, J, K определяются
формулами Пуассона (![]() ),
т.е.
),
т.е.
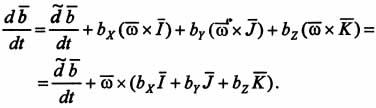 .
С учетом
получаем:
.
.
С учетом
получаем:
.
14.
Теория сложения ускорений точки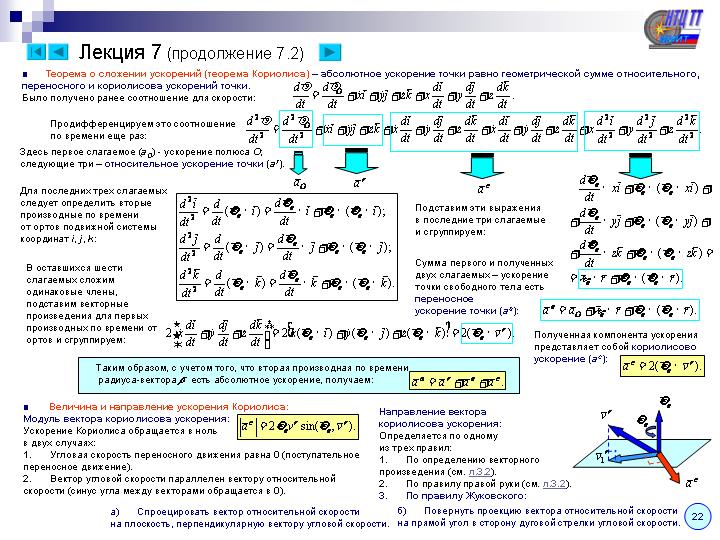
 2
2
3
16.
 2
2
3
