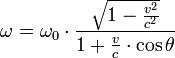- •2.Билет
- •3.Билет
- •4.Билет.
- •5 Билет.
- •6.Билет
- •7.Билет
- •8.Билет
- •10 Билет
- •11.Билет
- •12 Билет
- •13 Билет
- •14 Билет
- •15 Билет
- •16Билет
- •17.Билет
- •18.Билет
- •19.Билет
- •20.Билет
- •21Билет
- •22Билет
- •23 Билет
- •25 Билет
- •26 Билет
- •28.Билет
- •29 Билет
- •41. Вихревое электрическое поле
- •42. Дифференциальная и интегральная формы уравнений Максвелла.
- •43. Колебательный процесс. Виды колебаний . Гармонические колебания и их параметры.
- •44. Дифференциальное уравнение гармонических колебаний. Энергия гарм.Колеб.
- •45.Линейный гармонический Осциллятор, Математический и физический маятники:
- •46.Сложение одинаково направленных гармонических колебаний, биения.
- •47.Сложение взаимно перпендикулярных колебаний. Фигуры Лиссажу. Физический смысл спектрального разложения.
- •48.Свободно затухающие колебания. Дифференциальное уравнение свободных затухающих колебаний
- •50 Вопрос
- •51 Вопрос
- •52 Вопрос
52 Вопрос
Переме́нный ток, AC (англ. alternating current — переменный ток) — электрический ток, который периодически изменяется по модулю и направлению.
Под переменным током также подразумевают ток в обычных одно- и трёхфазных сетях. В этом случае мгновенные значения тока и напряжения изменяются по гармоническому закону. В устройствах-потребителях постоянного тока переменный ток часто преобразуется выпрямителями для получения постоянного тока.
Переменный ток получают путем вращения рамки в магнитном поле. Принцип действия — явление электромагнитной индукции (появление индукционного тока в замкнутом контуре при изменении магнитного потока). В генераторах переменного тока вращается якорь из магнита (электромагнита) с несколькими полюсами (2, 4, 6 и т. д.), а с обмоток статора снимается переменное напряжение.
Рассмотрим последовательно процессы, происходящие на участке цепи, содержащем резистор, катушку индуктивности и конденсатор, к концам которого приложено переменное напряжение
![]()
где Um — амплитуда напряжения
 рис
215
рис
215
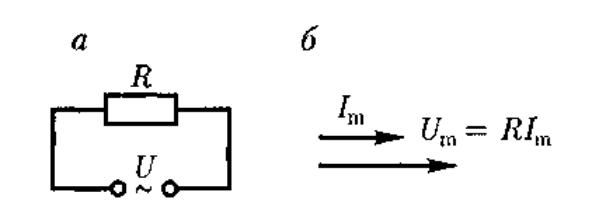
1. Переменный ток, текущий через резистор сопротивлением R (L —• О, С—> 0) (рис. 215, а). При выполнении условия квазистационарности ток через резистор определяется законом Ома: где амплитуда силы тока / т = Для наглядного изображения соотношений между переменными токами и напряжениями воспользуемся jwemo-дом векторных диаграмм. На рис. 215,6 дана векторная диаграмма амплитудных значений тока /|п и напряжения Um на резисторе (сдвиг фаз между /ш и Um равен нулю).
2. Переменный ток, текущий через катушку индуктивностью L (R -> 0, С—≫ 0) (рис. 216, а). Если в цепи приложено переменное напряжение то в ней потечет переменный ток, в результате чего возникнет ЭДС самоиндукции ≪fs = —L— . Тогда закон Ома для рассматриваемого участка цепи имеет вид
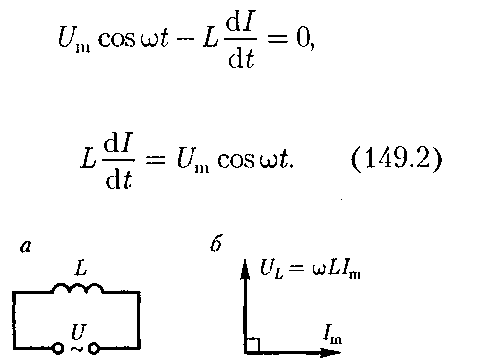
 Рис.216
Рис.216
Так как внешнее напряжение приложено к катушке индуктивности, то
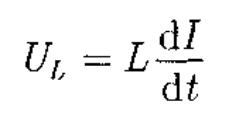 (149.3)
(149.3)
есть падение напряжения на катушке. Из уравнения (149.2) следует, что После интегрирования, учитывая, что
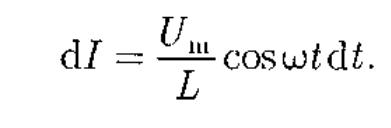
постоянная интегрирования равна нулю (так как отсутствует постоянная составляющая тока), получим
![]()
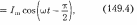
где /In =![]()
Величина RL
=![]()
![]() (149.5) называется
реактивным
индуктивным сопротивлением (или
индуктивным
сопротивлением). Из
выражения (149.5)
вытекает, что для постоянного
тока
(149.5) называется
реактивным
индуктивным сопротивлением (или
индуктивным
сопротивлением). Из
выражения (149.5)
вытекает, что для постоянного
тока
(омега = 0) катушка
индуктивности не
имеет сопротивления.
Подстановка значения Um
=![]() в выражение
(149.2) с
учетом (149.3) приводит к следующему
значению падения напряжения на
в выражение
(149.2) с
учетом (149.3) приводит к следующему
значению падения напряжения на
катушке индуктивности:
![]() (149.6) Сравнение
выражений (149.4) и (149.6) приводит к выводу,
что падение напряжения UL
опережает по фазе
ток I, текущий через катушку, на (пи/2),
что и показано на векторной диаграмме
(рис. 216,б).
(149.6) Сравнение
выражений (149.4) и (149.6) приводит к выводу,
что падение напряжения UL
опережает по фазе
ток I, текущий через катушку, на (пи/2),
что и показано на векторной диаграмме
(рис. 216,б).
3. Переменный ток, текущий через конденсатор емкостью С (R —> 0, L —> 0) (рис. 217, а). Если переменное напряжение (149.1) приложено к конденсатору, то он все время перезаряжается, и в цепи течет переменный ток. Так как все внешнее напряжение приложено к конденсатору, а сопротивлением подводящих проводов можно пренебречь, то
![]()
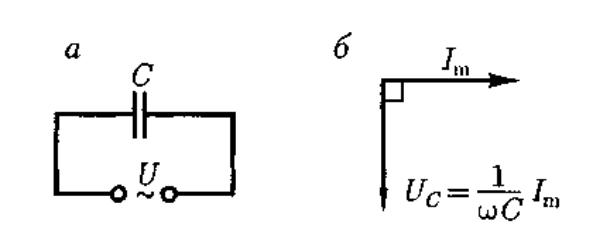 рис
217
рис
217
Сила тока

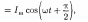 (149.7)
(149.7)
![]() а
а
![]() называется
реактивным
емкостным
называется
реактивным
емкостным
сопротивлением (или емкостным сопротивлением). Для постоянного тока (ш = 0) Rc = оо, т. е. постоянный ток через конденсатор течь не может. Падение напряжения на конденсаторе
![]() (149.8) Сравнение
выражений (149.7) и (149.8) приводит к выводу,
что падение напряжения Uc
отстает по фазе
от текущего через конденсатор тока I
на (пи/2).
(149.8) Сравнение
выражений (149.7) и (149.8) приводит к выводу,
что падение напряжения Uc
отстает по фазе
от текущего через конденсатор тока I
на (пи/2).
Это показано на векторной диаграмме (рис. 217, б).
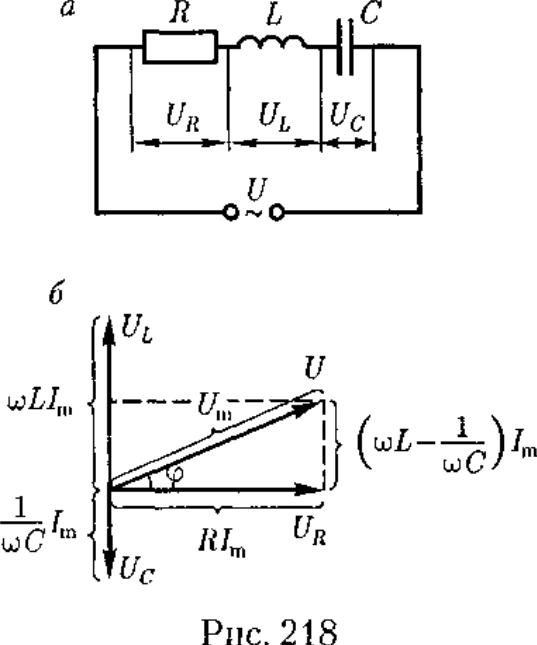
4. Цепь переменного тока, содержащая последовательно включенные резистор, катушку индуктивности и конденсатор. На рис. 218, а представлен участок цепи, содержащий резистор
сопротивлением R, катушку индуктивностью L и конденсатор емкостью С, к концам которого приложено переменное напряжение (149.1). В цепи возникнет переменный ток, который вызовет на всех элементах цепи соответствующие падения напряжения UR, UL и Uc.
На рис. 218,6 представлена векторная диаграмма амплитуд падений напряжений на резисторе ( UR), катушке ( UL) и конденсаторе ( Uc). Амплитуда Um приложенного напряжения должна быть равна векторной сумме амплитуд этих падений напряжений. Как видно из рис. 218, б, угол ф определяет разность фаз между напряжением и силой тока. Из рисунка следует, что
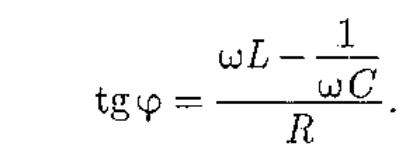 (149.9)
Из прямоугольного треугольника
полу-
(149.9)
Из прямоугольного треугольника
полу-![]() откуда
амплитуда силы тока имеет значение
откуда
амплитуда силы тока имеет значение
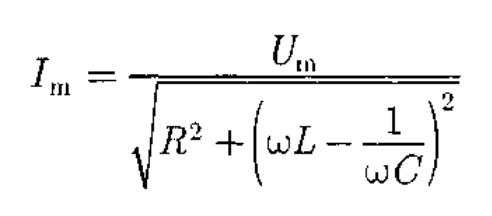 (149.10)
Следовательно, если напряжение в цепи
изменяется по закону U
= Umcos
(149.10)
Следовательно, если напряжение в цепи
изменяется по закону U
= Umcos![]() t,
то в цепи течет
ток
t,
то в цепи течет
ток
![]() (149.11)
(149.11)
 где
фи и Im определяются соответственно
формулами (149.9) и (149.10). Величина
где
фи и Im определяются соответственно
формулами (149.9) и (149.10). Величина
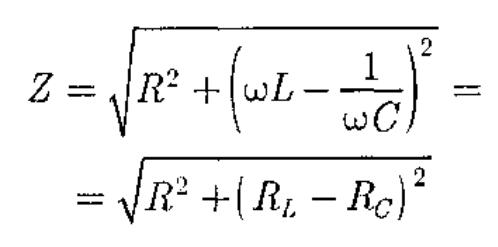 (149.12)
называется полным
сопротивлением цепи,
а величина
(149.12)
называется полным
сопротивлением цепи,
а величина![]() —
реактивным
сопротивлением.
—
реактивным
сопротивлением.
Рассмотрим частный случай, когда в цепи отсутствует конденсатор. В данном случае падения напряжений UR и UL в сумме равны приложенному напряжению U. Векторная диаграмма для
данного случая представлена на рис. 219, из которого следует, что
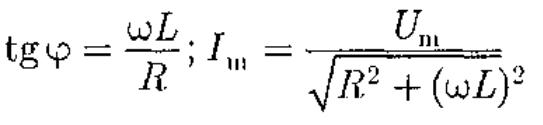 (149.13)
(149.13)
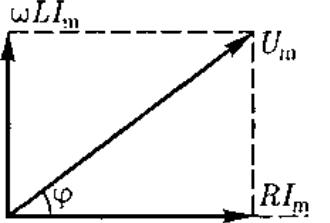 рис 219
рис 219
Выражения (149.9) и
(149.10) совпадают с (149.13), если в них![]() =
0, т.е. С=
бесконечности.
Следовательно, отсутствие конденсатора
в цепи означает, что С=
бесконечности, а
не С= 0.
Данный вывод можно трактовать следующим
образом: сближая обкладки конденсатора
до их полного соприкосновения, получим
цепь, в которой конденсатор отсутствует
расстояние между обкладками стремится
к нулю, а емкость — к бесконечности.
=
0, т.е. С=
бесконечности.
Следовательно, отсутствие конденсатора
в цепи означает, что С=
бесконечности, а
не С= 0.
Данный вывод можно трактовать следующим
образом: сближая обкладки конденсатора
до их полного соприкосновения, получим
цепь, в которой конденсатор отсутствует
расстояние между обкладками стремится
к нулю, а емкость — к бесконечности.
53 вопрос
Волны - это изменение состояния среды (возмущения), распространяющиеся в этой среде и несущие с собой энергию и импульс без переноса вещества. Наиболее часто встречающиеся виды волн — упругие (звук) и электромагнитные (свет, радиоволны и другие).
Примером волнового движения может быть возмущение воды от падающих капель, которое распространяется в виде расширяющихся концентрических кругов.
Волновое уравнение: A = A0 cos(ωt + kx)
Волновое уравнение описывает распространение гармонических колебаний в пространстве. Характерными параметрами, описывающими гармоническую волну являются: A0 - амплитуда колебаний; ω - круговая частота (рад/с); период колебаний T (с), который связан с круговой частотой соотношением: T = 2π/ω; частота колебаний γ (Гц = 1/с) выражается через период: γ = 1/T; волновое число k = ω/v (где v- скорость распространения волны, измеряется в м/с); λ - длина (м) волны (λ = vT). Скорость распространения каждого вида волн зависит от свойств среды, в которой они распространяются. Если колебания совершаются поперек по отношению к направлению распространения волн, они называются поперечными, если вдоль - продольными.
Поперечные волны могут возникать в твердых телах. Электромагнитные волны, в том числе и свет, являются поперечными. Продольные волны могут возникать, как в твердых телах, так и в жидкостях и газах.
В общем случае волновое уравнение записывается в виде
![]() ,
,
где
![]() —
оператор
Лапласа,
—
оператор
Лапласа,
![]() —
неизвестная функция,
—
неизвестная функция,
![]() —
время,
—
время,
![]() —
пространственная переменная,
—
пространственная переменная,
![]() —
фазовая
скорость.
—
фазовая
скорость.
Волновой вектор — вектор, направление которого перпендикулярно фазовому фронту бегущей волны, а абсолютное значение равно волновому числу.
Волновой вектор обычно
обозначается латинской буквой
![]() и
величина его измеряется в обратных
метрах (СИ)
или обратных сантиметрах (СГС)
(т.е. радианах на метр или радианах на
сантиметр). (Следует быть внимательным,
т.к. иногда может использоваться
определение, отличающееся множителем
и
величина его измеряется в обратных
метрах (СИ)
или обратных сантиметрах (СГС)
(т.е. радианах на метр или радианах на
сантиметр). (Следует быть внимательным,
т.к. иногда может использоваться
определение, отличающееся множителем
![]() ,
но дающее ту же физическую размерность).
,
но дающее ту же физическую размерность).
Волновое число связано
с длиной
волны λ
соотношением:
![]()
.Связь между волновым вектором и частотой задаётся законом дисперсии. Все возможные значения волновых векторов образуют обратное пространство или k-пространство.
Наиболее общим определением волнового вектора можно считать такое: волновой вектор есть градиент фазы волны:
![]()
Выведем уравнение волны, которое позволит определить смещение каждой точки среды в любой момент времени при распространении гармонической волны.
Сделаем это на примере волны, бегущей по длинному тонкому резиновому шнуру.
Ось ОХ направим вдоль
шнура, а начало отсчета свяжем с левым
концом шнура. Смещение колеблющейся
точки шнура от положения равновесия
обозначим буквой s. Для описания волнового
процесса нужно знать смещение каждой
точки шнура в любой момент времени.
Следовательно, надо знать вид функции
S = s(x, t).
Заставим конец шнура (точка
с координатой х = 0) совершать гармонические
колебания с циклической частотой (0.
Колебания этой точки будут происходить
по закону: s = sm sin
![]() t,
(6.3)
t,
(6.3)
Колебания распространяются
вдоль шнура (оси ОХ) со cкоростью
![]() и
в произвольную точку шнура с координатой
и
в произвольную точку шнура с координатой
![]() прийдут
спустя время
прийдут
спустя время

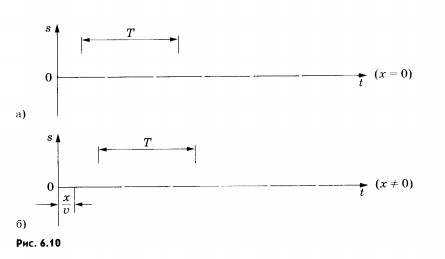 Эта
точка также начнет совершать гармонические
колебания с частотой
,
но с запаздыванием на время
(рис. 6.10, б). Если пренебречь затуханием
волны по мере ее распространения, то
колебания в точке х будут происходить
с той же амплитудой sm, но с другой
фазой:
Эта
точка также начнет совершать гармонические
колебания с частотой
,
но с запаздыванием на время
(рис. 6.10, б). Если пренебречь затуханием
волны по мере ее распространения, то
колебания в точке х будут происходить
с той же амплитудой sm, но с другой
фазой:
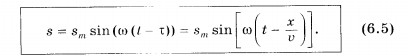 Это
и есть уравнение гармонической бегущей
волны, распространяющейся в положительном
направлении оси Ох.
Это
и есть уравнение гармонической бегущей
волны, распространяющейся в положительном
направлении оси Ох.
54 вопрос
55 вопрос
Частным случаем интерференции являются стоячие волны — это волны, образующиеся при наложении двух бегущих волн, распространяющихся навстречу друг другу с одинаковыми час-
тотами и амплитудами, а в случае поперечных волн еще и одинаковой поляризацией.
Для вывода уравнения стоячей волны предположим, что две плоские волны распространяются навстречу друг другу вдоль оси ж в среде без затухания, причем обе волны характеризуются одинаковыми амплитудами и частотами. Кроме того, начало координат вы-
берем в точке, в которой обе волны имеют одинаковую начальную фазу, а отсчет времени начнем с момента, когда начальные фазы обеих волн равны нулю. Тогда соответственно уравнения волны, распространяющейся вдоль положительного направления оси х, и волны, распространяющейся ей навстречу, будут иметь вид
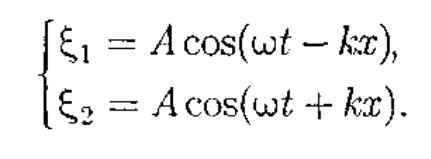 (157.1)
(157.1)
k=2пи./ лямбда,
следовательно уравнение стоячей волны:
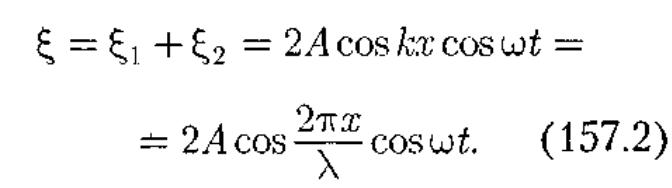
Из уравнения стоячей
волны (157.2) вытекает, что в каждой точке
этой волны происходят колебания той же
частоты омега с амплитудой АСТ
=модуль(![]() ),
зависящей от координаты х
рассматриваемой
точки.
),
зависящей от координаты х
рассматриваемой
точки.
В точках среды, где
![]() m=0,1,2… (157.3)
m=0,1,2… (157.3)
амплитуда колебаний достигает максимального значения, равного 2А. В точках среды, где
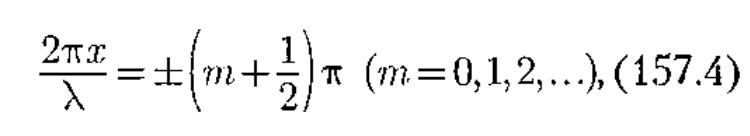 амплитуда
колебаний обращается в
амплитуда
колебаний обращается в
нуль. Точки, в которых амплитуда колебаний максимальна (Acr ~ 2А), называются пучностями стоячей волны, а точки, в которых амплитуда колебаний равна нулю (Ап. — 0), называются уз-
лами стоячей волны. Точки среды, находящиеся в узлах, колебаний не совершают. Из выражений (157.3) и (157.4) получим соответственно координаты пучностей и узлов:
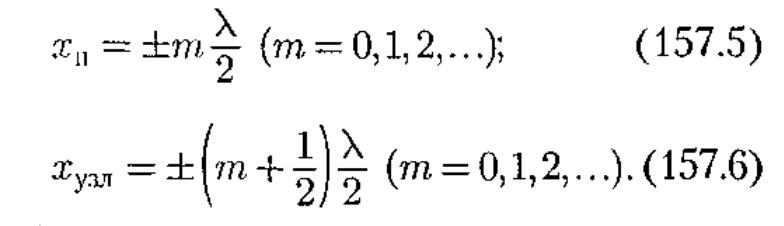
Из формул (157.5) и (157.6)
следует, что расстояния между двумя
соседними пучностями и двумя соседними
узлами одинаковы и равны
(лямбда/2). Расстояние
между соседними пучностью и узлом
стоячей волны равно (лямбда/4).
В отличие от
бегущей волны, все
точки которой
совершают колебания с одинаковой
амплитудой, но с
запаздыванием по
фазе . все точки
стоячей волны между двумя узлами
колеблются с
разными амплитудами, но
с одинаковыми
фазами . При
переходе через узел множитель 2
A cos
![]() меняет
свой знак, поэтому фаза колебаний по
разные стороны от узла отличается на
(пи), т. е. точки, лежащие по разные стороны
от узла, колеблются в противофазе.
Образование стоячих волн наблюдают при
интерференции бегущей и отраженной
волн. Если конец веревки закрепить
неподвижно (например, к стене), то
отраженная в месте закрепления веревки
волна будет интерферировать с бегущей
волной, образуя стоячую волну .На границе,
где происходит отражение волны, в данном
случае возникает узел. Будет ли на
границе отражения узел
меняет
свой знак, поэтому фаза колебаний по
разные стороны от узла отличается на
(пи), т. е. точки, лежащие по разные стороны
от узла, колеблются в противофазе.
Образование стоячих волн наблюдают при
интерференции бегущей и отраженной
волн. Если конец веревки закрепить
неподвижно (например, к стене), то
отраженная в месте закрепления веревки
волна будет интерферировать с бегущей
волной, образуя стоячую волну .На границе,
где происходит отражение волны, в данном
случае возникает узел. Будет ли на
границе отражения узел
или пучность, зависит от соотношения плотностей сред. Если среда, от которой происходит отражение, менее плотная, то в месте отражения возникает пучность (рис. 224, а), если более плотная — узел (рис. 224, б). Образование узла связано с тем, что волна, отражаясь от более плотной среды, меняет фазу на противоположную и у границы происходит сложение колебаний с противоположными фазами, в результате чего получается узел.
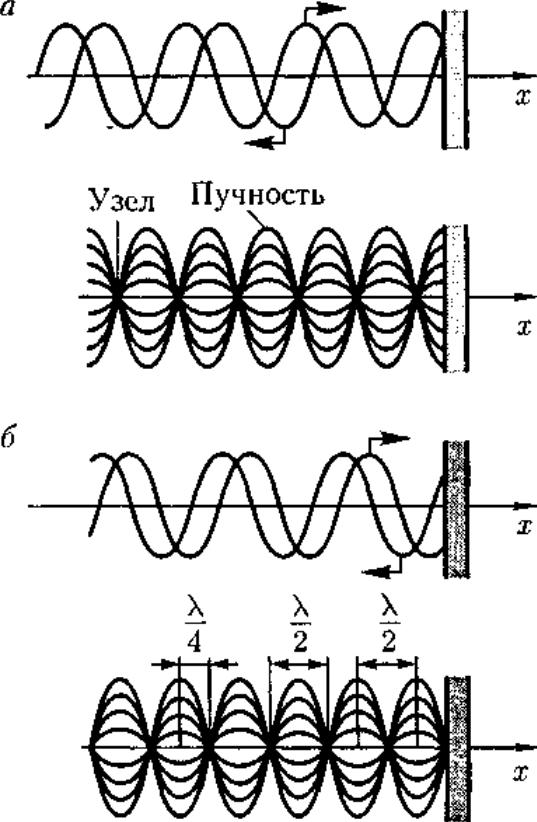 рис 224
рис 224
56 вопрос
Аку́стика (от греч. ἀκούω (аку́о) — слышу) — наука о звуке, изучающая физическую природу звука и проблемы, связанные с его возникновением, распространением, восприятием и воздействием. Акустика является одним из направлений физики (механики), исследующих упругие колебания и волны от самых низких (условно от 0 Гц) до высоких частот.
57 вопрос
Эффектом Доплера* называется изменение частоты колебаний, воспринимаемой приемником, при движении источника этих колебаний и приемника друг относительно друга. Например, из опыта известно, что тон гудка поезда повышается по мере его приближения к платформе и понижается при удалении, т. е. движение источника колебаний (гудка) относительно приемника (уха) изменяет частоту принимаемых колебаний.
* X. Доплер (1803—1853) — австрийский физик, математик и астроном.
Для рассмотрения эффекта Доплера предположим, что источник и приемник звука движутся вдоль соединяющей их прямой; vист и vпр — соответственно скорости движения источника и приемника, причем они положительны, если источник (приемник) приближается к приемнику (источнику), и отрицательны, если удаляется. Частота колебаний источника равна v0.
1. Источник и приемник покоятся относительно среды, т. е. vист = vпр=0. Если v — скорость распространения звуковой волны в рассматриваемой среде, то длина волны =vT=v/v0. Распространяясь в среде, волна достигнет приемника и вызовет колебания его звукочувствительного элемента с частотой
![]()
Следовательно, частота v звука, которую зарегистрирует приемник, равна частоте v0, с которой звуковая волна излучается источником.
2. Приемник приближается к источнику, а источник покоится, т. е. vпр>0, vист=0. В данном случае скорость распространения волны относительно приемника станет равной v + vпр. Так как длина волны при этом не меняется, то
![]()
т. е. частота колебаний, воспринимаемых приемником, в (v+vпр)/v раз больше частоты колебаний источника.
3. Источник приближается к преемнику, а приемник покоится, т. е. vист >0, vпр=0.
Скорость распространения колебаний зависит лишь от свойств среды, поэтому за время, равное периоду колебаний источника, излученная им волна пройдет в направлении к приемнику расстояние vT (равное длине волны ) независимо от того, движется ли источник или покоится. За это же время источник пройдет в направлении волны расстояние vистT (рис. 224), т. е. длина волны в направлении движения сократится и станет равной '=—vистТ=(v—vист)T, тогда
![]()
т. е. частота колебаний, воспринимаемых приемником, увеличится в v/(v – vист) раз. В случаях 2 и 3, если vист<0 и vпр<0, знак будет обратным.
4. Источник и приемник движутся относительно друг друга. Используя результаты, полученные для случаев 2 и 3, можно записать выражение для частоты колебаний, воспринимаемых приемником:
![]() (159.1)
(159.1)
причем верхний знак берется, если при движении источника или приемника происходит их сближение, нижний знак — в случае их взаимного удаления.
Из приведенных формул следует, что эффект Доплера различен в зависимости от того, движется ли источник или приемник. Если направления скоростей vпр и vист не совпадают с проходящей через источник и приемник прямой, то вместо этих скоростей в формуле (159.1) надо брать их проекции на направление этой прямой.
58 вопрос
Существование электромагнитных волн было теоретически предсказано великим английским физиком Дж. Максвеллом в 1864 году. Максвелл проанализировал все известные к тому времени законы электродинамики и сделал попытку применить их к изменяющимся во времени электрическому и магнитному полям. Он обратил внимание на ассиметрию взаимосвязи между электрическими и магнитными явлениями. Максвелл ввел в физику понятие вихревого электрического поля и предложил новую трактовку закона электромагнитной индукции, открытой Фарадеем в 1831 г.:
Всякое изменение магнитного поля порождает в окружающем пространстве вихревое электрическое поле, силовые линии которого замкнуты.
Максвелл высказал гипотезу о существовании и обратного процесса:
Изменяющееся во времени электрическое поле порождает в окружающем пространстве магнитное поле.
Рис. 2.6.1 и 2.6.2 иллюстрируют взаимное превращение электрического и магнитного полей.
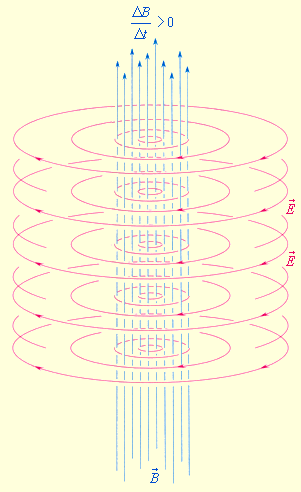
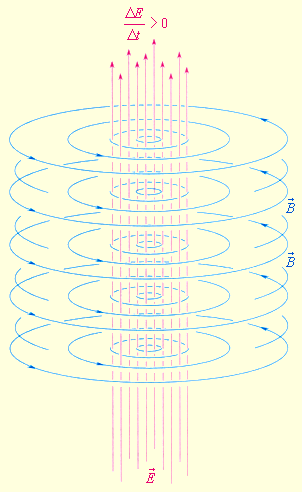
Рис 2.6.1. Рис 2.6.2
Закон электромагнитной Гипотеза Максвелла. Изменяющееся эл. поле
индукции в трактовке Максвелла порождает магнитное
. Электромагнитные волны распространяются в веществе с конечной скоростью
|
Здесь ε и μ – диэлектрическая и магнитная проницаемости вещества, ε0 и μ0 – электрическая и магнитная постоянные: ε0 = 8,85419·10–12 Ф/м, μ0 = 1,25664·10–6 Гн/м.
Длина волны λ в синусоидальной волне свявзана со скоростью υ распространения волны соотношением λ = υT = υ / f, где f – частота колебаний электромагнитного поля, T = 1 / f.
Скорость электромагнитных волн в вакууме (ε = μ = 1):
|
Скорость c распространения электромагнитных волн в вакууме является одной из фундаментальных физических постоянных.
Вывод Максвелла о конечной скорости распространения электромагнитных волн находился в противоречии с принятой в то время теорией дальнодействия, в которой скорость распространения электрического и магнитного полей принималась бесконечно большой. Поэтому теорию Максвелла называют теорией близкодействия.
3. В электромагнитной волне происходят взаимные превращения электрического и магнитного полей. Эти процессы идут одновременно, и электрическое и магнитное поля выступают как равноправные «партнеры». Поэтому объемные плотности электрической и магнитной энергии равны друг другу: wэ = wм.
|
Отсюда следует, что
в электромагнитной волне модули индукции
магнитного поля
![]() и
напряженности электрического поля
и
напряженности электрического поля
![]() в
каждой точке пространства связаны
соотношением
в
каждой точке пространства связаны
соотношением
|
4. Электромагнитные волны переносят энергию. При распространении волн возникает поток электромагнитной энергии. Если выделить площадку S (рис. 2.6.3), ориентированную перпендикулярно направлению распространения волны, то за малое время Δt через площадку протечет энергия ΔWэм, равная
ΔWэм = (wэ + wм)υSΔt. |
Плотностью потока или интенсивностью I называют электромагнитную энергию, переносимую волной за единицу времени через поверхность единичной площади:
|
Подставляя сюда выражения для wэ, wм и υ, можно получить:
|
Поток энергии в
электромагнитной волне можно задавать
с помощью вектора
![]() направление
которого совпадает с направлением
распространения волны, а модуль равен
EB / μμ0. Этот вектор называют вектором
Пойнтинга.
направление
которого совпадает с направлением
распространения волны, а модуль равен
EB / μμ0. Этот вектор называют вектором
Пойнтинга.
В синусоидальной (гармонической) волне в вакууме среднее значение Iср плотности потока электромагнитной энергии равно
|
где E0 – амплитуда колебаний напряженности электрического поля.
Плотность потока энергии в СИ измеряется в ваттах на квадратный метр (Вт/м2).
Существование давления электромагнитных волн позволяет сделать вывод о том, что электромагнитному полю присущ механический импульс. Импульс электромагнитного поля в единичном объеме выражается соотношением
|
где wэм – объемная плотность электромагнитной энергии, c – скорость распространения волн в вакууме. Наличие электромагнитного импульса позволяет ввести понятие электромагнитной массы.
Для поля в единичном объеме
|
Отсюда следует:
|
Это соотношение между массой и энергией электромагнитного поля в единичном объеме является универсальным законом природы. Согласно специальной теории относительности, оно справедливо для любых тел независимо от их природы и внутреннего строения.
Как показывает опыт, электромагнитные волны могут производить различные действия: нагревание тел при поглощении света, вырывание электронов с поверхности металла под действием света (фотоэффект). Это свидетельствует о том, что электромагнитные волны переносят энергию. Эта энергия заключена в распространяющихся в пространстве электрическом и магнитном полях.
В курсе электричества и магнетизма было показано, что объемная плотность энергии электрического поля равна
|
(1.1) |
а магнитного поля –
|
(1.2) |
где
![]() и
и
![]() –
электрическая и магнитная постоянные.
Таким образом, полная плотность энергии
электромагнитной волны равна
–
электрическая и магнитная постоянные.
Таким образом, полная плотность энергии
электромагнитной волны равна
|
(1.3) |
Так как модули вектора
напряженности электрического и индукции
магнитного поля в электромагнитной
волне связаны соотношением
![]() ,
то полную энергию можно выразить только
через напряженность электрического
поля или индукцию магнитного поля:
,
то полную энергию можно выразить только
через напряженность электрического
поля или индукцию магнитного поля:
|
(1.4) |
Из (1.4) видно, что объемная плотность энергии складывается из двух равных по величине вкладов, соответствующих плотностям энергии электрического и магнитного полей. Это обусловлено тем, что в электромагнитной волне происходят взаимные превращения электрического и магнитного полей. Эти процессы идут одновременно, и электрическое и магнитное поля выступают как равноправные «партнеры».
Плотность энергии электромагнитного поля можно представить в виде:
|
(1.5) |
Формула (1.5) характеризует плотность энергии в любой момент времени в любой точке пространства.
Если выделить площадку
с площадью s, ориентированную перпендикулярно
направлению распространения волны, то
за малое время Δt через площадку пройдет
энергия
![]() ,
равная
,
равная
![]() где
где
![]() –
скорость электромагнитной волны в
вакууме.
–
скорость электромагнитной волны в
вакууме.
Вектор Пойнтинга (также вектор Умова — Пойнтинга) — вектор плотности потока энергии электромагнитного поля, одна из компонент тензора энергии-импульса электромагнитного поля. Вектор Пойнтинга S можно определить через векторное произведение двух векторов:
![]() (в
системе СГС),
(в
системе СГС),
![]() (в
системе СИ),
(в
системе СИ),
где E и H — векторы напряжённости электрического и магнитного полей соответственно.
![]() (в
комплексной форме),
(в
комплексной форме),
где E и H — векторы комплексной амплитуды электрического и магнитного полей соответственно.
Этот вектор по модулю равен количеству энергии, переносимой через единичную площадь, нормальную к S, в единицу времени. Своим направлением вектор определяет направление переноса энергии.Поскольку тангенциальные к границе раздела двух сред компоненты E и H непрерывны (см. граничные условия), то вектор S непрерывен на границе двух сред.
59 вопрос
Эффе́кт До́плера — изменение частоты и длины волн, регистрируемых приёмником, вызванное движением их источника и/или движением приёмника.
Если источник волн движется относительно среды, то расстояние между гребнями волн (длина волны) зависит от скорости и направления движения. Если источник движется по направлению к приёмнику, то есть догоняет испускаемую им волну, то длина волны уменьшается, если удаляется — длина волны увеличивается:
|
|
где
![]() —
частота, с которой источник испускает
волны,
—
частота, с которой источник испускает
волны,
![]() —
скорость распространения волн в среде,
—
скорость источника волн относительно
среды (положительная, если источник
приближается к приёмнику и отрицательная,
если удаляется).
—
скорость распространения волн в среде,
—
скорость источника волн относительно
среды (положительная, если источник
приближается к приёмнику и отрицательная,
если удаляется).
Частота, регистрируемая неподвижным приёмником
|
(1) |
Аналогично, если приёмник движется навстречу волнам, он регистрирует их гребни чаще и наоборот. Для неподвижного источника и движущегося приёмника
|
(2) |
где
![]() —
скорость приёмника относительно среды
(положительная, если он движется по
направлению к источнику).
—
скорость приёмника относительно среды
(положительная, если он движется по
направлению к источнику).
Подставив вместо
в
формуле (2) значение частоты
![]() из
формулы (1), получим формулу для общего
случая:
из
формулы (1), получим формулу для общего
случая:
|
В случае распространения электромагнитных волн (или других безмассовых частиц) в вакууме, формулу для частоты выводят из уравнений специальной теории относительности. Так как для распространения электромагнитных волн не требуется материальная среда, можно рассматривать только относительную скорость источника и наблюдателя[2][3].
|
|
где
—
скорость
света,
—
скорость источника относительно
приёмника (наблюдателя),
![]() —
угол между направлением на источник и
вектором скорости в системе отсчёта
приёмника. Если источник радиально
удаляется от наблюдателя, то
—
угол между направлением на источник и
вектором скорости в системе отсчёта
приёмника. Если источник радиально
удаляется от наблюдателя, то
![]() ,
если приближается —
,
если приближается —
![]() [4].
[4].

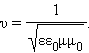
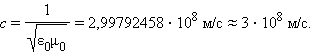
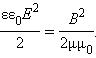
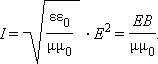
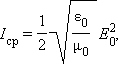
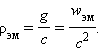
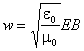 .
.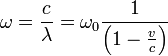 .
.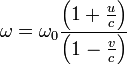 .
.