
- •2.Билет
- •3.Билет
- •4.Билет.
- •5 Билет.
- •6.Билет
- •7.Билет
- •8.Билет
- •10 Билет
- •11.Билет
- •12 Билет
- •13 Билет
- •14 Билет
- •15 Билет
- •16Билет
- •17.Билет
- •18.Билет
- •19.Билет
- •20.Билет
- •21Билет
- •22Билет
- •23 Билет
- •25 Билет
- •26 Билет
- •28.Билет
- •29 Билет
- •41. Вихревое электрическое поле
- •42. Дифференциальная и интегральная формы уравнений Максвелла.
- •43. Колебательный процесс. Виды колебаний . Гармонические колебания и их параметры.
- •44. Дифференциальное уравнение гармонических колебаний. Энергия гарм.Колеб.
- •45.Линейный гармонический Осциллятор, Математический и физический маятники:
- •46.Сложение одинаково направленных гармонических колебаний, биения.
- •47.Сложение взаимно перпендикулярных колебаний. Фигуры Лиссажу. Физический смысл спектрального разложения.
- •48.Свободно затухающие колебания. Дифференциальное уравнение свободных затухающих колебаний
- •50 Вопрос
- •51 Вопрос
- •52 Вопрос
50 Вопрос
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ - колебания, происходящие под действием внешней переменной силы (вынуждающей силы). (Установившиеся вынужденные колебания происходят с частотой, равной частоте вынуждающей силы.)
Рассмотрим вынужденные колебания на примере реального (с трением) пружинного маятника. Будем отталкиваться от уравнения движения (второй закон Ньютона). При наличии дополнительной вынуждающей силы F(t) необходимо дописать ее в правую часть уравнения. В каноническом виде дифференциальное уравнение вынужденных механических колебаний имеет вид:
![]() Для пружинного
маятника:
Для пружинного
маятника:
![]() и
и
![]()
Для того, чтобы
возникли периодические колебания,
вынуждающая сила сама должна быть
периодической. Пусть
![]() (писать
здесь начальную фазу смысла нет, поскольку
нас будут интересовать только
установившиеся вынужденные колебания,
то есть "забывшие" свое начало).
- частота вынуждающей силы. Для нахождения
уравнения установившихся колебаний
необходимо найти решение дифференциального
уравнения:
(писать
здесь начальную фазу смысла нет, поскольку
нас будут интересовать только
установившиеся вынужденные колебания,
то есть "забывшие" свое начало).
- частота вынуждающей силы. Для нахождения
уравнения установившихся колебаний
необходимо найти решение дифференциального
уравнения:
![]() при
при
![]() .
.
Общее
решение этого неоднородного
дифференциального уравнения представляет
собой, как известно из теории
дифференциальных уравнений, сумму
общего решения однородного уравнения
и любого частного решения неоднородного.
Общее решение однородного уравнения
нам известно, это - уравнение затухающих
колебаний. Оно нас не интересует, так
как при
оно исчезает. В качестве частного решения
неоднородного уравнения выберем
очевидное - мы знаем, что вынужденные
установившиеся колебания совершаются
с частотой вынуждающей силы. Поэтому
нашим искомым решением будет являться:
![]()
где А - амплитуда вынужденных колебаний, ۪ - сдвиг фаз между смещением и приложенной силой.
Получившиеся колебания подчиняются закону синуса (или косинуса), то есть являются синусоидальными или гармоническими. Но это не свободные колебания в системе без трения; здесь вынуждающая сила постоянно поставляет энергию в систему, в точности компенсирующую потери на преодоление сил трения.
Для амплитуды и сдвига фаз получаются следующие выражения:
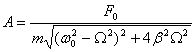 и
и
![]()
здесь - частота свободных (незатухающих) колебаний маятника; - коэффициент затухания.
Обратите
внимание, что амплитуда вынужденных
колебаний зависит от соотношения частоты
вынуждающей силы и собственной частоты
маятника. Максимальное значение амплитуды
получается, если
![]()
Частота
![]() называется
резонансной частотой, а достижение
максимума амплитуды колебаний при
изменении частоты называется явлением
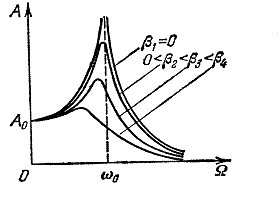
резонанса. График зависимости А() носит
название резонансной кривой. Обратите
внимание, что резонансная частота
механических колебаний зависит от
коэффициента затухания (а с ним и от
коэффициента силы трения). Если силы
трения отсутствуют, амплитуда колебаний
стремится к бесконечности.
называется
резонансной частотой, а достижение
максимума амплитуды колебаний при
изменении частоты называется явлением
резонанса. График зависимости А() носит
название резонансной кривой. Обратите
внимание, что резонансная частота
механических колебаний зависит от
коэффициента затухания (а с ним и от
коэффициента силы трения). Если силы
трения отсутствуют, амплитуда колебаний
стремится к бесконечности.
 Помимо поведения
амплитуды при резонансной частоте
рассмотрим ещё два предельных случая:
Помимо поведения
амплитуды при резонансной частоте
рассмотрим ещё два предельных случая:
![]() и
и
![]()
В первом мы получим обычное статическое смещение маятника под действием постоянной силы F0 (статическое растяжение пружины):
![]()
Во втором случае амплитуда равна нулю: инерция маятника не может успевать реагировать на бесконечную частоту.
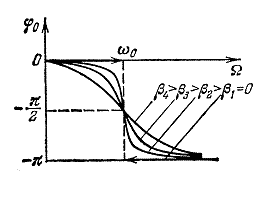
Зависимость сдвига фаз от соотношения частот представлена на рисунке. Сдвиг фаз между смещением и вынуждающей силой обусловлен инерцией маятника.
Амплитуда и фаза вынужденных колебаний. Резонанс
Рассмотрим зависимость амплитуды А вынужденных колебаний от частоты ω
(8.1)
Из формулы (8.1) следует, что амплитуда А смещения имеет максимум. Чтобы определить резонансную частоту ωрез — частоту, при которой амплитуда А смещения достигает максимума, — нужно найти максимум функции (1), или, что то же самое, минимум подкоренного выражения. Продифференцировав подкоренное выражение по ω и приравняв его нулю, получим условие, определяющее ωрез:
Это равенство выполняется при ω=0, ± , у которых только лишь положительное значение имеет физический смысл. Следовательно, резонансная частота
(8.2) (8.3)
Чем больше коэффициент затухания δ, тем ниже максимум резонансной кривой.
Явление раскачки колебаний под действием периодической внешней силы называется резонансом. Явления резонанса могут быть как вредными, так и полезными. Например, при конструировании машин и различного рода сооружений необходимо, чтобы собственная частота колебаний их не совпадала с частотой возможных внешних воздействий, в противном случае возникнут вибрации, которые могут вызвать серьезные разрушения. С другой стороны, наличие резонанса позволяет обнаружить даже очень слабые колебания, если их частота совпадает с частотой собственных колебаний прибора. Так, радиотехника, прикладная акустика, электротехника используют явление резонанса.
Следует подчеркнуть, что неограниченный резонансный рост амплитуды вынужденных колебаний есть идеализация системы. Во-первых, когда амплитуда колебаний становится достаточно большой, осциллятор, как правило, перестаёт быть линейным. Во-вторых, при записи уравнения (12) не учитывались силы трения, приводящие к затуханию колебаний. Рассмотрим роль последнего фактора более подробно.
Величину
![]() принято
называть шириной резонанса. При малых
принято
называть шириной резонанса. При малых
![]() эта
величина составляет
эта
величина составляет
![]() .
Тогда добротность, определяемая формулой
(8) пункта
2.3.2, связана с шириной
резонансной кривой соотношением
.
Тогда добротность, определяемая формулой
(8) пункта
2.3.2, связана с шириной
резонансной кривой соотношением
|
(13) |
Таким образом, ширина резонансной кривой определяется добротностью и собственной частотой. Чем больше добротность колебательной системы, тем меньше ширина резонансного пика. Как видно из формулы (13), добротность колебательной системы можно оценить из экспериментальных АЧХ осциллятора и соответственно определить коэффициент затухания.
Добро́тность — характеристика колебательной системы, определяющая полосу резонанса и показывающая, во сколько раз запасы энергии в системе больше, чем потери энергии за один период колебаний.
Добротность обратно пропорциональна скорости затухания собственных колебаний в системе. То есть, чем выше добротность колебательной системы, тем меньше потери энергии за каждый период и тем медленнее затухают колебания.
Общая формула для добротности любой колебательной системы:
![]() ,
где:
,
где:
![]() —
резонансная частота
колебаний
—
резонансная частота
колебаний
![]() —
энергия, запасённая
в колебательной системе
—
энергия, запасённая
в колебательной системе
![]() —
рассеиваемая мощность.
—
рассеиваемая мощность.
