Дифференциальное уравнение вынужденных колебаний (механических и электромагнитных) и его решение

Если рассматривать электрический колебательный контур, то роль X(t) играет подводимая к контуру внешняя периодически изменяющаяся по гармоническому закону э.д.с. или переменное напряжение

(147.3)

Тогда уравнение (143.2) с учетом (147.3) можно записать в виде

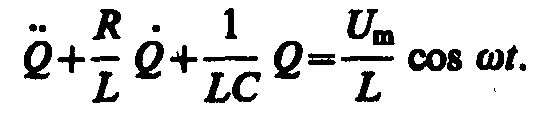
Используя (143.4) и (146.11), придем к уравнению

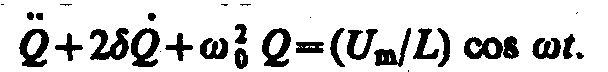(147.4)

Колебания, возникающие под действием внешней периодически изменяющейся силы или внешней периодически изменяющейся э.д.с., называются соответственно вынужденными механическими и вынужденными электромагнитными колебаниями.

Уравнения (147.2) и (147.4) можно свести к линейному неоднородному дифференци­альному уравнению

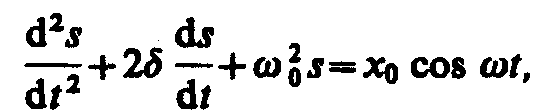(147.5)

применяя впоследствии его решение для вынужденных колебаний конкретной физичес­кой природы (x₀ в случае механических колебаний равно F₀/m, в случае электромагнит­ных — U_m/L).

Амплитуда и фаза вынужденных колебаний (механических и электромагнитных). Резонанс

Рассмотрим зависимость амплитуды А вынужденных колебаний от частоты . Меха­нические и электромагнитные колебания будем рассматривать одновременно, называя колеблющуюся величину либо смещением (х) колеблющегося тела из положения равновесия, либо зарядом (Q) конденсатора.

Из формулы (147.8) следует, что амплитуда А смещения (заряда) имеет максимум. Чтобы определить резонансную частоту _рез, — частоту, при которой амплитуда А сме­щения (заряда) достигает максимума, — нужно найти максимум функции (147.8), или, что то же самое, минимум подкоренного выражения. Продифференцировав подкорен­ное выражение по  и приравняв его нулю, получим условие, определяющее _рез :

Это равенство выполняется при =0, ± , у которых только лишь положи­тельное значение имеет физический смысл. Следовательно, резонансная частота (148.1)

Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы (частоты вынуждающего переменного напряжения) к ча­стоте, равной или близкой собственной частоте колебательной системы, называется резонансом (соответственно механическим или электрическим). При значение _рез практически совпадает с собственной частотой ₀ колебательной системы. Подста­вляя (148.1) в формулу (147.8), получим

(148.2) Из (148.1) и (148.2) вытекает, что чем меньше , тем выше и правее лежит максимум данной кривой. Если  0, то все кривые (см. также (147.8)) достигают одного в того же, отличного от нуля, предельного значения , которое называют статическим отклонением. В случае механических колебаний , в случае электромагнитных – U_m/(L ). Если , то вое кривые асимптотически стремятся к нулю. Приведенная совокупность кривых называется резонансными кривыми. Из формулы (148.2) вытекает, что при малом затухании ( ) резонансная амплитуда смещения (заряда) где Q — добротность колебательной системы (см. (146.8)), — рассмотренное выше статическое отклонение. Отсюда следует, что добротность Q характеризует резонансные свойства колебательной системы: чем больше Q, тем больше А_рез.

На рис. 211 представлены резонансные кривые для амплитуды скорости (тока). Амплитуда скорости (тока) максимальна при _рез=₀ и равна , т. е. чем больше коэффициент затухания , тем ниже максимум резонансной кривой. Используя формулы (142.2), (146.10) и (143.4), (146.11), получим, что амплитуда скорости при механическом резонансе равна

а амплитуда тока при электрическом резонансе

Из выражения tg = (см. (147.9)) следует, что если затухание в системе отсутствует (=0), то только в этом случае колебания и вынуждающая сила (прило­женное переменное напряжение) имеют одинаковые фазы; во всех других случаях  0.

Зависимость  от  при разных коэффициентах  графически представлена на рис. 212, из которого следует, что при изменении  изменяется и сдвиг фаз . Из формулы (147.9) вытекает, что при =0 =0, а при =₀ независимо от значения коэффициента затухания  = /2, т. е. сила (напряжение) опережает по фазе колебания на /2. При дальнейшем увеличении  сдвиг фаз возрастает и при >>₀   , т. е. фаза колебаний почти противоположна фазе внешней силы (переменного напряжения). Семейство кривых, изображенных на рис. 212, называется фазовыми резонансными кривыми.

Волна́ — изменение состояния среды или физического поля (возмущение), распространяющееся либо колеблющееся в пространстве и времени или в фазовом пространстве. Продольные волны (волны сжатия, P-волны) — частицы среды колеблются параллельно (по) направлению распространения волны (как, например, в случае распространения звука).

Поперечные волны (волны сдвига, S-волны) — частицы среды колеблются перпендикулярно направлению распространения волны (электромагнитные волны, волны на поверхностях разделения сред)

ФРОНТ ВОЛНЫ - поверхность, окружающая источник колебаний, все точки которой имеют одинаковые фазы колебаний. Фронт волны может быть сферой (сферическая волна) или иметь более сложную форму. Направление распространения волны - нормаль к фронту волны.

Длина́ волны́ — расстояние между двумя ближайшими друг к другу точками, колеблющимися в одинаковых фазах, обычно длина волны обозначается греческой буквой . По аналогии с возникающими волнами в воде от брошенного в неё камня — расстояние между двумя соседними гребнями волны. Одна из основных характеристик колебаний. Измеряется в единицах расстояния (метры, сантиметры и т. п.). Величина , обратная длине волны, называется волновым числом и имеет смысл пространственной частоты.

Волновая поверхность — геометрическое место точек, испытывающих возмущение обобщенной координаты в одинаковой фазе. Если источником волны является точка, то волновые поверхности в однородном и изотропном пространстве представляют собой концентрические сферы.

плоская волна — плоскости равных фаз перпендикулярны направлению распространения волны и параллельны друг другу;

сферическая волна — поверхностью равных фаз является сфера;

цилиндрическая волна — поверхность фаз напоминает цилиндр.

Базовым представителем волн являются линейные распространяющиеся волны, возникающие в системах, динамика которых может быть описана линейными гиперболическими уравнениями второго порядка (волновыми уравнениями) относительно характеристик системы .

где матрицы положительно определены для всех .

Гармоническая волна Гармонической волной называется линейная монохроматическая волна, распространяющаяся в бесконечной динамической системе. В распределённых системах общий вид волны описывается выражением, являющимся аналитическим решением линейного волнового уравнения

где – некоторая постоянная амплитуда волнового процесса, определяемая параметрами системы, частотой колебаний и амплитудой возмущающей силы; – круговая частота волнового процесса, – период гармонической волны, – частота; – волновое число, – длина волны, – скорость распространения волны; – начальная фаза волнового процесса, определяемая в гармонической волне закономерностью воздействия внешнего возмущения.

Если искать решение для гармонической волны путём предельного перехода от соответствующих решений для динамических систем с сосредоточенными параметрами, то указанное выражение существенно уточнится, выявив связь, заложенную в амплитуду . Это решение для амплитуды имеет вид ,где – амплитуда воздействующей силы , – плотность распределённой упругой системы, – в данном случае, жёсткость линии с распределёнными параметрами.

Волново́е число́ (также называемое пространственной частотой) — это отношение 2π радиан к длине волны: пространственный аналог круговой частоты.

Волновой вектор — вектор, направление которого перпендикулярно фазовому фронту бегущей волны, а абсолютное значение равно волновому числу.

Уравнением волны называется функция координат и времени, определяющая смещение точек среды из положения равновесия в любой момент времени во всём пространстве.

Уравнение плоской волны , – волновое число.

Волновое уравнение

Уравнение любой волны есть решение некоторого дифференциального уравнения, называемого волновым. Исходя из физических свойств среды и основных законов механики мы получаем волновое уравнение из явного выражения для уравнения плоской волны.

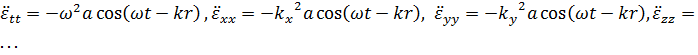. Можно записать : – волновое уравнение. Волновому уравнению будет удовлетворять любая волна произвольной частоты , распространяющаяся со скоростью . определяется физическими свойствами среды. В случае плоской волны, распространяющейся в направлении по х, волновое уравнение записывается в виде: .

Интерференция волн — взаимное усиление или ослабление амплитуды двух или нескольких когерентных волн, одновременно распространяющихся в пространстве.[1] Сопровождается чередованием максимумов и минимумов (пучностей) интенсивности в пространстве. Результат интерференции (интерференционная картина) зависит от разности фаз накладывающихся волн.

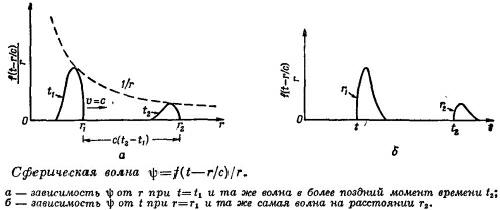
СФЕРИЧЕСКАЯ ВОЛНА - волна, радиально расходящаяся от нек-рой точки (источника) или сходящаяся к ней (к стоку) и имеющая сферич. волновые фронты (поверхности равных фаз). Простейшим примером является сферически симметричная скалярная волна вида

расходящаяся от центр. точки r = 0 (знак " -") или сходящаяся к ней (знак "+") со скоростью с. Такая волна удовлетворяет волновому уравнению и описывает многие физ. процессы в линейных средах без дисперсии и без потерь. Суперпозиция сходящейся и расходящейся волн (в частности, стоячая С. в.) также является решением волнового ур-ния.

Уравнение стоячей волны Очень важный случай интерференции наблюдается при наложении двух встречных плоских волн с одинаковой амплитудой. Стоячая волна это возникающий в результате колебательный процесс. Практически стоячие волны возникают при отражении волн от преград. Падающая на преграду волна и бегущая ей навстречу отраженная волна, налагаясь друг на друга, дают стоячую волну. Напишем уравнения двух плоских волн, распространяющихся вдоль оси х в противоположных направлениях:

Сложив вместе эти уравнения и преобразовав результат по формуле для суммы косинусов, получим уравнение стоячей волны:

Преобразовав это уравнение, получим упрощенное уравнение стоячей волны:

Стоячая волна не переносит энергию, так как падающая и отраженная волны имеют одинаковую амплитуду и несут одинаковую энергию в противоположных направлениях.

При наложении когерентных волн наблюдается их интерференция, т.е. усиление в одних точках пространства и ослабление в других. Важным случаем интерференции является наложение 2-ух встречных волн (одна из них может быть отражённой волной). В этом случае возникают стоячие волны. Запишем уравнения 2-ух плоских волн, распространяющихся вдоль ОХ в противоположном направлении, и сложим их: . Таким образом, в каждой точке пространства совершаются гармонические колебания частоты . Амплитуда этих колебаний меняется от 0 до по закону . Точки, в которых амплитуда достигает максимальной величины, называются пучностями стоячей волны, их координаты: . Точки, где амплитуда обращается в 0, называются узлами стоячей волны, их координаты: . Расстояние между соседними пучностями (узлами) равно половине длины волны.

Упру́гие во́лны (звуковые волны) — волны, распространяющиеся в жидких, твёрдых и газообразных средах за счёт действия упругих сил.

Упругая деформация — деформация, исчезающая после прекращения действий внешних сил. При этом тело принимает первоначальные размеры и форму.